上に述べたように,(標準)正規分布のグラフとx軸とで囲まれた図形の面積は,筆算で求めることはできませんので,あらかじめコンピュータを使って数値積分として求めた正規分布表を見て答えるようになっています.
正規分布表は次の1で示すような表です.
数学や統計の教科書は印刷物なので,上に示したような正規分布表を使って読者が目で追って求めるしかありませんが,この教材(あなたが見ているこの頁)はコンピュータ上に表示されていますので,上記のようなuを書き込んだら対応する確率Pをコンピュータに探させることは簡単にできます.
次の2は,上と同じ正規分布表で,変数uを入力したら確率Pを返すものです.
4【Excelで計算する場合】

○ Excelの表計算関数では,標準正規分布関数として =NORMSDIST(u) が利用できますが,この関数は右図のように
P(−∞<z<u)の値を表しているので,正規分布表に書かれている
P(0<z<u)の値に直すためには,左半分の面積
P(z<0)すなわち
0.5もしくは=NORMSDIST(0)を引きます.
例えば,
P(0<z<1)の値は,=NORMSDIST(1)−0.5で得られます.
【例1】
=NORMSDIST(1) とすると0.8413が返されますが,上の図で水色の部分の面積は左半分の面積0.5も含んでいるため,P(0<z<1)の値を求めるためには0.8413−0.5=0.3413としなければなりません.
この関数は負の数に対しても利用でき,
a<bのとき
P(a<z<b)の値は=NORMSDIST(b)−NORMSDIST(a)で求められます.
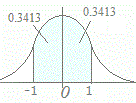 【例2】
【例2】
=NORMSDIST(1)-NORMSDIST(-1) とすると
0.6827が返されます.これは右図の面積を表しています.(小数第4位は下位の桁の計算の結果として繰り上がりがあります)
○ Excelで一般の正規分布(期待値0,標準偏差1とは限らない場合)の確率を計算するには,関数
NORMDIST(xの値 , 期待値 , 標準偏差 , 1)
が使えます.上の図のような確率(曲線の下にある図形の面積)を求めるには,4番目の数字に
1または TRUE を代入します.(確率密度関数の値 [グラフのy座標=縦線の長さ]を求めるときには,4番目の数字に0またはFALSEを代入します.)
なお,引数の順序に注意.また,
第3引数が分散ではなく標準偏差であることにも注意
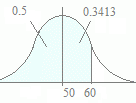 【例3】
【例3】
=NORMDIST(
60 ,
50 ,
10 ,1) とすると
0.8413が返されます.
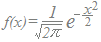
 ○ P(a<z<b)という記号によって,a<z<bとなる確率を表します.
○ P(a<z<b)という記号によって,a<z<bとなる確率を表します. ○ 曲線の下にある図形の面積全部で確率1を表しますが,グラフが左右対称になっているので,右半分,左半分の面積はそれぞれ0.5になります.
○ 曲線の下にある図形の面積全部で確率1を表しますが,グラフが左右対称になっているので,右半分,左半分の面積はそれぞれ0.5になります. 2【標準正規分布の累積関数】
2【標準正規分布の累積関数】
 ○ Excelの表計算関数では,標準正規分布関数として =NORMSDIST(u) が利用できますが,この関数は右図のように
○ Excelの表計算関数では,標準正規分布関数として =NORMSDIST(u) が利用できますが,この関数は右図のように 【例2】
【例2】 【例3】
【例3】
 (解答)
(解答) (解答)
(解答)