 ■ 解説
■ 解説小学校以来,右図のように,角度は分度器を用いて測り,0°〜360°までとしてきた. さらに進んだ数学を学ぶためには,負の角や360°よりも大きい角度まで角度の範囲を広げて考える.このように意味を広げて拡張した角度を一般角という. 一般角は,x軸の正の向きOXを始線(0°)として,動径OP(動く半径という意味)を回転させて考え,
「反時計回り=左回り」を正の向き
と決める.(これは世界共通の約束事なので「なぜ」と尋ねても無駄)
「時計回り=右回り」を負の向き このように,一般角は動径(動く半径)を用いて表わす. 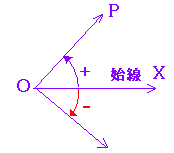
例
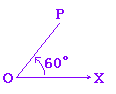 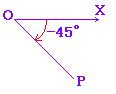 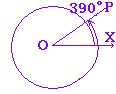
|