← PC用は別頁

== 度数分布表から平均値，分散，標準偏差を求める ==
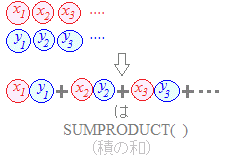
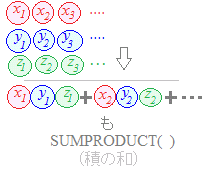
（Excelの利用）
○［平均値x］
　n個のデータx1 , x2 , x3 , ..., xnの平均値xは，値の合計T=x1+x2+x3+...+xnを，個数の合計nで割ったものとして定義されます．
.x=(x1+x2+x3+...+xn )
※［度数分布表から平均値を求めるには］
表１
以上 未満 階級値 度数
x1 x2 m1 f1
x2 x3 m2 f2
x3 x4 m3 f3
… … … …
… … … …
　表１のように，データが度数分布表で与えられている場合には，例えばx1以上x2未満の階級にf1個のデータがあるのだから，この区間の中央
.m1=
にf1個のデータがあるとみなせます．
　同様にして，x2以上x3未満の階級にf2個のデータがあるのだから，この区間の中央
.m2=
にf2個のデータがあるとみなせます．
　この結果，平均値は次の式で求められます．
.x=(m1+m1+...m2+m2+...+... )

f1個f2個
したがって
.x=(m1 f1+m2 f2+... ) …(1)
（ただしf1+f2+...=n）
【例】
表２
以上 未満 階級値xk 度数fk 仮変数uk
30 35 32.5 3 -2
35 40 37.5 5 -1
40 45 42.5 7 0
45 50 47.5 4 1
50 55 52.5 1 2
　表２の場合，データ総数はn=3+5+7+...=20だから
.x=(32.5×3+37.5×5+42.5×7+... )=41.25
となります．


※［仮平均を使った簡便計算法によって平均値を求めるには］
　今日では，平均値，分散，標準偏差はコンピュータを使って求めることが多く，左記の(1)によって直接求めると簡単に求まります．だから，コンピュータで処理する場合には，以下で述べる簡便計算法は必要ありません．
　ここで解説する仮平均を使った簡便計算法は，筆算で１桁程度の数値の掛け算や足し算で求めたい場合に適しています．
（やり方）
　度数分布表の中央付近で，度数の最も大きい階級（表２では，赤で示した42.5）の階級値を0として，増える方向に1, 2, ..，減る方向に−1, −2, ..という階級値を仮変数として割り当てます．
　この仮変数uを階級値の代わりに使って平均値を求めると，
.u=((−2)×3+(−1)×5+0×7+...)=−0.25
　度数の最も大きい階級の階級値としての仮変数を0にすることの長所は，大きな度数でも0を掛けることになって，計算が省略できるからです．（上記の計算中の0×7）
　度数分布表の中央付近で，仮変数0にすると大きい方も小さい方も±2のように小さな整数値になって，計算が楽になるからです．先頭を0から始めて（仮平均を他の値に設定しても，例えば32.5としても）も正しく求めることはできますが，階級値の仮変数として，0,1,2,3,4などとすると数字が大きくなる分だけ不利です．
　このようにして仮変数で求めた平均値uは，そのままでは本来求めるべき平均値とは異なっていますが，次のように元の変数に戻すことができます．
.u=　⇔　x=42.5+5u
したがって
.x=42.5+5 =42.5+5×(−0.25)=41.25

　一般に，階級幅cの度数分布表において，仮平均をx0として仮変数uを導入するとき，元の変数xを用いた計算が複雑な小数計算であっても，uを用いた計算は，階級幅1の簡単な整数値の計算でできます．
　このとき，uからxへは次の式で戻すことができます．
.x=x0+cu …(*1)
　標準偏差s:suは，階級幅c:1に比例します．
s=csu …(*2)
　分散は標準偏差の２乗です．
V=s2=c2su2 …(*3)
※変数変換に伴う平均値，分散，標準偏差の変換の詳細は，この頁

［分散Vまたはs2，標準偏差s］
　分散は，平均値からの偏差xi−xの２乗の平均として定義されます．
.V={ (x1−x)2+(x2−x)2+... }
　標準偏差は，上記の分散の正の平方根として定義されます．
.s=
※［度数分布表から分散を求めるには］
　次の表１のようにデータが度数分布表で与えられている場合には，この場合も(m1−x)2がf1個，(m2−x)2がf2個，...と考えると
.V={ (m1−x)2 f1+(m2−x)2 f2+ ...... } …(3)
この分散は
.V=(m12 f1+m22 f2 ... )−x2 …(4)
すなわち
（分散）＝（２乗の平均）−（平均の２乗）
と書き直すことができます．
　(3)と(4)のどちらを使えばよいのか？
　今日では，統計処理をコンピュータで行うことが多いので，(3)でやれば十分です．(4)式は小数計算の計算量をなるべく少なくしたいときに（例えば，筆算で行うときなどに）適していますので，(4)でやらなければならないということはありません．
　ただし，コンピュータで計算する場合でも，計算式の範囲指定がズレてしまうなどのうっかりミスを防ぐためには，２種類以上の計算方法で求めて，それらが一致するかどうか確かめるようにする方がよく，２通りの方法で計算して突き合わせることには意義があります．
【例】
(3)→
次の表３の場合
○ =SUM(D2:D8) により，データの個数n=970が求まります．（これをセルD9に書きこむものとする．7.74）
○ 平均値は，（階級値）×（度数）の和をデータの個数で割って求めます．
　階級値×度数は，例えばセルE2に =C2*D2 として，これを下方にコピー&貼り付けしてもできますが，=SUMPRODUCT()を使う方法があります．
=SUMPRODUCT()は数学の内積に相当します．
=SUMPRODUCT(C2:C8,D2:D8)/［データの個数］により，平均値が求まります．
○ (3)式による分散は，例えばセルC9に上記の平均値を記入している場合，まずE列に偏差を準備しておくことから始める．
セルE2に =C2−$C$9　←C9の方は絶対参照にします
これをコピーして，E3からE8に貼り付け
たとえば，セルE3には =C3−$C$9　という式が貼り付けられる．
(3)式を計算するためには，各々の偏差の２乗×度数を求めから，それらの和を計算してもよいが，ワークシート関数 SUMPRODUCT()を利用するとよい．
　次図１，２の要領でE列，E列，D列の積の和を求めるとよいから
=SUMPRODUCT(E2:E8, E2:E8, D2:D8)
これをセルD9に計算してあるデータの個数で割ると分散になります．
=SUMPRODUCT(E2:E8, E2:E8, D2:D8)/D9 →0.0468
(4)→
○ =SUMPRODUCT(C2:C8, C2:C8, D2:D8)/D9-C9^2により（２乗の平均）−（平均の２乗）が求められます． →0.0468
(3)(4)の２つの方法で求めた分散が一致するのでこれを使用する．
○ 標準偏差は =SQRT(分散)にｙり求めます． →0.21


※Excelで計算すると，平均値，分散，標準偏差などは，セル幅が広ければ小数第７位，８位などと表示されますが，どこまで使えばよいのか．
→２，３個の数値の和差積商では，元の数の有効数字に合わせます（［例」３桁×３桁なら３桁で答える），が多数のデータ（例えば10件以上）から平均値，分散，標準偏差を求めるときは，概ね次のように処理されていることが多いようです．（途中経過はコンピュータまかせにして（特に丸めることはせずに），結果の桁数だけを丸める．）
*　平均値の有効数字は，元の観測値よりも１桁増やす．
*　標準偏差の有効数字は平均値の有効数字に合わせる．
*　分散の有効数字は標準偏差の２倍にする．（ルートが標準偏差の桁数になるようにする）
［例］
階級値：3.02, 2.98, 3.50, ... （数十件あるとする）→小数第２位まで
⇒ 平均値：3.243 ←小数第３位まで
⇒ 分散：0.178929←小数第６位まで
↑ 標準偏差：0.423←小数第３位まで
再掲：表１
以上 未満 階級値 度数
x1 x2 m1 f1
x2 x3 m2 f2
x3 x4 m3 f3
… … … …
… … … …
(4)の証明
V={ (m1−x)2 f1+(m2−x)2 f2+ ...... }
={ (m12 −2m1x+x2 )f1
+(m22 −2m2x+x2 )f2
+ ...... }
=(m12 f1+m22 f2+ ... )
−(m1f1+m2f2+ ... ) x
+(f1+f2+ ... ) x2
ここで
(m1 f1+m2 f2+... )=x，f1+f2+...=n
だから
V=(m12 f1+m22 f2+ ... )−2x2+x2
=(m12 f1+m22 f2+ ... )−x2

表３
　 A B C D E
1 以上 未満 階級値 度数 偏差
2 7.1 7.3 7.2 17 　
3 7.3 7.5 7.4 91 　
4 7.5 7.7 7.6 299 　
5 7.7 7.9 7.8 352 　
6 7.9 8.1 8 156 　
7 8.1 8.3 8.2 52 　
8 8.3 8.5 8.4 3 　
図１
表４
　 A B C
1 -2 5 6
2 3 1 -2
3 1 -2 1
4 4 3 2
［例］
=SUMPRODUCT(A1:C1, A2:C2)は行ベクトルと行ベクトルの内積
−2*3+5*1+6*(−2)=−13
=SUMPRODUCT(B1:B4, C1:C4)は列ベクトルと列ベクトルの内積
5*6+1*(−2)+(−2)*1+3*2=32
図２
［例］
　数学では，３つのベクトルの内積？などは聞かないが，コンピュータでは「３つの配列の積の和」「４つの配列の積の和」でも自由にできます．
　上記の表４において
=SUMPRODUCT(A1:C1, A2:C2, A3:C3)とすれば
−2*3*1+5*1*(−2)+6*(−2)*1=−28
※「行の配列」と「列の配列」の積の和は，=SUMPRODUCT()ではなく，行列の積 =MMULT()で求めます．

　次の表５は，1951年から2012年までの62年間に，日本に上陸した台風の１年間の上陸数とその度数一覧です．（例えば，赤で示した数字は，１年間に３個上陸した年が18年あることを示しています．）
表５
上陸数 度数
0 4
1 7
2 16
3 18
4 9
5 5
6 2
7 0
8 0
9 0
10 1

元のデータは，気象庁 台風の上陸数http://www.data.jma.go.jp/fcd/ yoho/typhoon/statistics/landing/landing.html
平たく言えば，１年間に日本に台風が上陸した回数のことですが，おそらく１つの台風が２回以上上陸している場合もあるので，１年間に日本に上陸した台風の個数ということになる．
この表は，気象庁のデータから度数分布表を作成したもの．
画面上でドラッグ・コピーしてExcel上に単純に貼り付けるて利用すればよい．
　正しい番号を選択してください．
［問題１］
この期間について，年間上陸数の平均値は次のうちどれですか．

12.5 22.8 33.1 43.4 53.7



［問題２］
この期間の年間上陸数の分散を求めてください．

12.48 22.59 32.70 42.81 52.92



［問題３］
この期間の年間上陸数の標準偏差を求めてください．

11.7 21.8 31.9 42.0 52.1




次の表６はある日１日に釣り上げられた魚の重さ別一覧だとします．（架空データ）
このデータについて，以下の問いに答えてください．
表６
魚の重さ(kg) 度数
以上 未満
1.0 1.1 1
1.1 1.2 1
1.2 1.3 2
1.3 1.4 3
1.4 1.5 5
1.5 1.6 6
1.6 1.7 4
1.7 1.8 3
1.8 1.9 2
1.9 2.0 2
2.0 2.1 1
計 30
［問題４］
魚の重さ（kg）の平均値を求めてください.

11.42 21.45 31.48 41.53 51.56



［問題５］
魚の重さ(kg)の分散を求めてください．

10.0478 20.0556 30.0612

40.0723 50.0815


［問題６］
魚の重さ(kg)の標準偏差を求めてください

10.24 20.25 30.26 40.27 50.28




次の表７は生徒20人の身長を集計したものとします．（架空データ）
この度数分布表から，仮平均を用いた簡便計算法により平均値，分散，標準偏差を求めるとき，次の問いに答えてください．
表７
身長(cm) 階級値 度数 仮変数
以上 未満 f u
150 155 152.5 3 -2
155 160 157.5 5 -1
160 165 162.5 7 0
165 170 167.5 4 1
170 175 172.5 1 2
計 20 　
［問題７］
次の表では，仮平均x0を何cmとして計算していることになりますか．

1155 2157.5 3160 4162.5 5165



［問題８］
仮変数uで表したときの平均値uはいくらになりますか．

1−0.5 2−0.25 30 40.25 50.5


［問題９］
仮変数uで表したときの標準偏差suはいくらになりますか．

11.09 21.19 34.09 44.19 54.99



［問題10］
生徒の身長の平均値と標準偏差は各々いくらになりますか．

1平均−0.25，標準偏差1.1875

2平均−0.25，標準偏差1.09

3平均−0.25，標準偏差5.45

4平均161.25，標準偏差29.6875

5平均161.25，標準偏差5.45




（携帯版）統計メニューに戻る

...メニューに戻る