三角形の証明問題と形状問題

== 三角形の証明問題と形状問題(よく出るもの) ==

証明問題

数学Ⅰの正弦定理で解けるもの

■「次の等式を証明せよ」という問題の場合■
$a(\sin B+ \sin C)=(b+ c)\sin A$ …(1.1)
$(a-b)\sin C+ (b-c)\sin A+ (c-a)\sin B=0$ …(1.2)
$c(\sin^2 A+\sin^2 B)=\sin C(a\sin A+ b\sin B)$ …(1.3)

（解説）

三角関数を使った式，例えばsinAsin(B+C)は一般に変形しにくく，辺を使った式，例えばa(b+c)は展開しやすいので，なるべく辺だけで表すようにします．
ここでは，正弦定理 $\frac{a}{\sin A}=2R$ を変形して $\sin A=\frac{a}{2R}$ として使うとよいでしょう．sinB, sinCも同様です．
このとき，一時的に外接円の半径Rが登場しますが，両辺や分母・分子に対等に表れるので，問題ありません．

※以下において，式(m.n)←という記号は，式(m.n)の証明という意味です

(1.1)←
$\sin A=\frac{a}{2R},\hspace{5}\sin B=\frac{b}{2R},\hspace{5}\sin C=\frac{c}{2R}$ を代入すると
（左辺）＝ $a(\frac{b}{2R}+\frac{c}{2R})=\frac{a(b+ c)}{2R}$
（右辺）＝ $(b+ c)\frac{a}{2R}=\frac{a(b+ c)}{2R}$
よって，等式(1.1)が成り立つ

(1.2)←
$\sin A=\frac{a}{2R},\hspace{5}\sin B=\frac{b}{2R},\hspace{5}\sin C=\frac{c}{2R}$ を代入すると
（左辺）＝ $(a-b)\frac{c}{2R}+ (b-c)\frac{a}{2R}+ (c-a)\frac{b}{2R}$
$=\frac{1}{2R}(ac-bc+ ab-ac+ bc-ab)=0$
よって，等式(1.2)が成り立つ

(1.3)←
$\sin A=\frac{a}{2R},\hspace{5}\sin B=\frac{b}{2R},\hspace{5}\sin C=\frac{c}{2R}$ を代入すると
（左辺）＝ $c(\sin^2 A+\sin^2 B)=c(\frac{a^2}{4R^2}+\frac{b^2}{4R^2})$
$=\frac{c(a^2+ b^2)}{4R^2}$
（右辺）＝ $\frac{c}{2R}(a\frac{a}{2R}+ b\frac{b}{2R})=\frac{c(a^2+ b^2)}{4R^2}$
よって，等式(1.3)が成り立つ

数学Ⅰの余弦定理で解けるもの

■「次の等式を証明せよ」という問題の場合■
$a^2+ b^2+ c^2=2(bc\cos A+ ca\cos B+ ab\cos C)$ …(2.1)
$a(b\cos C-c\cos B)=b^2-c^2$ …(2.2)
$\frac{\cos A}{a}+\frac{\cos B}{b}+\frac{\cos C}{c}=\frac{a^2+ b^2+ c^2}{2abc}$ …(2.3)
$a(\cos B-\cos C)=(c-b)(1+ \cos A)$ …(2.4)

三角関数を使った式，例えばcosAcos(B+C)は一般に変形しにくく，辺を使った式，例えばa(b+c)は展開しやすいので，なるべく辺だけで表すようにします．
ここでは，余弦定理 $a^2=b^2+ c^2-2bc\cos A$ を変形して $\cos A=\frac{b^2+ c^2-a^2}{2bc}$ として使うとよいでしょう．cosB, cosCも同様です．

（解説）
(2.1)←
$\cos A=\frac{b^2+ c^2-a^2}{2bc},\hspace{5}\cos B=\frac{c^2+ a^2-b^2}{2ca}$
$\cos C=\frac{a^2+ b^2-c^2}{2ab}$ を代入すると
（右辺）
$=2(bc\frac{b^2+ c^2-a^2}{2bc}+ ca\frac{c^2+ a^2-b^2}{2ca}+ ab\frac{a^2+ b^2-c^2}{2ab})$
$=b^2+ c^2-a^2+c^2+ a^2-b^2+ a^2+ b^2-c^2$
$=a^2+ b^2+ c^2=$ （左辺）
よって等式(2.1)が成り立つ

(2.2)←
$\cos A=\frac{b^2+ c^2-a^2}{2bc},\hspace{5}\cos B=\frac{c^2+ a^2-b^2}{2ca}$
$\cos C=\frac{a^2+ b^2-c^2}{2ab}$ を代入すると
（左辺） $=a(b\frac{a^2+ b^2-c^2}{2ab}-c\frac{c^2+ a^2-b^2}{2ca})$
$=\frac{a^2+ b^2-c^2-c^2-a^2+ b^2}{2}=b^2-c^2=$ （右辺）
よって等式(2.2)が成り立つ

(2.3)←
$\cos A=\frac{b^2+ c^2-a^2}{2bc},\hspace{5}\cos B=\frac{c^2+ a^2-b^2}{2ca}$
$\cos C=\frac{a^2+ b^2-c^2}{2ab}$ を代入すると
（左辺）
$=\frac{\frac{b^2+ c^2-a^2}{2bc}}{a}+\frac{\frac{c^2+ a^2-b^2}{2ca}}{b}+\frac{\frac{a^2+ b^2-c^2}{2ab}}{c}$
$=\frac{b^2+ c^2-a^2+ c^2+ a^2-b^2+ a^2+ b^2-c^2}{2abc}$
$=\frac{a^2+ b^2+ c^2}{2abc}=$ （右辺）
よって等式(2.3)が成り立つ

(2.4)←
$\cos A=\frac{b^2+ c^2-a^2}{2bc},\hspace{5}\cos B=\frac{c^2+ a^2-b^2}{2ca}$
$\cos C=\frac{a^2+ b^2-c^2}{2ab}$ を代入すると
（左辺）＝ $a(\cos B-\cos C)$
$=a(\frac{c^2+ a^2-b^2}{2ca}-\frac{a^2+ b^2-c^2}{2ab})$
$=\frac{c^2+ a^2-b^2}{2c}-\frac{a^2+ b^2-c^2}{2b}$
$=\frac{bc^2+ a^2b-b^3-a^2c-b^2c+ c^3}{2bc}$
$=\frac{1}{2bc}\{(a^2b-a^2c)+(bc^2-b^3-b^2c+ c^3)\}$
$=\frac{1}{2bc}\{a^2(b-c)+(bc^2+ c^3)-(b^3+ b^2c)\}$
$=\frac{1}{2bc}\{a^2(b-c)+ c^2(b+ c)-b^2(b+ c)\}$
$=\frac{1}{2bc}\{a^2(b-c)+ (c^2-b^2)(b+ c)\}$
$=\frac{1}{2bc}\{a^2(b-c)+ (c-b)(b+ c)^2\}$
$=\frac{b-c}{2bc}\{a^2-(b+ c)^2\}$
$=\frac{(b-c)(a+ b+ c)(a-b-c)}{2bc}$
（右辺）＝ $(c-b)(1+ \frac{b^2+ c^2-a^2}{2bc})$
$=(c-b)\frac{2bc+ b^2+ c^2-a^2}{2bc}$
$=(c-b)\frac{(b+ c)^2-a^2}{2bc}$
$=\frac{(c-b)(a+ b+ c)(b+ c-a)}{2bc}$
よって等式(2.4)が成り立つ

数学Ⅰの正弦定理・余弦定理で解けるもの

■「次の等式を証明せよ」という問題の場合■
$\frac{a\sin C}{b-a\cos C}=\tan A$ …(3.1)
$\frac{a-c\cos B}{b-c\cos A}=\frac{\sin B}{\sin A}$ …(3.2)
$a\cos A\sin C=(b-a\cos C)\sin A$ …(3.3)
$\frac{\tan B}{\tan C}=\frac{a^2+ b^2-c^2}{a^2-b^2+ c^2}$ …(3.4)
$\frac{b^2-c^2}{\tan A}+\frac{c^2-a^2}{\tan B}+\frac{a^2-b^2}{\tan C}=0$ …(3.5)
$(-a^2+ b^2+ c^2)\tan A=(a^2-b^2+ c^2)\tan B$
$=(a^2+ b^2-c^2)\tan C$ …(3.6)

（解説）

$\sin A=\frac{a}{2R},\hspace{5}\cos A=\frac{b^2+ c^2-a^2}{2bc}$
などを用いて角度の式を辺の式に直すのが基本です．

(3.1)←
（左辺）＝ $\frac{a\frac{c}{2R}}{b-a\frac{a^2+ b^2-c^2}{2ab}}=\frac{\frac{ac}{2R}}{\frac{2b^2-a^2-b^2+ c^2}{2b}}$
$=\frac{ac}{2R}\cdot\frac{2b}{b^2-a^2+ c^2}=\frac{abc}{R(b^2+ c^2-a^2)}$
（右辺）＝ $\frac{\sin A}{\cos A}=\frac{\frac{a}{2R}}{\frac{b^2+ c^2-a^2}{2bc}}=\frac{a}{2R}\cdot\frac{2bc}{b^2+ c^2-a^2}$
$=\frac{abc}{R(b^2+ c^2-a^2)}$
よって等式(3.1)が成り立つ

(3.2)←
（左辺）＝ $\frac{a-c\frac{c^2+ a^2-b^2}{2ca}}{b-c\frac{b^2+ c^2-a^2}{2bc}}=\frac{\frac{2a^2-c^2-a^2+ b^2}{2a}}{\frac{2b^2-b^2-c^2+ a^2}{2b}}$
$=\frac{\frac{a^2+ b^2-c^2}{2a}}{\frac{a^2+ b^2-c^2}{2b}}=\frac{a^2+ b^2-c^2}{2a}\cdot\frac{2b}{a^2+ b^2-c^2}=\frac{b}{a}$
（右辺）＝ $\frac{\frac{b}{2R}}{\frac{a}{2R}}=\frac{b}{2R}\cdot \frac{2R}{a}=\frac{b}{a}$
よって等式(3.2)が成り立つ

(3.3)←
（左辺）＝ $a\frac{b^2+ c^2-a^2}{2bc}\cdot\frac{c}{2R}=\frac{a(b^2+ c^2-a^2)}{4Rb}$
（右辺）＝ $(b-a\frac{a^2+ b^2-c^2}{2ab})\frac{a}{2R}$
$=\frac{2b^2-a^2-b^2+ c^2}{2b}\cdot\frac{a}{2R}=\frac{a(b^2+ c^2-a^2)}{4Rb}$
よって等式(3.3)が成り立つ

(3.4)←
（左辺）＝ $\frac{\frac{\sin B}{\cos B}}{\frac{\sin C}{\cos C}}=\frac{\sin B}{\cos B}\cdot\frac{\cos C}{\sin C}$
$=\frac{\frac{b}{2R}}{\frac{c^2+ a^2-b^2}{2ca}}\cdot\frac{\frac{a^2+ b^2-c^2}{2ab}}{\frac{c}{2R}}$
$=\frac{b}{2R}\cdot\frac{2ca}{c^2+ a^2-b^2}\cdot\frac{a^2+ b^2-c^2}{2ab}\cdot\frac{2R}{c}=\frac{a^2+ b^2-c^2}{c^2+ a^2-b^2}$
＝（右辺）
よって等式(3.4)が成り立つ

(3.5)←
（左辺）＝ $\frac{b^2-c^2}{\frac{\sin A}{\cos A}}+\frac{c^2-a^2}{\frac{\sin B}{\cos B}}+\frac{a^2-b^2}{\frac{\sin C}{\cos C}}$
$=(b^2-c^2)\frac{\cos A}{\sin A}+ (c^2-a^2)\frac{\cos B}{\sin B}+ (a^2-b^2)\frac{\cos C}{\sin C}$
$=(b^2-c^2)\frac{\frac{b^2+ c^2-a^2}{2bc}}{\frac{a}{2R}}+(c^2-a^2)\frac{\frac{c^2+ a^2-b^2}{2ca}}{\frac{b}{2R}}$
$+(a^2-b^2)\frac{\frac{a^2+ b^2-c^2}{2ab}}{\frac{c}{2R}}$
$=\frac{2R(b^2-c^2)(b^2+ c^2-a^2)}{2abc}$
$+\frac{2R(c^2-a^2)(c^2+ a^2-b^2)}{2abc}$
$+\frac{2R(a^2-b^2)(a^2+ b^2-c^2)}{2abc}$
$=\frac{R}{abc}\{(b^2-c^2)(b^2+ c^2-a^2)$
$+(c^2-a^2)(c^2+ a^2-b^2)$
$+(a^2-b^2)(a^2+ b^2-c^2)\}$
$=\frac{R}{abc}\{(b^2-c^2)(b^2+ c^2)-(b^2-c^2)a^2$
$+(c^2-a^2)(c^2+ a^2)-(c^2-a^2)b^2$
$+(a^2-b^2)(a^2+ b^2)-(a^2-b^2)c^2\}$
$=\frac{R}{abc}\{b^4-c^4-a^2b^2+ a^2c^2$
$+ c^4-a^4-b^2c^2+ a^2b^2$
$+ a^4-b^4-a^2c^2+ b^2c^2\}=0$
＝（右辺）
よって等式(3.5)が成り立つ

(3.6)←
（第１辺）＝ $(-a^2+ b^2+ c^2)\frac{\sin A}{\cos A}$
$=(-a^2+ b^2+ c^2)\frac{\frac{a}{2R}}{\frac{b^2+ c^2-a^2}{2bc}}$
$=(-a^2+ b^2+ c^2)\cdot\frac{a}{2R}\cdot\frac{2bc}{b^2+ c^2-a^2}=\frac{abc}{R}$
（第２辺）＝ $(a^2-b^2+ c^2)\frac{\sin B}{\cos B}$
$=(a^2-b^2+ c^2)\frac{\frac{b}{2R}}{\frac{c^2+ a^2-b^2}{2ca}}$
$=(a^2-b^2+ c^2)\cdot\frac{b}{2R}\cdot\frac{2ca}{c^2+ a^2-b^2}=\frac{abc}{R}$
（第３辺）＝ $(a^2+ b^2-c^2)\frac{\sin C}{\cos C}$
$=(a^2+ b^2-c^2)\frac{\frac{c}{2R}}{\frac{a^2+ b^2-c^2}{2ab}}$
$=(a^2+ b^2-c^2)\cdot\frac{c}{2R}\cdot\frac{2ab}{a^2+ b^2-c^2}=\frac{abc}{R}$
よって等式(3.6)が成り立つ

数学Ⅰで面積Sや内接円の半径rに関するもの

面積をS，外接円の半径をR，内接円の半径をr， $s=\frac{a+ b+ c}{2}$ で表すとき

■「次の等式を証明せよ」という問題の場合■
$S=2R^2\sin A\sin B\sin C$ …(4.1)
$S=\frac{1}{2}r(a+ b+ c)=rs$ …(4.2)
$S=Rr(\sin A+\sin B+\sin C)$ …(4.3)
$S=\frac{abc}{4R}$ …(4.4)
$abc=2(a+ b+ c)Rr$ …(4.5)
$\frac{1}{bc}+\frac{1}{ca}+\frac{1}{ab}=\frac{1}{2rR}$ …(4.6)
$\sin A+\sin B+\sin C=\frac{4sS}{abc}$ …(4.7)
$(b^2+ c^2-a^2)\tan A=4S$ …(4.8)
$\tan\frac{A}{2}=\frac{r}{s-a}$ …(4.9)
$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\underline{\ge}\frac{9}{2s}$ …(4.10)
$s^2\underline{\ge}3\sqrt{3}S$ …(4.11)

（解説）
(4.1)←
教科書に書かれている，次の公式は前提とします．
$S=\frac{1}{2}ab\sin C$
この式に，正弦定理から得られる $a=2R\sin A,\hspace{5}b=2R\sin B$ を代入すると
$S=\frac{1}{2}\times 2R\sin A\cdot2R\sin B\sin C$
$=2R^2\sin A\sin B\sin C$
よって等式(4.1)が成り立つ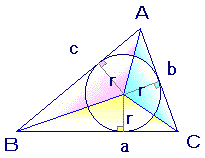

(4.2)←
右図のように三角形を３つに分けると
$S=\frac{1}{2}ra+\frac{1}{2}rb+\frac{1}{2}rc$
$=\frac{1}{2}r(a+ b+ c)=rs$
よって等式(4.2)が成り立つ

(4.3)←
(4.2)に，正弦定理から得られる $a=2R\sin A,\hspace{5}b=2R\sin B,\hspace{5}c=2R\sin C$ を代入すると
$S=\frac{1}{2}r(2R\sin A+ 2R\sin B+ 2R\sin C)$
$=Rr(\sin A+\sin B+ \sin C)$
よって等式(4.3)が成り立つ

(4.4)←
$S=\frac{1}{2}ab\sin C$
に，正弦定理から得られる $\sin C=\frac{c}{2R}$ を代入すると
$S=\frac{1}{2}ab\times\frac{c}{2R}=\frac{abc}{4R}$
よって等式(4.4)が成り立つ

(4.5)←
(4.2)と(4.4)から
$\frac{1}{2}r(a+ b+ c)=S=\frac{abc}{4R}$
分母を払うと
$2Rr(a+ b+ c)=abc$
よって等式(4.5)が成り立つ

(4.6)←
(4.5)の両辺を $2Rrabc$ で割ると
$\frac{1}{2Rr}=\frac{a+ b+ c}{abc}$
$\frac{1}{bc}+\frac{1}{ca}+\frac{1}{ab}=\frac{1}{2Rr}$
よって等式(4.6)が成り立つ

(4.7)←
(4.2)から
$a+ b+ c=\frac{2S}{r}$
この式に， $a=2R\sin A,\hspace{5}b=2R\sin B$ を代入すると
$2R\sin A+ 2R\sin B+ 2R\sin C=\frac{2S}{r}$
$\sin A+ \sin B+ \sin C=\frac{S}{Rr}$
(4.4)から
$R=\frac{abc}{4S}$
を代入すると
$\sin A+ \sin B+ \sin C=\frac{S}{\frac{abc}{4S}\cdot r}=\frac{4S^2}{abcr}$
(4.2)から
S=rs
を分子の１つのSに代入すると
$\sin A+ \sin B+ \sin C=\frac{4Srs}{abcr}=\frac{4sS}{abc}$
よって等式(4.7)が成り立つ

(4.8)←
（左辺） $=(b^2+ c^2-a^2)\frac{\sin A}{\cos A}$
$=(b^2+ c^2-a^2)\frac{\frac{a}{2R}}{\frac{b^2+ c^2-a^2}{2bc}}$
$=(b^2+ c^2-a^2)\times\frac{a}{2R}\times\frac{2bc}{b^2+ c^2-a^2}$
$=\frac{abc}{R}$
(4.4)から
$\frac{abc}{R}=4S$
だから
（左辺）=S=（右辺）
よって等式(4.8)が成り立つ

(4.9)←
右図において，x, y, zで示した部分の長さはそれぞれ等しく
2x+2y+2z=a+b+c
$x+ y+ z=\frac{a+ b+ c}{2}=s$
またa=y+zだから
x=s−a
右図において，頂点Aから内接円の中心に引いた線は∠Aの二等分線だから
$\tan\frac{A}{2}=\frac{r}{x}=\frac{r}{s-a}$
よって等式(4.9)が成り立つ

(4.10)←
三角形の３辺の長さは正だから，(相加平均)≧(相乗平均)の関係が成り立つ．
$\frac{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}}{3}\underline{\ge}\sqrt[3]{\frac{1}{abc}}\hspace{5}(\gt 0)$
$\frac{a+ b+ c}{3}\underline{\ge}\sqrt[3]{abc}\hspace{5}(\gt 0)$
両辺とも正だから，辺々掛けると
$\frac{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}}{3}\times\frac{a+ b+ c}{3}\underline{\ge}1$
$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\underline{\ge}\frac{9}{a+ b+ c}$
ここでa+b+c=2sだから
$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\underline{\ge}\frac{9}{2s}$
よって不等式(4.10)が成り立つ

(4.11)←
ヘロンの公式から
$S=\sqrt{s(s-a)(s-b)(s-c)}$
$S^2=s(s-a)(s-b)(s-c)$ …(*)
ここで，三角形の２辺の和は他の１辺よりも大きいから
b+c−a>0, c+a−b>0, a+b−c>0
$s-a=\frac{b+ c-a}{2}\gt 0$
$s-b=\frac{c+ a-b}{2}\gt 0$
$s-c=\frac{a+ b-c}{2}\gt 0$
そこで，正の数s−a, s−b, s−cに(相加平均)≧(相乗平均)の関係を適用すると
$(s-a)(s-b)(s-c)\underline{\le}\{\frac{(s-a)+ (s-b)+ (s-c)}{3}\}^3$
$=\{\frac{3s-(a+ b+ c)}{3}\}^3=(\frac{3s-2s}{3})^3=(\frac{s}{3})^3=\frac{s^3}{27}$
(*)から
$S^2\underline{\le}s\times\frac{s^3}{27}$
$S^2\underline{\le}\frac{s^4}{27}$
$s^2\underline{\ge}3\sqrt{3}S$
よって不等式(4.11)が成り立つ

数学Ⅱの加法定理，倍角，半角公式に関するもの

■「次の等式を証明せよ」という問題の場合■
$\sin A+\sin B+\sin C=4\cos\frac{A}{2}\cos\frac{B}{2}\cos\frac{C}{2}$ …(5.1)
$\sin 2A+\sin 2B+\sin 2C=4\sin A\sin B\sin C$ …(5.2)

$\cos A+\cos B+\cos C=4\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2}+ 1$ …(5.3)
$\cos 2A+\cos 2B+\cos 2C=-4\cos A\cos B\cos C-1$ …(5.4)

$\tan A+\tan B+\tan C=\tan A\tan B\tan C$ …(5.5)
$\tan 2A+\tan 2B+\tan 2C=\tan 2A\tan 2B\tan 2C$ …(5.6)
$\tan\frac{A}{2}\tan\frac{B}{2}+\tan\frac{B}{2}\tan\frac{C}{2}+\tan\frac{C}{2}\tan\frac{A}{2}=1$ …(5.7)
$\cot\frac{A}{2}+\cot\frac{B}{2}+\cot\frac{C}{2}=\cot\frac{A}{2}\cot\frac{B}{2}\cot\frac{C}{2}$ …(5.8)

(5.1)←

$\sin A+\sin B+\sin C=2\sin\frac{A+ B}{2}\cos\frac{A-B}{2}+ \sin C$
$=2\sin (\frac{\pi-C}{2})\cos\frac{A-B}{2}+ \sin C$
$=2\sin (\frac{\pi}{2}-\frac{C}{2})\cos\frac{A-B}{2}+ 2\sin\frac{C}{2}\cos\frac{C}{2}$
$=2\cos\frac{C}{2}\cos\frac{A-B}{2}+ 2\sin\frac{C}{2}\cos\frac{C}{2}$
$=2\cos\frac{C}{2}(\cos\frac{A-B}{2}+ \sin\frac{C}{2})$
$=2\cos\frac{C}{2}(\cos\frac{A-B}{2}+ \sin\frac{\pi-A-B}{2})$
$=2\cos\frac{C}{2}\{\cos\frac{A-B}{2}+ \sin(\frac{\pi}{2}-\frac{A+ B}{2})\}$
$=2\cos\frac{C}{2}(\cos\frac{A-B}{2}+ \cos\frac{A+ B}{2})$
$=2\cos\frac{C}{2}(\cos\frac{A}{2}\cos\frac{B}{2}+\sin\frac{A}{2}\sin\frac{B}{2}$
$+\cos\frac{A}{2}\cos\frac{B}{2}-\sin\frac{A}{2}\sin\frac{B}{2})$
$=4\cos\frac{A}{2}\cos\frac{B}{2}\cos\frac{C}{2}$
よって等式(5.1)が成り立つ

(5.2)←

$\sin 2A+\sin 2B+\sin 2C$
$=2\sin(A+ B)\cos(A-B)+\sin 2C$
$=2\sin(\pi-C)\cos(A-B)+ 2\sin C\cos C$
$=2\sin C\cos(A-B)+ 2\sin C\cos C$
$=2\sin C\{\cos(A-B)+\cos C\}$
$=2\sin C\{\cos(A-B)+\cos (\pi-A-B)\}$
$=2\sin C\{\cos(A-B)-\cos (A+ B)\}$
$=4\sin C\sin A\sin B$
よって等式(5.2)が成り立つ

(5.3)←

$\cos A+\cos B+\cos C$
$=2\cos\frac{A+ B}{2}\cos\frac{A-B}{2}+\cos C$
$=2\cos\frac{\pi-C}{2}\cos\frac{A-B}{2}+ 1-2\sin^2\frac{C}{2}$
$=2\sin\frac{C}{2}\cos\frac{A-B}{2}+ 1-2\sin^2\frac{C}{2}$
$=2\sin\frac{C}{2}(\cos\frac{A-B}{2}-\sin\frac{C}{2})+ 1$
$=2\sin\frac{C}{2}(\cos\frac{A-B}{2}-\sin\frac{\pi-A-B}{2})+ 1$
$=2\sin\frac{C}{2}(\cos\frac{A-B}{2}-\cos\frac{A+ B}{2})+ 1$
$=2\sin\frac{C}{2}(-2\sin\frac{A}{2}\sin\frac{-B}{2})+ 1$
$=4\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2}+ 1$
よって等式(5.3)が成り立つ

(5.4)←

$\cos 2A+\cos 2B+\cos 2C$
$=2\cos(A+ B)\cos(A-B)+\cos 2C$
$=2\cos(\pi-C)\cos(A-B)+\cos 2C$
$=-2\cos C\cos(A-B)+ 2\cos^2C-1$
$=2\cos C\{\cos C-\cos(A-B)\}-1$
$=2\cos C\{\cos(\pi-A-B)-\cos(A-B)\}-1$
$=2\cos C\{-\cos(A+ B)-\cos(A-B)\}-1$
$=-2\cos C\{\cos(A+ B)+\cos(A-B)\}-1$
$=-2\cos C(2\cos A\cos B)-1$
$=-4\cos A\cos B\cos C-1$
よって等式(5.4)が成り立つ

(5.5)←

$\tan A=\tan (\pi-B-C)=-\tan(B+ C)$ $=-\frac{\tan B+\tan C}{1-\tan B\tan C}$
分母を払うと
$\tan A(1-\tan B\tan C)=-\tan B-\tan C$
$\tan A+\tan B+\tan C=\tan A\tan B\tan C$
よって等式(5.5)が成り立つ

(5.6)←

$\tan 2A=\tan (2\pi-2B-2C)=-\tan(2B+ 2C)$ $=-\frac{\tan 2B+\tan 2C}{1-\tan 2B\tan 2C}$
分母を払うと
$\tan 2A(1-\tan 2B\tan 2C)=-\tan 2B-\tan 2C$
$\tan 2A+\tan 2B+\tan 2C=\tan 2A\tan 2B\tan 2C$
よって等式(5.6)が成り立つ

(5.7)←

$\tan(\frac{A}{2}+\frac{B}{2})=\frac{\tan\frac{A}{2}+\tan\frac{B}{2}}{1-\tan\frac{A}{2}\tan\frac{B}{2}}$
$\tan(\frac{A}{2}+\frac{B}{2})=\tan(\frac{\pi}{2}-\frac{C}{2})=\frac{1}{\tan\frac{C}{2}}$
したがって
$\frac{\tan\frac{A}{2}+\tan\frac{B}{2}}{1-\tan\frac{A}{2}\tan\frac{B}{2}}=\frac{1}{\tan\frac{C}{2}}$
分母を払うと
$\tan\frac{A}{2}\tan\frac{C}{2}+\tan\frac{B}{2}\tan\frac{C}{2}=1-\tan\frac{A}{2}\tan\frac{B}{2}$
$\tan\frac{A}{2}\tan\frac{B}{2}+\tan\frac{B}{2}\tan\frac{C}{2}+\tan\frac{C}{2}\tan\frac{A}{2}=1$
よって等式(5.7)が成り立つ

(5.8)←
(5.7)の両辺を $\tan\frac{A}{2}\tan\frac{B}{2}\tan\frac{C}{2}$ で割ると得られる

形状問題

数学Ⅰの正弦定理で解けるもの

■「次の等式が成り立つとき，この三角形ABCはどのような形の三角形か」という問題の場合■

$a\sin A=b\sin B+ c\sin C$ …(6.1)
$\sin^2A=\sin^2B+ \sin^2C$ …(6.2)
$a\sin A=(b+ c)(\sin B-\sin C)$ …(6.3)
$(\sin A+\sin B+\sin C)(\sin B+\sin C-\sin A)$
$=3\sin B\sin C$ …(6.4)
$(b-c)\cos^2A=b\cos^2B-c\cos^2C$ …(6.5)

三角形の形状問題も，角度に関する式を辺に関する式に直してから考えるのが基本です．
a=bなどa=bの→二等辺三角形
a2=b2+c2など→∠A=90°の直角三角形
などど答えます．
（単に「二等辺三角形」と答えると，どの２辺が等しいのか分かりませんので，等しい２辺も書くようにします．）
a2=b2+c2などは，辺に関する式から角に関する結論を出すものですが，これは中学校で習う三平方の定理の逆なので，簡単に分かるでしょう．
　詳しく言えば， $\cos A=\frac{b^2+ c^2-a^2}{2bc}=0$ からA=90°ということですが，このように基本に立ち帰って考える練習をしておくと，次のような応用的な問題でも対応できるようになります．
a2=b2+c2+bcならば
$\cos A=\frac{b^2+ c^2-a^2}{2bc}=\frac{-bc}{2bc}=-\frac{1}{2}\rightarrow A=120^{\circ}$
などと答えることができます．

※以下において，式(m.n)→という記号は，式(m.n)を変形するという意味です

（解説）
(6.1)→
$a\sin A=b\sin B+ c\sin C$ に $\sin A=\frac{a}{2R}$ などを代入すると
$a\times\frac{a}{2R}=b\times\frac{b}{2R}+ c\times\frac{c}{2R}$
$a^2=b^2+ c^2$
∠A=90°の直角三角形…(答)

(6.2)→
$\sin^2A=\sin^2B+ \sin^2C$ に $\sin A=\frac{a}{2R}$ などを代入すると
$(\frac{a}{2R})^2=(\frac{b}{2R})^2+ (\frac{c}{2R})^2$
$a^2=b^2+ c^2$
∠A=90°の直角三角形…(答)

(6.3)→
$a\sin A=(b+ c)(\sin B-\sin C)$ に $\sin A=\frac{a}{2R}$ などを代入すると
$a\times\frac{a}{2R}=(b+ c)(\frac{b}{2R}-\frac{c}{2R})$
$a^2=b^2-c^2$
$a^2+ c^2=b^2$
∠B=90°の直角三角形…(答)

(6.4)→
$(\sin A+\sin B+\sin C)(\sin B+\sin C-\sin A)$
$=3\sin B\sin C$
に $\sin A=\frac{a}{2R}$ などを代入すると
$(\frac{a}{2R}+\frac{b}{2R}+\frac{c}{2R})(\frac{b}{2R}+\frac{c}{2R}-\frac{a}{2R})=3\frac{b}{2R}\cdot\frac{c}{2R}$
$\{(b+ c)+ a\}\{(b+ c)-a\}=3bc$
$(b+ c)^2-a^2=3bc$
$b^2+ 2bc+ c^2-a^2=3bc$
$b^2+ c^2-a^2=bc$
$\cos A=\frac{b^2+ c^2-a^2}{2bc}=\frac{bc}{2bc}=\frac{1}{2}$
∠A=60°の三角形…(答)

(6.5)→

※一般には， $\cos A=\frac{b^2+ c^2-a^2}{2bc}$ などを使って，角を辺に直すのが基本ですが，この問題のように $\cos^2A$ がある場合には，その式が複雑になりすぎます．
次のように， $\cos^2A=1-\sin^2A$ を使うともっと簡単にできます．

$(b-c)(1-\sin^2A)=b(1-\sin^2B)-c(1-\sin^2C)$
$(b-c)(1-\frac{a^2}{4R^2})=b(1-\frac{b^2}{4R^2})-c(1-\frac{c^2}{4R^2})$
$b-c-\frac{a^2(b-c)}{4R^2}=b-\frac{b^3}{4R^2}-c+\frac{c^3}{4R^2}$
$\frac{a^2(c-b)}{4R^2}=\frac{c^3}{4R^2}-\frac{b^3}{4R^2}$
$a^2(c-b)=c^3-b^3$
$a^2(c-b)=(c-b)(c^2+ bc+ b^2)$
$(c-b)(c^2+ bc+ b^2-a^2)=0$
$c-b=0$ …(*)または $c^2+ b^2-a^2=-bc$ …(**)
(*)よりb=cの二等辺三角形
(**)より $\cos A=\frac{b^2+ c^2-a^2}{2bc}=\frac{-bc}{2bc}=-\frac{1}{2}$
∠A=120°の三角形
ゆえに，b=cの二等辺三角形または∠A=120°の三角形…(答)

数学Ⅰの余弦定理で解けるもの

■「次の等式が成り立つとき，この三角形ABCはどのような形の三角形か」という問題の場合■

$c=2a\cos B$ …(7.1)
$a\cos B=b\cos A$ …(7.2)
$ca\cos A-bc\cos B=(a^2-b^2)\cos C$ …(7.3)
$b\cos C-c\cos B=a$ …(7.4)
$a\cos A+ b\cos B=c\cos C$ …(7.5)
$\frac{a}{\cos A}=\frac{b}{\cos B}=\frac{c}{\cos C}$ …(7.6)

（解説）
(7.1)→
$c=2a\cos B$ に $\cos B=\frac{c^2+ a^2-b^2}{2ca}$ を代入すると
$c=2a\times\frac{c^2+ a^2-b^2}{2ca}$
$c^2=c^2+ a^2-b^2$
$a^2=b^2$
$a,\hspace{5}b\gt 0$ だから
a=bの二等辺三角形…(答)

(7.2)→
$a\cos B=b\cos A$ に $\cos B=\frac{c^2+ a^2-b^2}{2ca}$ などを代入すると
$a\times\frac{c^2+ a^2-b^2}{2ca}=b\times\frac{b^2+ c^2-a^2}{2bc}$
$c^2+ a^2-b^2=b^2+ c^2-a^2$
$a^2=b^2$
a, b>0だから
a=bの二等辺三角形…(答)

(7.3)→
$ca\cos A-bc\cos B=(a^2-b^2)\cos C$ に

$\cos A=\frac{b^2+ c^2-a^2}{2bc}$ などを代入すると
$ca\times\frac{b^2+ c^2-a^2}{2bc}-bc\times\frac{c^2+ a^2-b^2}{2ca}=(a^2-b^2)\frac{a^2+ b^2-c^2}{2ab}$

$\cos A=\frac{b^2+ c^2-a^2}{2bc}$ などを代入すると
$ca\times\frac{b^2+ c^2-a^2}{2bc}-bc\times\frac{c^2+ a^2-b^2}{2ca}=(a^2-b^2)\frac{a^2+ b^2-c^2}{2ab}$
$a\times\frac{b^2+ c^2-a^2}{2b}-b\times\frac{c^2+ a^2-b^2}{2a}=(a^2-b^2)\frac{a^2+ b^2-c^2}{2ab}$
$a^2(b^2+ c^2-a^2)-b^2(c^2+ a^2-b^2)=(a^2-b^2)(a^2+ b^2-c^2)$
$a^2b^2+ a^2c^2-a^4-b^2c^2-b^2a^2+ b^4$
$=a^4+ a^2b^2-a^2c^2-a^2b^2-b^4+ b^2c^2$
$2a^4-2a^2c^2-2b^4+ 2b^2c^2=0$
$a^4-a^2c^2-b^4+ b^2c^2=0$
$a^4-b^4-c^2(a^2-b^2)=0$
$(a^2-b^2)(a^2+ b^2-c^2)=0$
ゆえに，a=bの二等辺三角形または∠C=90°の直角三角形…(答)

(7.4)→
$b\cos C-c\cos B=a$ に

$\cos C=\frac{a^2+ b^2-c^2}{2ab}$ などを代入すると
$b\times\frac{a^2+ b^2-c^2}{2ab}-c\times\frac{c^2+ a^2-b^2}{2ca}=a$
$\frac{a^2+ b^2-c^2}{2a}-\frac{c^2+ a^2-b^2}{2a}=a$
$(a^2+ b^2-c^2)-(c^2+ a^2-b^2)=2a^2$
$2b^2=2a^2+ 2c^2$
$b^2=a^2+ c^2$
ゆえに，∠B=90°の直角三角形…(答)

(7.5)→
$a\cos A+ b\cos B=c\cos C$ に

$\cos A=\frac{b^2+ c^2-a^2}{2bc}$ などを代入すると
$a\times\frac{b^2+ c^2-a^2}{2bc}+ b\times\frac{c^2+ a^2-b^2}{2ca}=c\times\frac{a^2+ b^2-c^2}{2ab}$
$a^2(b^2+ c^2-a^2)+ b^2(c^2+ a^2-b^2)=c^2(a^2+ b^2-c^2)$
$a^2b^2+ a^2c^2-a^4+ b^2c^2+ a^2b^2-b^4=c^2a^2+ b^2c^2-c^4$
$c^4=(a^2-b^2)^2$
$(c^2+ a^2-b^2)(c^2-a^2+ b^2)=0$
ゆえに，∠A=90°の直角三角形または∠B=90°の直角三角形…(答)

(7.6)→
$\frac{a}{\cos A}=\frac{b}{\cos B}=\frac{c}{\cos C}$ に

$\cos A=\frac{b^2+ c^2-a^2}{2bc}$ などを代入すると
$\frac{a}{\frac{b^2+ c^2-a^2}{2bc}}=\frac{b}{\frac{c^2+ a^2-b^2}{2ca}}=\frac{c}{\frac{a^2+ b^2-c^2}{2ab}}$

$\frac{2abc}{b^2+ c^2-a^2}=\frac{2abc}{c^2+ a^2-b^2}=\frac{2abc}{a^2+ b^2-c^2}$

$b^2+ c^2-a^2=c^2+ a^2-b^2=a^2+ b^2-c^2$

$b^2+ c^2-a^2=c^2+ a^2-b^2$
$c^2+ a^2-b^2=a^2+ b^2-c^2$ (連立！)
$b^2+ c^2-a^2=c^2+ a^2-b^2$ よりa=b
$c^2+ a^2-b^2=a^2+ b^2-c^2$ よりb=c
ゆえに，a=b=cとなって正三角形…(答)

数学Ⅰの正弦定理・余弦定理で解けるもの

■「次の等式が成り立つとき，この三角形ABCはどのような形の三角形か」という問題の場合■

$2\cos B\sin C=\sin A$ …(8.1)
$\sin A\cos B=\sin B\cos A$ …(8.2)
$\sin C+\sin B=\sin A(\cos C+\cos B)$ …(8.3)
$\sin A\cos A+\sin B\cos B=\sin C\cos C$ …(8.4)
$\tan A:\tan B=a^2\hspace{3}:\hspace{3}b^2$ …(8.5)
$\tan A\sin^2B=\tan B\sin^2A$ …(8.6)
$b^2\sin^2C+ c^2\sin^2B=2bc\cos B\cos C$ …(8.7)

（解説）
(8.1)→
$2\cos B\sin C=\sin A$ に

$\sin A=\frac{a}{2R},\hspace{5}\cos B=\frac{c^2+ a^2-b^2}{2ca}$ などを代入すると
$2\times\frac{c^2+ a^2-b^2}{2ca}\times\frac{c}{2R}=\frac{a}{2R}$
$c^2+ a^2-b^2=a^2$
$c^2=b^2$
ゆえに，b=cの二等辺三角形…(答)

(8.2)→
$\sin A\cos B=\sin B\cos A$ に

$\sin A=\frac{a}{2R},\hspace{5}\cos B=\frac{c^2+ a^2-b^2}{2ca}$ などを代入すると
$\frac{a}{2R}\times\frac{c^2+ a^2-b^2}{2ca}=\frac{b}{2R}\times\frac{b^2+ c^2-a^2}{2bc}$
$c^2+ a^2-b^2=b^2+ c^2-a^2$
$2a^2=2b^2$
$a^2=b^2$
ゆえに，a=bの二等辺三角形…(答)
※この問題については，原式から $A\ne 90^{\circ},\hspace{5}B\ne 90^{\circ}$ のとき
$\tan A=\tan B$ からA=Bを導く短縮答案が可能であるが，例外処理が長くなる
（A=90°のときは，原式から $\cos B=0\rightarrow B=90^{\circ}$ となって矛盾.B=90°のときも同様に矛盾．以上からA, B≠90°を言う）

(8.3)→
$\sin C+\sin B=\sin A(\cos C+\cos B)$ に

$\sin C=\frac{c}{2R},\hspace{5}\cos C=\frac{a^2+ b^2-c^2}{2ab}$ などを代入すると
$\frac{c}{2R}+\frac{b}{2R}=\frac{a}{2R}(\frac{a^2+ b^2-c^2}{2ab}+\frac{c^2+ a^2-b^2}{2ca})$
$c+ b=\frac{a^2+ b^2-c^2}{2b}+\frac{c^2+ a^2-b^2}{2c}$
$2bc(c+ b)=c(a^2+ b^2-c^2)+ b(c^2+ a^2-b^2)$
$2b^2c+ 2bc^2=a^2c+ b^2c-c^3+ bc^2+ a^b-b^3$
$(b^3+ b^2c+ bc^2+ c^3)-(a^2c+ a^2b)=0$
$b^2(b+ c)+ c^2(b+ c)-a^2(b+ c)=0$
$(b+ c)(b^2+ c^2-a^2)=0$
b+c>0により，∠A=90°の直角三角形…(答)

(8.4)→
$\sin A\cos A+\sin B\cos B=\sin C\cos C$ に

$\sin A=\frac{a}{2R},\hspace{5}\cos A=\frac{b^2+ c^2-a^2}{2bc}$ などを代入すると
$\frac{a}{2R}\times\frac{b^2+ c^2-a^2}{2bc}+\frac{b}{2R}\times\frac{c^2+ a^2-b^2}{2ca}=\frac{c}{2R}\times\frac{a^2+ b^2-c^2}{2ab}$

$\frac{a(b^2+ c^2-a^2)}{bc}+\frac{b(c^2+ a^2-b^2)}{ca}=\frac{c(a^2+ b^2-c^2)}{ab}$

$a^2(b^2+ c^2-a^2)+ b^2(c^2+ a^2-b^2)=c^2(a^2+ b^2-c^2)$

$a^2b^2+ a^2c^2-a^4+ b^2c^2+ a^2b^2-b^4=c^2a^2+ b^2c^2-c^4$

$a^4+ b^4-2a^2b^2-c^4=0$

$(a^2-b^2)^2-c^4=0$

$(a^2-b^2+ c^2)(a^2-b^2-c^2)=0$

$a^2+ c^2=b^2$ または $a^2=b^2+ c^2$
ゆえに，∠A=90°の直角三角形または∠B=90°の直角三角形…(答)

(8.5)→
$\tan A:\tan B=a^2\hspace{3}:\hspace{3}b^2$
$\frac{\sin A}{\cos A}\hspace{5}:\hspace{5}\frac{\sin B}{\cos B}=a^2\hspace{3}:\hspace{3}b^2$

に $\sin A=\frac{a}{2R},\hspace{5}\cos A=\frac{b^2+ c^2-a^2}{2bc}$ などを代入すると
$\frac{\frac{a}{2R}}{\frac{b^2+ c^2-a^2}{2bc}}\hspace{5}:\hspace{5}\frac{\frac{b}{2R}}{\frac{c^2+ a^2-b^2}{2ca}}=a^2\hspace{3}:\hspace{3}b^2$
$\frac{\strike{a}}{\strike{2R}}\times\frac{\strike{2bc}}{b^2+ c^2-a^2}\times b^2=\frac{\strike{b}}{\strike{2R}}\times\frac{\strike{2ca}}{c^2+ a^2-b^2}\times a^2$
$b^2(c^2+ a^2-b^2)=a^2(b^2+ c^2-a^2)$
$b^2c^2+ a^2b^2-b^4=a^2b^2+ a^2c^2-a^4$
$a^4-b^4-a^2c^2+ b^2c^2=0$
$(a^2-b^2)(a^2+ b^2)-c^2(a^2-b^2)=0$
$(a^2-b^2)(a^2+ b^2-c^2)=0$
ゆえに，a=bの二等辺三角形または∠C=90°の直角三角形…(答)

(8.6)→
$\tan A\sin^2B=\tan B\sin^2A$
$\frac{\sin A}{\cos A}\sin^2B=\frac{\sin B}{\cos B}\sin^2A$
$\sin A,\hspace{5}\sin B\gt 0$ により，両辺を $\sin A\cdot\sin B\gt 0$ で割ると
$\frac{\sin B}{\cos A}=\frac{\sin A}{\cos B}$
$\sin B\cos B=\sin A\cos A$

この式に $\sin A=\frac{a}{2R},\hspace{5}\cos A=\frac{b^2+ c^2-a^2}{2bc}$ などを代入すると
$\frac{b}{2R}\times\frac{c^2+ a^2-b^2}{2ca}=\frac{a}{2R}\times\frac{b^2+ c^2-a^2}{2bc}$

$\frac{b(c^2+ a^2-b^2)}{a}=\frac{a(b^2+ c^2-a^2)}{b}$

$b^2(c^2+ a^2-b^2)=a^2(b^2+ c^2-a^2)$

$b^2c^2+ a^2b^2-b^4=a^2b^2+ a^2c^2-a^4$

$a^4-b^4+ b^2c^2-a^2c^2=0$

$(a^2-b^2)(a^2+ b^2)+ c^2(b^2-a^2)=0$

$(a^2-b^2)(a^2+ b^2-c^2)=0$
ゆえに，a=bの二等辺三角形または∠C=90°の直角三角形…(答)

(8.7)→

※普通に変形すると，左辺に2Rが残ってしまうので，これを避けるために一時的に $\sin^2C$ などを $1-\cos^2C$ で表してみる

$b^2(1-\cos^2C)+ c^2(1-\cos^2B)=2bc\cos B\cos C$
$b^2+ c^2=b^2\cos^2C+ 2bc\cos B\cos C+ c^2\cos^2 B$
$b^2+ c^2=(b\cos C+ c\cos B)^2$
ここで，第1余弦定理により $b\cos C+ c\cos B=a$ だから
$b^2+ c^2=a^2$
ゆえに，∠A=90°の直角三角形…(答)

...（携帯版）メニューに戻る

...メニューに戻る