.

■　回帰直線，回帰係数

［目次］
･･･簡単な内容
　回帰直線とは
　Excelの散布図に回帰式を追加する方法（これが簡単）
　Excelのワークシート関数を使って回帰式を計算する方法
　Excelの分析ツールを使って回帰式を求める方法
　目的変数の予測値を数値として求める方法

･･･やや難しい内容
　最小二乗法の原理にさかのぼってExcelのソルバーを用いて回帰式を求める方法
　最小二乗法によって回帰直線を求める考え方 		表１
観測値 変数ｘ 変数ｙ
No.1 1.8 2.0
No.2 2.3 3.7
No.3 4.1 2.7
No.4 6.5 4.5
No.5 5.2 4.6


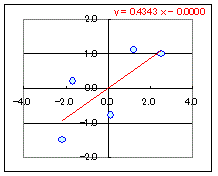
図１
［記号・用語］
◇独立変数・説明変数・予測変数
　　･･･変数ｘの値から変数ｙの値を予測するとき，変数ｘを独立変数（数学ではこの用語がよく用いられる）・説明変数・予測変数（統計ではこの用語がよく用いられる）などという．

◇従属変数・目的変数
　　･･･変数ｘの値から変数ｙの値を予測するとき，変数ｙを従属変数（数学ではこの用語がよく用いられる）・目的変数（統計ではこの用語がよく用いられる）などという．

◇観測値，予測値，平均値
　　･･･観測値を表す変数は x , y ， 個々の観測値は xi , yi ，予測値は ^y （ワイ・ハットやワイ・カレットなどと読む），平均値は -x，-y と書く．予測値は変数であるが平均値は定数		 ［英語］
回帰直線　regression line
回帰係数 regression coefficient
偏回帰係数 partial regression coefficient
回帰分析 regression analysis
重回帰分析 multiple regression analysis
観測値 変数ｘ 変数ｙ 予測値^y
No.1 1.8 2.0 2.6
No.2 2.3 3.7 2.8
No.3 4.1 2.7 3.6
No.4 6.5 4.5 4.6
No.5 5.2 4.6 4.0
　 　 　 　
平均値 4.0 3.5 　


［本文］
○　回帰直線とは
　右上の表１のような観測データにおいて変数ｘの値から変数ｙの値を予測する式を１次式で求めたものを回帰式という．
　表１を散布図に表したものが図１とすると，回帰式は図１において赤で示した直線の方程式となっている．
　回帰式を y=α+βx　とするとき,αを定数項，βを回帰係数（単回帰係数）という．
　（表1，図１の回帰式はy=0.4343x+1.7716 になる．）

　回帰式はｘの値が与えられたときにｙの値を予測するもので，右図１において赤で示した直線が元の観測データの点を正確には通っていない（３つ以上の点を１つの直線で結ぶことは，一般にはできない．）ことからわかるように，予測式であり近似式となっている．
　回帰直線は，ｘの値に対するｙの予測値と実際のｙの観測値との誤差(*1)が最も小さくなる直線である．

　表１のように１つの変数の値によって他の変数の値を予測するものを単回帰分析といい､２つ以上の変数から他の変数の値を予測するものを重回帰分析という．

図2
(*1)　図2の誤差（観測値ｙ1と予測値との差：残差と呼ばれる）の２乗和が最小となるような直線を選ぶ．

○　Excelの散布図に回帰式を追加する方法
･･･単回帰分析ではこの方法が簡単（説明変数が２つ以上あるときは散布図が描けないから，この方法は使えない．）

次の手順でグラフ上に回帰式が表示される．
散布図の作成→近似曲線の表示→近似曲線のオプション指定
　上の表１を使うには，表全体をドラッグ・コピーしてからExcel上に貼り付けるとよい．
　このまま使えばｘが説明変数，ｙが目的変数となるが，各自で作成したデータで右側の列に説明変数が並んでいるときは，得られるものが違うので注意を要する．一般に，ｘからｙを予測する式を裏返してもｙからｘを予測する式にはならない．
◇Excel2007の場合◇
(1)散布図を表示するには
　Excel上で，表1の色付けした部分（No.を含まない部分）を選択して，挿入→散布図→左上の線なしパターンを選ぶ
(2)近似曲線を追加するには
　散布図上の１つの点を右クリックし，近似曲線の追加を選ぶ→上から２つ目の線形近似→閉じる
(3)回帰式を表示するには
　(2)で表示された直線上をポイントして右クリックし，近似曲線の書式設定を選ぶ→「グラフに数式を表示する」だけにチェックを付け切片にはチェックを付けない(*1)→閉じる
　回帰式の文字サイズ，文字色，表示位置などはその式をクリックすると変更できる．
 ◇Excel2002の場合◇
(1)散布図を表示するには
　Excel上で，表1の色付けした部分（No.を含まない部分）を選択して，挿入→グラフ→散布図→左上の線なしパターンを選ぶ→次へ→（データ範囲にタイトル行も入っており，系列が列になっていれば）次へ→次へ→完了

(2)近似曲線を追加するには
　散布図上の１つの点を右クリックし，近似曲線の追加を選ぶ→左上端の線形近似→OK

(3)回帰式を表示するには
　(2)で表示された直線上をポイントして右クリックし，近似曲線の書式設定を選ぶ→オプションのタブを選ぶ→「グラフに数式を表示する」だけにチェックを付け切片にはチェックを付けない(*2)→OK
(*2)「観測データ」を加工した「中心化データ」や「標準化データ」を扱っているときは回帰式の定数項（切片）が０になるはず(*3)だから，「切片」という項目にもチェックを入れて定数項が０になるようにする．
中心化データ 変数ｘ 変数ｙ 変数ｘ'=xi-x 変数ｙ'=yi-y
No.1 1.8 2 -2.2 -1.5
No.2 2.3 3.7 -1.7 0.2
No.3 4.1 2.7 0.1 -0.8
No.4 6.5 4.5 2.5 1.0
No.5 5.2 4.6 1.2 1.1
平均 3.98 3.5 0 0
　中心化データとは，観測値から各変数の平均値を引いた変数で表したもの．
　中心化データの回帰式は，観測値の回帰式と回帰係数βは変わらず，定数項α=0となる．(*3)回帰直線は各変数の平均値を座標とする点( x , y )を通る･･･証明は最小二乗法によって回帰直線を求める考え方の項･･･ので，観測値では各平均値，中心化データでは原点を通るはずになっている．
　さらに中心化データを各変数の標準偏差で割った標準化データで回帰式を求めているときは，回帰係数βは相関係数ｒに等しくなり，定数項αは0に等しくなる．･･･証明は最小二乗法によって回帰直線を求める考え方の項･･･

○　Excelのワークシート関数を使って回帰式を計算する方法
右の表2のようにデータがあるとき，式を書き込みたいセルをポイントしておく．
(1)数式を直接書き込むとき
線形回帰直線の切片を計算する関数 INTERCEPT() を用いて
定数項αを求めるには
=INTERCEPT(C2:C6,B2:B6)
のように書き込む．
*　右の表で色付けしたように，上端のラベルを含めない．
*　関数INTERCEPT()の引数として，第1引数に「既知のｙ」を与えることになっているので，黄色で示した目的変数の値のセル範囲を書き込み，第2引数に「既知のｘ」として水色で示した説明変数の値のセル範囲を書き込む．

回帰係数βを求めるには
=SLOPE(C2:C6,B2:B6)
のように書き込む．
*　αを求めたときと同様に第1引数が「既知のｙ」，第2引数が「既知のｘ」になっているので注意．
表2
　 A B C
1 観測値 変数ｘ 変数ｙ
2 No.1 1.8 2.0
2 No.2 2.3 3.7
4 No.3 4.1 2.7
5 No.4 6.5 4.5
6 No.5 5.2 4.6
7 　 　 　

(2)メニューに沿って関数を選択するとき
◇Excel2002，2007共通
ワークシートの上の方にある数式バーの左隣にfx という関数挿入アイコンがあるのでこれをクリックする．
［関数の分類］で統計を選択
［関数名］で各々INTRCEPT，SLOPEを選択して，左に述べたようにｙの範囲，ｘの範囲の順に指定する．
○　Excelの分析ツールを使って回帰式を求める方法
･･･この方法で求めるためには，
→Excelのオプション→アドインで「アクティブなアプリケーション　アドイン」に分析ツールが表示されなければならない．
　データ→（分析の中の）データ分析→回帰分析→OK
以後は右欄のExcel2002※と同様		 ◇Excel2002の場合◇
･･･この方法で求めるためには，「ツール」→「アドイン」で「分析ツール」にチェックがついていなければならない．
　ツール→分析ツール→回帰分析→ＯＫ
※
　入力ｙ範囲には表２の例では，変数ｙというラベルも含めて黄色で示した範囲を指定する．
　入力ｘ範囲には表２の例では変数ｘというラベルも含めて水色で示した範囲を指定する．
　入力元の「ラベル」という項目にチェックを入れる．
同一シート内に結果を出力するときは，出力オプションの項目で「一覧の出力先」を選び，出力したい範囲の左上端のセルを指定する
　３つのブロックに分かれて書き込まれる表のうち一番下の係数という項目が定数項α，回帰係数βを表す．
　 係数
切片 1.77
変数ｘ 0.43


○　目的変数の予測値を数値として求める方法
　上記のいずれかの方法によってαすなわちINTERCEPT，βすなわちSLOPEが得られているときは，その値を用いて既知のｘや未知のｘに対応するｙの予測値を計算することができる．
　右の表3においてNo.1〜No.5が既知のデータで，これらの値から変数ｘ=3.5のときの変数ｙの予測値を求めたいものとする．
　Excelのワークシート関数FORECASTを用いてC7のセルに予測値を書き込むには
=FORECAST(B7,C2:C6,B2:B6)
とする．
この関数は単回帰（１つの変数ｘから変数ｙの値を予測する）ときに使え，２つ以上の変数から予測する重回帰では利用できない．
次に述べる関数TREND()とは引数の順序が異なるので注意
Excelのワークシート関数TRENDを用いてC7のセルに予測値を書き込むには
=TREND(C2:C6,B2:B6, B7, 1)
とする．第4引数を省略するか１とかTRUEに指定すると定数項αを用いた予測式で計算され，第4引数を0とかFALSEに指定するとα=0とする予測式で計算される．		 表3
　　 A B C
1 観測値 変数ｘ 変数ｙ
2 No.1 1.8 2.0
2 No.2 2.3 3.7
4 No.3 4.1 2.7
5 No.4 6.5 4.5
6 No.5 5.2 4.6
7 　 3.5 　


※変数ｘ=3.5に対する変数ｙの予測値は3.29になる．

○　最小二乗法の原理にさかのぼってExcelのソルバーを用いて回帰式を求める方法
　右の表4において変数x､yの値B2:C6が固定されているときに，α，βの値B9:C9を変化させて，これらの値を用いて計算しているE2:E6の２乗和E8が最小となるようにα，βの値を求める．
(1)　セルB9,C9には適当な初期値0.5,0.5などを記入しておく．
(2)　D2に=$B$9+$C$9*B2という計算式を書き込み，これをD3:D6までコピー・貼り付けする．
　（これがそれぞれのα，βに対する予測値になっている）
(3)　E2に=C2-D2と書き込む．
　（これがそれぞれのα，βに対する残差の計算になっている）
(4)　E8に=SUMSQ(E2:E6)と書き込む．
　（これが残差２乗和の計算［B2^2+B3^2+･･･B6^2と同じ］になっている．）
◇Excel2007の場合
(5)　ツール→ソルバー
目的セルをE8に指定，目標値は最小値を選択
変化させるセルをB9:C9に指定
実行
最適解が見つかりました→解を記入する→OK
表4
　 A B C D E
1 観測値 変数ｘ 変数ｙ 予測値 残差
2 No.1 1.8 2.0 2.6 -0.6
3 No.2 2.3 3.7 2.8 0.9
4 No.3 4.1 2.7 3.6 -0.9
5 No.4 6.5 4.5 4.6 -0.1
6 No.5 5.2 4.6 4.0 0.6
7 　 　 　 　 　
8 　 α β ２乗和 2.2
9 　 1.772 0.434 　 　

◇Excel2002の場合
(5)　データ→（分析の中の）ソルバー
目的セルをE8に指定，目標値は最小値を選択
変化させるセルをB9:C9に指定
実行
最適解が見つかりました→解を記入する→OK

.
練習問題
［表を画面上でドラッグ・コピーしExcelに貼り付けるとよい］

　右の表は２つのテストの得点表である．
(1)　テスト１の得点からテスト２の得点を推定する回帰式を作れ．
(2)　テスト１が55点であるとき，テスト２の得点推定値を求めよ．
解答
(1)　y = 0.2188x + 40.985
(2)　53点
回答者 テスト1 テスト2
No.1 47 50
No.2 30 50
No.3 21 42
No.4 42 47
No.5 20 52
No.6 38 46
No.7 21 39
No.8 32 49
No.9 27 43
No.10 50 51
No.11 47 54
No.12 31 54
No.13 35 52
No.14 21 46
No.15 28 47
確率統計のメニューに戻る 高校数学のメニューに戻る
■［個別の頁からの質問に対する回答］[回帰直線，回帰係数について／16.11.24］
お世話になります。 データが「観測結果」の取り扱いとして大変わかりやすいと思うのですが、一つ質問があります。 データが「点群」の場合はいかがでしょうか？ 具体的には、一直線上にあるはずのものが千鳥足になっている場合、このページの手法でも「あるはずの直線」を求められるでしょうか？ （座標系が任意であっても同一の直線が得られるか？ということになります） 「回帰直線とは？」のあたりに補足として記載があれば最適と思います。
＝＞［作者］：連絡ありがとう．興味を持っていただいたということはありがたいことですが，質問内容をもっと絞ってください．
すなわち，質的に異なる内容が１つの質問として尋ねられていますので，整合的な回答を示すことができません．
(1) データが「点群」の場合は･･･通常の統計データは点群だと思いますので，この用語は何も限定しておらず，特に何も語っていません．
(2) 一直線上にあるはずのものが千鳥足になっている場合･･･通常の統計データは，千鳥足になっています．はじめから同一直線上にあれば，回帰直線は不要で数学で解けます．
(3) 座標系が任意であっても同一の直線が得られるか･･･「一般に，ｘからｙを予測する式を裏返してもｙからｘを予測する式にはならない．」と文章で示してあります．

　文章で回答すると以上のような味もそっけもないものになりますが，左図において図１の赤線はｘからｙを予測する直線で，図２の青線はｙからｘを予測する直線です．通常の場合これらは一致しません．