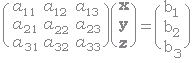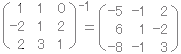○ 上の方程式を実際にExcelで求めて見よう
※ 定数 a11,a12,a13,・・・,a33,b1,b2,b3 が与えられているとき,x,y,z を未知数とする連立方程式
a11x + a12y +a13z = b1
a21x + a22y +a23z = b2
a31x + a32y +a33z = b3
は行列を用いて
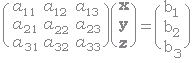 と書けるが,係数行列の逆行列が存在すればこれを両辺に左から掛けて
と書けるが,係数行列の逆行列が存在すればこれを両辺に左から掛けて
 が解となる.
が解となる.
※ はじめに,Excelの統計関数では説明変数が多変数になる場合に下図のように一連の範囲で指定する必要があるため,左端に目的変数,続いて説明変数1,説明変数2,・・・と必要に応じて列を追加して行けるようにしておくとよい.(Excel統計関数の引数は予測するyの範囲を先に書き,説明変数x1・・・の範囲を後に書くようになっている.実務上はその方が使いやすくなる.)
| 目的変数y |
説明変数x1 |
説明変数x2 |
・・・ |
説明変数xn |
| y1 |
x11 |
x21 |
・・・ |
xn1 |
| y2 |
x12 |
x22 |
・・・ |
xn2 |
| ・・・ |
・・・ |
・・・ |
・・・ |
・・・ |
| ym |
x1m |
x2m |
・・・ |
xnm |
これは連立方程式の右辺と左辺を入れ替えて,
b1 = a11x + a12y +a13z
b2 = a21x + a22y +a23z
b3 = a31x + a32y +a33z
の形で書いているのと同じことになる.
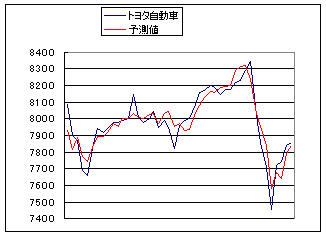
(1) 本題に戻って,次の表のように日付順にデータを作成しておく.
| |
トヨタ自動車
y |
円/usドル
x1 |
日経平均
x2 |
| 2007年1月4日 |
8,090 |
119.0199 |
17,354 |
| 2007年1月5日 |
7,900 |
118.5899 |
17,092 |
| 2007年1月9日 |
7,870 |
119.4 |
17,238 |
| 2007年1月10日 |
7,690 |
119.65 |
16,942 |
| 2007年1月11日 |
7,660 |
120.4499 |
16,838 |
| ・・・ |
・・・ |
・・・ |
・・・ |
(2)
Σy=an + bΣx1+cΣx2 ・・・(1)
Σyx1=aΣx1 + bΣx12+cΣx1x2 ・・・(2)
Σyx2=aΣx2 + bΣx1x2+cΣx22 ・・・(3)
の3つの方程式を(この段階では係数a,b,cが未知数)を作るためにあらかじめ,次の和を準備する.
| Σy |
n |
Σx1 |
Σx2 |
| Σyx1 |
Σx1 |
Σx1^2 |
Σx1x2 |
| Σyx2 |
Σx2 |
Σx1x2 |
Σx2^2 |
例えばΣyの欄には =SUM(B3:B47)などと書く.
nの欄には =COUNT(B3:B47)などと書く.次のような係数行列ができる.
| |
A |
B |
C |
D |
E |
| ・・・ |
・・・ |
・・・ |
・・・ |
・・・ |
・・・ |
| 54 |
|
359230 |
45 |
5396 |
784701 |
| 55 |
|
43084915 |
5396 |
647244 |
94111418 |
| 56 |
|
6266956012 |
784701 |
94111418 |
13689672141 |
(3) 右の解説のようにして逆行列を作る.
(4) 右の解説のように行列の積 A-1b を作る.
(5) 結果が次のように出る.
| -1205.071976 |
| 15.69689815 |
| 0.418952291 |
これより,a=-1205.07,b=15.6969,c=0.4190
したがって,y = -1205.07 + 15.6969x1 + 0.4190x2
が求まる. |
○ 行列の積の簡単な解説は[このページ]
○ 行列の積
 をExcelで求めるには
をExcelで求めるには
=MMULT(左から掛ける行列,右から掛ける行列) が使える.
| |
A |
B |
C |
D |
E |
F |
| 1 |
1 |
2 |
|
-2 |
|
0 |
| 2 |
3 |
4 |
|
1 |
|
-2 |
|
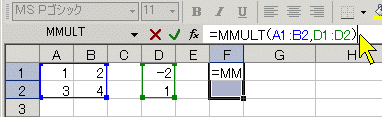
上のようにA1〜B2に2×2行列が入力されていて,これにD1からD2の2×1行列を掛けたものをF1からF2に出力したいとき
(1) まずF1のセルに次のように記入する.(直接書き込むまたはメニューから挿入→関数→数学/三角で選択する)
=MMULT(A1:B2,D1:D2)
これによりF1に1つの成分だけが書き込まれる.
(2) 答をExcelでいう配列の形(数学でいう行列の形)にするには,(1)の結果が書き込まれた後,積の結果の形2×1型に合わせてF1からF2までをドラッグで選択して(マウス形状十字のときに引っ張るのではない)反転表示にしてから,次のように「数式バー」と呼ばれる画面上のfxと書かれた欄にマウスをあてて,Ctrl キーと Shiftキーの両方を押しながらEnterキーを押す.
○ 逆行列の簡単な説明は[このページ]
○ 正方行列の逆行列をExcelで求めるには
=MINVERSE(元の行列の範囲) が使える.
逆行列を求める計算
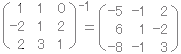 をExcelで行うには,
をExcelで行うには,
| |
A |
B |
C |
D |
E |
F |
G |
| 1 |
1 |
1 |
0 |
|
|
|
|
| 2 |
-2 |
1 |
2 |
|
|
|
|
| 3 |
2 |
3 |
1 |
|
|
|
|
上のようにA1〜C3に3×3行列の成分が入力されているとき,この行列の逆行列をE1からG3に出力するには
(1) E1に =MINVERSE(A1:C3) と記入する.(直接入力またはメニューから「挿入」→「関数」→「数学/三角」で選択し,入力範囲としてA1〜C3までを指定する.)
(2) 以上の操作で,セルE1に(1,1)成分が一つだけ書き込まれるので,次にこれを配列にして3×3の行列にする:
そのためには,(1)の結果が書き込まれた後,逆行列3×3型の形に合わせてE1からG3の範囲をドラッグにより反転表示させてから,行列の積のときと同様に,数式バーにマウスを当ててCtrl+Shift+Enterとする.
|