== 対応のある場合のｔ検定…例題・問題 ==
■対応のある場合のｔ検定を用いる例
　次にような場合に「対応のある場合のｔ検定」…「 一対の標本による平均の検定」「対応のある２群の平均値差の検定」「データに対応がある場合のｔ検定」とも呼ばれる…を用いる．
○１　同一の被験者に対して異なる２つの条件で測定したとき，それぞれの条件下での母集団平均が等しいかどうかの比較を行う場合
例１
　右の表１は定期健診での最高血圧の一覧表であるものとする．No欄は被験者の整理番号，Ａ欄は昨年の定期検査時の最高血圧，Ｂ欄は今年の定期検査時の最高血圧とする．
　この一覧表では12人の被験者について，昨年の定期検査時と今年の定期検査時の最高血圧が対のデータとなっている．
　これらのデータからＡ欄の値とＢ欄の値を比較すると，Ａ欄のデータとＢ欄のデータは同一被験者のデータであるので，昨年と今年という条件だけが異なることになり，昨年の最高血圧と今年の最高血圧に有意差があるかどうか調べることができる．（単にＡ欄とＢ欄のデータの件数が等しく，Ａ欄が昨年のＢ欄が今年のデータであるというだけで対応のあるｔ検定が使える訳ではなく，Ａ欄とＢ欄が同一被験者のデータとして対応があることが重要）
　この場合において，昨年と今年で有意差があるかどうかを調べるのだから両側検定を用いるとよい．
表１
Ｎｏ Ａ Ｂ
1 109 105
2 115 100
3 107 118
4 124 122
5 123 122
6 112 125
7 128 101
8 119 128
9 121 104
10 124 107
11 123 103
12 123 128

※例１のような検定を行うためには，母集団についてＡ欄のデータ，Ｂ欄のデータ，Ａ－Ｂの値が各々正規分布していることが前提となる．
　取り扱っているデータがそもそも正規分布にならないという有力な学説がある場合（例えば，演歌やロックのような特定ジャンルの音楽に対する大人の好感度，数学や英語などの教科に対する生徒の好き嫌いなどを数値化したとき，値は正規分布にならない･･･好き嫌いが分かれて双峰形になる･･･という有力な学説があれば），安易に正規分布を仮定できないが，特に引っかかる事情がなければ多くの場合，母集団の値の分布，差の分布は正規分布をなすものと見なせばよい．
※このような「対応のある場合のｔ検定」を適用する場合には，Ａ欄のデータとＢ欄のデータが等分散であるか否かによって，以後の処理を分ける必要はない．
例２
　右の表２はあるダイエット法を行う前と後の体重の一覧表であるものとする．No欄は被験者の整理番号，Ａ欄は実施前の体重，Ｂ欄は実施後の体重とする．
　この一覧表では8人の被験者について，ダイエット法実施前後の体重が対のデータとなっている．
　これらのデータからＡ欄の値とＢ欄の値を比較すると，Ａ欄のデータとＢ欄のデータは同一被験者のデータであるので，Ａ欄とＢ欄の差はダイエット法の効果と見ることができる．
　この場合，ダイエット法の効果があるとは「体重が減少している」という意味であるから片側検定を用いるとよい．
表２
No A前 B後
1 54.3 52.6
2 51.9 48.7
3 55.2 56.7
4 55.3 52.5
5 53.8 52.1
6 52.1 53.3
7 53.6 51.4
8 50.2 49.2

※片側検定の境界値は両側検定の境界値よりも内側に来るので，同じｔ値でも両側検定では棄却域に入らず片側検定ならば棄却域に入ることがある．
例３
　右の表３は２つの指導法Ａ，Ｂを行った後のある教科の得点一覧表であるものとする．No欄は被験者の整理番号，Ａは指導法Ａ，Ｂは指導法Ｂを行った後の得点とする．
　同一の被験者に相前後して異なる２つの指導法を行った場合には，後で行う指導のときに前に行った指導による影響が残っている場合がある．例えば，出題範囲が同一であるときの試験では，後で行う試験の得点が高くなると予想されるが，異なる出題範囲であっても前の指導によって「学習習慣が身についてくる」「学習意欲が変化してくる」といった間接的な影響は有り得る．
　このように，同一被験者に対して異なる２つの条件で試験を行うときに，順序による効果が有り得る場合は，被験者のうちの半数をＡ→Ｂの順に，残り半分をＢ→Ａの順に行うなどの工夫をしなければならない．（背景色がピンクのデータは先に行い，空色のデータは後で行うというように実施の順序を変える）
　順序の交換は表３の一覧表では数値としては表れておらず，後で解説するコンピュータ処理として行うことはできないので，この一覧表を作る前に行われている必要がある．
　このように,コンピュータ処理上は，ｔ検定が簡単に行えても，測定が２つの要因Ａ，Ｂの違いだけを反映しているかどうか，他の要因が入り込んでいないかということは，コンピュータ処理以前の測定の段階で考慮されていなければならない．そうでないと，ガラガラポン統計とかクリック統計などと悪口を言われても仕方がないような分析に陥ってしまう．
表３
Ｎｏ Ａ Ｂ
1 73 77
2 80 69
3 80 66
4 79 73
5 79 69
6 68 64
7 79 79
8 69 76
9 60 64
10 74 64
11 60 69
12 71 74
13 69 73
14 82 80
○２　被験者が異なっていても双子の兄弟姉妹，夫婦のように対応のある被験者のデータを比較する場合
例４
　右の表４は異なる環境で育った一卵性双生児の20歳の時点での体重の一覧表であるとする．Ｎｏは一卵性双生児の組の番号，Ａ，Ｂは各々の体重とする．
　一般に人間の特性や能力には遺伝的な要因（先天的なもの）と環境的な要因や本人の努力によって変わる要因（後天的なもの）があるので，遺伝的な要因が同じと見なせる組について，育った環境や教育・学習による差異があるかどうか調べることによって，身長・体重・能力・好みなどについて後天的な要因が大きいかどうかを調べることができる．
　後天的な要因が同じで，先天的な要因が異なる対を選ぶことによって先天的な要因の大きさを調べることも考えられる（両親が異なる子供を同一の家庭で育てている場合）．

　双子とか夫婦の対を選ぶのは，測定条件Ａ，Ｂ以外の要因を等質化してＡ，Ｂの違いによる差異を調べるためなので，これら以外に意識されていない要因が働く場合には単にｔ検定が結果が出たというだけでは何も示されていない場合がある．
　例えば，右の表が各々同居している夫婦のコレステロール値であるとき，夫婦は同じような食事をするので，食事が同じときにコレステロール値の高低に同じ傾向が見られるかどうか（同じメニューでもコレステロール値に差異があるかどうか）という調査で有り得る．しかし，Ａ欄を夫，Ｂ欄を妻に割り当てると，ＡＢ間には男女による差異が入ってしまうことになる．

※　このように，被験者が異なる場合でも「対応のある場合のｔ検定」を使うことがあるが，それらは測定条件Ａ，Ｂ以外の要因を等質化することがねらいである．
※　一般に，自然科学の実験とは異なり社会，心理，教育分野の測定では，非常に多くの要因が働いているので他の要因を完全に等しくすることはできない．そこで，他の要因が可能な限り等質になるようにサンプルの選び方を工夫するとともに，他の要因については相殺されるようにデータを配置する方がよい．（半数について測定の順序を入れ替える，夫と妻の欄を入れ替えるなど）
表４
Ｎｏ Ａ Ｂ
1 172 170
2 179 173
3 168 176
4 177 184
5 174 180
6 166 171
7 170 176
8 167 169
9 175 169
10 167 171
11 176 183
12 162 156
13 162 159
14 166 160
15 179 180
16 172 164
17 179 169
18 174 172
19 176 184
20 176 181
○３　中学１年生で，数学の担当者が異なる２つの学級から中学入学時の診断テストの得点が等しい対を選んで学年末の数学の得点を比較し，各担当者による教え方の違いによって学年末の得点に有意差があるかどうか比較する場合
※異なる２つの測定を同一環境で行う方が測定しようとしている要因以外の効果を等質化できるが，同時に２つを行えないことがある．（例えば生産者の氏名や似顔絵を貼り付けた商品と従来型の商品とで売上に違いがあるかどうかを調べたいときは，同一店舗の中で両方とも売ればよい．）
　しかし，上記の例では中学１年生の数学の授業は一生に１回きりのことなので，２人の人がお互いに影響せずに１人の生徒に教えることはできない．このような場合に，他の要因を等質化するために，入学時の得点が等しい対を選んでいる．（「初等統計学」［培風館/Ｐ．Ｇ．ホーエル著，浅井晃・村上正康訳］には，さらに他の教科の得点もほぼ似ている生徒の組を選ぶという例が示されている）
例５
　右の表５は異なる２人の担当者による１年間の授業の結果として，学年末の数学の得点に差異があるかどうかを調べたもので，Ｎｏ欄は生徒の対の整理番号，Ａ欄は担当者Ａに教えてもらった生徒の学年末の得点，Ｂ欄は担当者Ｂに教えてもらった生徒の学年末の得点とする．
　この表においては，中学入学時の診断テストの得点はどこにも表れていないことに注意．Ｎｏ1の対は40点と40点，Ｎｏ2の対は56点と56点，Ｎｏ3の対は65点と65点，...のように横に並んでいる２人の対ごとに診断テストの得点は等しいが，整理番号が異なる対では得点は一般には異なる（たまたま同じものがあるのはよい．）

※この例では，人的な属性（同一被験者，双生児，夫婦）とは全く無関係に対が選ばれている．
表５
No Ａ B
1 43 50
2 54 44
3 38 50
4 41 44
5 47 38
6 35 55
7 38 44
8 39 37
9 45 59
10 35 44
11 57 57
12 51 45
13 58 38

※このような比較においては，「異なる２人の担当者による授業」という要因以外の要因が可能な限り等しい方がよい．できれば，他の教科の得点もほぼ似ている方がよい･･･もっと言えば，出身小学校，男女別，学習塾に通っているかどうかなども各対について等しい方がよいが，このように条件を絞り過ぎると条件を満たすサンプルがなくなってしまう．
　そこで，対となるサンプルを選ぶときに考慮できない多くの要因については，無作為抽出による等質化を図る．ただし，この無作為抽出によって等質化できているかどうかは証明されないリスクを含んでいるので，考慮されなかった要因のうち何らかの要因が結果に影響するという有力な学説があれば，この分け方ではまずいことになる．そのような要因があれば，その要因の有無に応じて表３のように半数ずつ入れ替えてその効果を相殺する必要がある．

■Excelを使ったｔ検定
(1)
表１のデータを使って例１で述べた「対応のある場合のｔ検定」を行うには
上の表１のデータをExcelに転記するには，画面上でドラッグ→反転表示→右クリック→コピーしてから，Excel上で貼り付ける．（右の図１は解説用で，これをコピーすると行見出し（1～13），列見出し（A～C）の部分［灰色部分］が余計に入り１行１列ずつずれるので，コピーする場合は上の表１の方がよい．）
　Excelワークシートの左上端に，表１のデータが右図のようにできたとするとき，例１の両側検定を行うには
○１　最も簡単な方法として「分析ツール」を使う方法
Excel2002の場合
ツールのメニューに「分析ツール」がないときは，ツール→アドインで分析ツールにチェックを付けます．
ツール→分析ツール→ｔ検定：一組の標本による平均の検定→［ＯＫ］
→右図のようなダイアログ画面（対話型入力画面）になるので，変数1の入力範囲(1)にはB1:B13と書き込む（絶対参照の記号$マークは自動で入る），または，その入力欄の右にあるをクリックして，B1からB13までをドラッグする（表題B1も入れるか入れないかによって「ラベル」欄にチェックを入れるかどうかが変わる）
→変数2の入力範囲(1)にはC1:C13と書き込む（絶対参照の記号$マークは自動で入る），または，その入力欄の右にあるをクリックして，C1からC13までをドラッグする（表題C1も入れるか入れないかによって「ラベル」欄にチェックを入れるかどうかが変わるが，取り扱いは変数1にそろえる）
→帰無仮説との差異の欄は空欄のまま放置すれば，自動的に0が入り，「2つの変数の平均の差が0」（２つの変数が等しい）が帰無仮説となる．例えば，この欄に5を記入すると，「２つの変数の平均の差が5」を帰無仮説として「２つの変数の平均の差が5にならない」を対立仮説とすることになる.
→上の例のように変数1，2の入力範囲にＡ，Ｂというラベルも含めているときには，「ラベル」欄にチェックを入れる．（そうでないとき，B2:B13とC2:C13を変数の入力範囲にするときはチェックを入れない．ただし，ラベルがなければ作ってでも入力欄にラベルを含める方が結果は分かり易くなる．）
→有意水準5％の検定を行うときは，αとして0.05を書きこむ（％でなく小数で書く．）
→何度も検定を繰り返すような場合に，その都度新規ワークシートを増やしていくと，見づらく複雑になるのを防ぐには「出力オプション」を選んで，出力先セル（範囲というよりは左上の１つのセル番地）を指定するとよい．分析ツールでは指定されたセルから右下に14行3列の範囲に出力結果を書き込むので，右側下側が空欄になっているセルを指定する．（空欄になっていないとき「上書きする場合はＯＫを押してください」という警告が出て，あえて行うとそこにあったデータは上書きされてなくなる．）
→図３のように出力結果が書きこまれる．
片側検定のときは青色の背景色で示した部分を，両側検定のときは桃色の背景色で示した部分を読むことになる．
この例のようにＡ欄の平均がＢ欄の平均よりも大きい場合はｔ値が正になり，逆の場合はこれと符号だけが逆の負の値となるがそれ以外は同じものになるが，使うときは|ｔ|の値が背景色が青色または桃色で示した値よりも大きいかどうかで判断する．
この例では両側検定なので，桃色で示した欄を読み，ｔ境界値両側（両側検定で有意差が認められる境界値）が2.2...となるのに対して与えられたデータから計算したｔ値が1.39...だからｔ値が境界値よりも小さくＡ，Ｂ２群のデータが等しいという帰無仮説の採択域に落ちる．したがって，帰無仮説は棄却されず「有意差は認められない」．
→図５のようにまとめる．
有意差の有無の文章．（両側検定か片側検定か：ｔ（自由度）=ｔ値，ｐ値の範囲）　の順


Excel2007の場合
ツールのメニューに「分析ツール」がないときは，一番上左のExcelボタンを押して，（右下にある）Excelのオプション→アドイン→管理欄がExcelのアドインになっている状態で「設定」をクリック→分析ツールにチェックを付けてOK
データ→データ分析
から入り，以後の操作は上記に同じ
Excel2010の場合
ツールのメニューに「分析ツール」がないときは，一番上左のファイル→オプション→アドイン→（右下にある）Excelのオプション→アドイン→管理欄がExcelのアドインになっている状態で「設定」をクリック→分析ツールにチェックを付けてOK
データ→データ分析
から入り，以後の操作は上記に同じ
図１
　 A B C
1 Ｎｏ Ａ Ｂ
2 1 109 105
3 2 115 100
4 3 107 118
5 4 124 122
6 5 123 122
7 6 112 125
8 7 128 101
9 8 119 128
10 9 121 104
11 10 124 107
12 11 123 103
13 12 123 128
図２

図３
t-検定 : 一対の標本による平均の検定ツール
　 　 　
　 Ａ Ｂ
平均 119 113.5833333
分散 44.72727273 124.6287879
観測数 12 12
ピアソン相関 -0.081580568 　
仮説平均との差異 0 　
自由度 11 　
t 1.392640771 　
P(T<=t) 片側 0.095618425 　
t 境界値 片側 1.795883691 　
P(T<=t) 両側 0.191236851 　
t 境界値 両側 2.200986273 　

図４


図５
　･･･有意差は認められない．（両側検定：t(11)=1.39, p>.05）

※t(　)の中に書き込む数字は，データの組数12ではなく自由度で，データの組数-１=11になる．

分析ツールの出力として書きこまれた表は
1.　「元に戻す」ボタンによって戻すことはできない．（罫線だけは戻る）
2.　分析ツールで出力を書きこんだ後に元のデータを書き換えたとき，新たなデータに追随しない（更新されない）．

　表１から表５のようにデータそのものが与えられているときは，Excelの分析ツールを使って対応のあるｔ検定を行うことができるが，
２つの群について平均，標準偏差，相関係数などの要約データが与えられているときは，Excelの分析ツールではｔ検定はできない．
　必要な場合は，次の公式に値を代入して計算することとなる．（この頁参照）
○２　ワークシート関数を使ってｔ検定を行う方法
　図１のようにデータがあるとき，
(1)　ワークシート関数を直接入力するとき（Excel2002, 2007, 2010とも共通）
ｐ値を書きこみたいセルに
=TTEST(B2:B7,C2:C7,2,1)
と記入します．
　･･･［第３引数は両側検定のとき2，片側検定のとき1］
　･･･［第4引数は対応のある場合1，等分散が仮定できるとき2，非等分散のとき3］
※第1引数と第2引数の入力範囲にラベル(B1とC1)を含めるかどうか：ラベルが文字データ（Ａ、Ｂなど）であるときは=TTEST(B1:B7,C1:C7,2,1)のようにラベルを含めて指定しても同じ結果が得られる．ラベルが数値データ（1, 2など）であるときに，入力範囲にラベルも含めてしまうと間違った計算結果が出力される．（このワークシート関数によって返されるのは単なるｔ値なので，分析ツールの出力結果のようにラベルの有無によって読みやすさは変わらない．そこで，間違いを避けるためには，ラベルを含めずに入力範囲を指定するほうがよい．）
返される値はｔ検定を行ったときの出現確率：分析ツールで出力される P(T<=t) 両側 0.191236851 と同じ値となる．
このｐ値が p>0.05 となるから有意差はないと判断できる．


ワークシート関数 TTEST()を使ってｐ値を求めたときは，
　結果が得られて後に元のデータを書き換えたとき，新たなデータに追随する（ｐ値は更新される）．

　表１から表５のようにデータそのものが与えられているときは，Excelのワークシート関数を使って対応のあるｔ検定を行うことができるが，
２つの群について平均，標準偏差，相関係数などの要約データが与えられているときは，Excelの１つのワークシート関数ではｔ検定はできない．
　必要な場合は，次の公式に値を代入して計算することとなる．（この頁参照）
(2) 対話型メニューを使って関数を書きこむ場合（Excel2002, 2007, 2010とも共通）
　挿入→ワークシートの上端の上にあるfxをクリック→（関数の分類として統計を選択）TTEST→ＯＫ
（下図６の対話型メニューが表示される）→配列1にB2:B13（または，その入力欄の右にあるをクリックして，B2からB13までをドラッグする）；配列2にC2:C13（または，その入力欄の右にあるをクリックして，C2からC13までをドラッグする）；尾部には上記の第3引数の両側検定を表す2を書きこむ（この数値は選択するときにアシストとして表示される）；検定の種類には上記の第4引数の対応のある場合を表す1を書きこむ（この数値は選択するときにアシストとして表示される）→ＯＫ
図6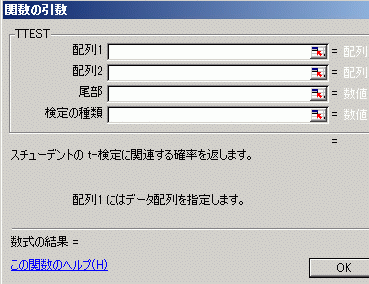

【問題１】表２のデータについて，このダイエット法には効果があるかとうか有意水準5％の片側検定で判断してください．
　データを転記するには，画面上でドラッグ→反転表示→右クリック→コピーしてから，Excel上に貼り付けるとよい．
　次の空欄を埋めてください．
（小数第３位を四捨五入して小数第２位まで答えるものとする）
○
t=
片側検定のｔ境界値は
上記２つの数値を比較して，|t|がｔ片側境界値よりも大きいことから有意水準5％で有意差がある．

○（または，次のようにｐ値を見るだけで判断してもよい．）
p=<0.05
だから有意水準5％で有意差がある．
採点する やり直す

【問題２】表３のデータについて，２つの指導法による得点の有意差があるかどうか有意水準5％の両側検定で判断してください．
　データを転記するには，画面上でドラッグ→反転表示→右クリック→コピーしてから，Excel上で貼り付けるとよい．
　次の空欄を埋めてください．
（小数第３位を四捨五入して小数第２位まで答えるものとする）
○
t=
両側検定のｔ境界値は
上記２つの数値を比較して，|t|がｔ片側境界値よりも小さいことから有意水準5％で有意差はない．

○（または，次のようにｐ値を見るだけで判断してもよい．）
p=>0.05
だから有意水準5％で有意差はない．
採点する やり直す

【問題３】表４のデータについて，Ａ，Ｂの母集団平均に有意差があるかどうか有意水準5％の両側検定で判断してください．
　データを転記するには，画面上でドラッグ→反転表示→右クリック→コピーしてから，Excel上で貼り付けるとよい．
　次の空欄を埋めてください．
（小数第３位を四捨五入して小数第２位まで答えるものとする）
○
t=
両側検定のｔ境界値は
上記２つの数値を比較して，|t|がｔ片側境界値よりも小さいことから有意水準5％で有意差はない．

○（または，次のようにｐ値を見るだけで判断してもよい．）
p=>0.05
だから有意水準5％で有意差はない．
採点する やり直す

【問題４】表５のデータについて，Ａ，Ｂの母集団平均に有意差があるかどうかTTEST関数を使って有意水準5％の両側検定で判断してください．
　データを転記するには，画面上でドラッグ→反転表示→右クリック→コピーしてから，Excel上で貼り付けるとよい．
　次の空欄を埋めてください．
（小数第３位を四捨五入して小数第２位まで答えるものとする）
○
p=>0.05
だから有意水準5％で有意差はない．
採点する やり直す

①Excel2007～2010, web上にあるフリーのExcel onlineで行う場合
②フリーの統計ソフトRで行う場合
*** 作業例 ***
表１
Ｎｏ Ａ Ｂ
1 109 105
2 115 100
3 107 118
4 124 122
5 123 122
6 112 125
7 128 101
8 119 128
9 121 104
10 124 107
11 123 103
12 123 128
【例1】
　右の表１は定期健診での12人の最高血圧の一覧表であるものとする．
　No欄は被験者の整理番号，Ａ欄は昨年の定期検査時の最高血圧，Ｂ欄は今年の定期検査時の最高血圧とする．
　この検診で昨年と今年で最高血圧に有意差があるかどうか，両側検定で調べてください．
①Excelの分析ツールを使う場合
データ→データ分析→一対の標本による平均の検定
⇒次のように出力される
	Ａ	Ｂ
平均	119	113.583..
分散	44.727..	124.628..
観測数	12	12
ピアソン相関	-0.081..	
仮説平均との差異	0	
自由度	11	
t 	1.392..	
P(T<=t) 片側	0.095..	
t 境界値 片側	1.795..	
P(T<=t) 両側	0.191..	
t 境界値 両側	2.200..
⇒p値=0.191>0.05だから有意差は認められない．または，t値=1.39<2.20だから有意差は認められない．
【結果のまとめ方】
　表１は，被験者12人について，昨年と今年の最高血圧の平均と分散を示したものである．(N=12)
《表1》 最高血圧の平均と分散
昨年今年
平均119113.6
分散44.7124.6
「ｔ検定の結果，両条件の平均の差は有意でなかった（両側検定：t(11)=2.20, p=.19）．したがって，昨年と今年で最高血圧に有意差は認められない．」
①Excelのワークシート関数で行う場合
　ワークシート関数は1つの関数が１つの結果を返すため，この問題のように7個の値が必要な場合には，関数を７個書く必要があり，それなりに大変である．
　しかし，ワークシート関数から得られる結果は，元データが更新された場合に，リアルタイムで結果が追随するという良さはある．
　別ルートから計算しているので，点検作業という意味はある．
=T.TEST(A群の範囲, B群の範囲, 2,1)により0.191が得られる
• 第3引数は，2が両側検定を表す
• 第4引数は，1が対応のある検定
=TINV(上記で得られるp値,自由度)により1.39が得られる
• p値だけでも判断できるがｔ値を求めるにはこうするとよい • 自由度は対の数−1，この問題では11になる
=TINV(0.05,自由度)により2.20が得られる
• t値の両側境界線を求める
=AVERAGE(A群の範囲), =AVERAGE(B群の範囲), =VAR(A群の範囲), =VAR(B群の範囲)
• 各々の群の平均と分散を求める
【結果のまとめ方】
　前述と同様
②Rで行う場合
各群のデータをベクトルとして入力する
• t.test( )の第３引数をpaired=TRUEとする
• t.tset( )の第４引数を，
両側検定ならば alternative="two.sided"，
左側が小さい片側検定ならば alternative="less"，
左側が大きい片側検定ならば alternative="greater"
とする（上記のTRUEとは異なり引用符に囲まれた"文字列"として"less", "greater"を書く．
alternative=を省略すれば両側検定"two.sided"になる．）
> a<-c(109,115,107,124,123,112,128,119,121,124,123,123)
> b<-c(105,100,118,122,122,125,101,128,104,107,103,128)
> t.test(a,b,paired=TRUE)

        Paired t-test

data:  a and b
t = 1.3926, df = 11, p-value = 0.1912
alternative hypothesis: true difference in means
 is not equal to 0
95 percent confidence interval:
 -3.14405 13.97738
sample estimates:
mean of the differences 
               5.416667
⇒p値=0.191>0.05だから有意差は認められない．または，95%信頼区間に「0」が含まれるから平均値が等しいという仮定は棄却されない
Rでt検定の境界値を求めるには，関数qt( )を使う．
qt(確率:p値, 自由度, lower.tail=..)⇒t値
とする．
• 第１引数の確率は省略できない．小数で書く．両側検定で5%となる境界線を求めるには，確率を0.025とする
• 第２引数は自由度．12対のデータの自由度は11
• 上側確率，下側確率は，引数の位置ではなくlower.tailという名前タグによって指定する．省略すればlower.tail=TRUEとなって下側確率を返す．上側確率を返すにはlower.tail=FALSEとする．
この問題では，qr(0.025, 11, lower.tail=FALSE)により，5%両側検定の上側境界線のt値2.20が得られる．
【結果のまとめ方】
　前述と同様

No A前 B後
1 54.3 52.6
2 51.9 48.7
3 55.2 56.7
4 55.3 52.5
5 53.8 52.1
6 52.1 53.3
7 53.6 51.4
8 50.2 49.2
【例2】
　右の表はあるダイエット法を行う前と後の体重の一覧表であるものとする．No欄は被験者の整理番号，Ａ欄は実施前の体重，Ｂ欄は実施後の体重とする．
　表からこのダイエット法には効果があったと言えるかどうか片側検定で判断してください．
①Excelの分析ツールを使う場合
データ→データ分析→一対の標本による平均の検定
⇒次のように出力される
t-検定: 一対の標本による平均の検定ツール
	前	後
平均	53.3	52.062..
分散	3.137..	6.208..
観測数	8	8
ピアソン相関	0.716..	
仮説平均との差異	0	
自由度	7	
t 	2.014..	
P(T<=t) 片側	0.041..
t 境界値 片側	1.894..	
P(T<=t) 両側	0.083..
t 境界値 両側	2.364..
⇒p値=0.041<0.05だから有意差がある．
または，t値=2.014>1.894だから有意差がある．
【結果のまとめ方】
　表1は，被験者8人について，ダイエット法実施の前後の平均体重と分散を示したものである．(N=8)
《表1》 前後の平均体重と分散
前後
平均53.3 *52.1 *
分散3.146.21
「ｔ検定の結果，平均体重の差は有意であった（片側検定：t(7)=2.014, p=.041）．したがって，このダイエット法のよる体重の減少が認められる．」
*p<.05, **p<.01
 ①Excelのワークシート関数を使う場合
=T.TEST(前の体重範囲, 後の体重の範囲, 1,1)により0.041..が得られる
• 第3引数は，1が片側検定を表す
• 第4引数は，1が対応のある検定
=TINV(上記の確率p値×2,自由度)により1.39が得られる
• p値だけでも判断できるがｔ値を求めるにはこうするとよい.
（#注#）TINV(p値,自由度)とすると，両側確率がp値となるｔ値が返されるが，片側だけでp値となるt値を求めるには，面積が２倍のp値に対応するtを求めると合う
• 自由度は対の数−1，この問題では7になる
=TINV(0.05×2,自由度)により1.89..が得られる
• t値の片側境界線を求める
=AVERAGE(A群の範囲), =AVERAGE(B群の範囲), =VAR(A群の範囲), =VAR(B群の範囲)
• 各々の群の平均と分散を求める
【結果のまとめ方】
　前述と同様
②Rで行う場合
各群のデータをベクトルとして入力する
• t.test( )の第３引数をpaired=TRUEとする
• t.tset( )の第４引数を，
両側検定ならば alternative="two.sided"，
左側が小さい片側検定ならば alternative="less"，
左側が大きい片側検定ならば alternative="greater"
とする（上記のTRUEとは異なり引用符に囲まれた"文字列"として"less", "greater"を書く．
alternative=を省略すれば両側検定"two.sided"になる．）
> before<-c(54.3,51.9,55.2,55.3,53.8,52.1,53.6,50.2)
> after<-c(52.6,48.7,56.7,52.5,52.1,53.3,51.4,49.2)
> t.test(before,after,paired=TRUE,alternative="greater")

        Paired t-test

data:  before and after
t = 2.0142, df = 7, p-value = 0.04192
alternative hypothesis: true difference
 in means is greater than 0
95 percent confidence interval:
 0.07348583        Inf
sample estimates:
mean of the differences 
                 1.2375
⇒p値=0.041<0.05だから有意差が認められる．または，95%信頼区間に「0」が含まれないから平均値が等しいという仮定は棄却される．
　t検定の境界値も求めるには，関数qt( )を使う．
qt(0.05, 7, lower.tail=FALSE)により，5%片側検定の上側境界線のt値 1.89..が得られる．
【結果のまとめ方】
　前述と同様

①Excel2007～2010, web上にあるフリーのExcel onlineで行う場合
②フリーの統計ソフトRで行う場合
*** 作業例 ***
表１
Ｎｏ Ａ Ｂ
1 109 105
2 115 100
3 107 118
4 124 122
5 123 122
6 112 125
7 128 101
8 119 128
9 121 104
10 124 107
11 123 103
12 123 128
【例1】
　右の表１は定期健診での12人の最高血圧の一覧表であるものとする．
　No欄は被験者の整理番号，Ａ欄は昨年の定期検査時の最高血圧，Ｂ欄は今年の定期検査時の最高血圧とする．
　この検診で昨年と今年で最高血圧に有意差があるかどうか，両側検定で調べてください．
①Excelの分析ツールを使う場合
データ→データ分析→一対の標本による平均の検定
⇒次のように出力される
	Ａ	Ｂ
平均	119	113.583..
分散	44.727..	124.628..
観測数	12	12
ピアソン相関	-0.081..	
仮説平均との差異	0	
自由度	11	
t 	1.392..	
P(T<=t) 片側	0.095..	
t 境界値 片側	1.795..	
P(T<=t) 両側	0.191..	
t 境界値 両側	2.200..
⇒p値=0.191>0.05だから有意差は認められない．または，t値=1.39<2.20だから有意差は認められない．
【結果のまとめ方】
　表１は，被験者12人について，昨年と今年の最高血圧の平均と分散を示したものである．(N=12)
《表1》 最高血圧の平均と分散
昨年今年
平均119113.6
分散44.7124.6
「ｔ検定の結果，両条件の平均の差は有意でなかった（両側検定：t(11)=2.20, p=.19）．したがって，昨年と今年で最高血圧に有意差は認められない．」
①Excelのワークシート関数で行う場合
　ワークシート関数は1つの関数が１つの結果を返すため，この問題のように7個の値が必要な場合には，関数を７個書く必要があり，それなりに大変である．
　しかし，ワークシート関数から得られる結果は，元データが更新された場合に，リアルタイムで結果が追随するという良さはある．
　別ルートから計算しているので，点検作業という意味はある．
=T.TEST(A群の範囲, B群の範囲, 2,1)により0.191が得られる
• 第3引数は，2が両側検定を表す
• 第4引数は，1が対応のある検定
=TINV(上記で得られるp値,自由度)により1.39が得られる
• p値だけでも判断できるがｔ値を求めるにはこうするとよい • 自由度は対の数−1，この問題では11になる
=TINV(0.05,自由度)により2.20が得られる
• t値の両側境界線を求める
=AVERAGE(A群の範囲), =AVERAGE(B群の範囲), =VAR(A群の範囲), =VAR(B群の範囲)
• 各々の群の平均と分散を求める
【結果のまとめ方】
　前述と同様
②Rで行う場合
各群のデータをベクトルとして入力する
• t.test( )の第３引数をpaired=TRUEとする
• t.tset( )の第４引数を，
両側検定ならば alternative="two.sided"，
左側が小さい片側検定ならば alternative="less"，
左側が大きい片側検定ならば alternative="greater"
とする（上記のTRUEとは異なり引用符に囲まれた"文字列"として"less", "greater"を書く．
alternative=を省略すれば両側検定"two.sided"になる．）
> a<-c(109,115,107,124,123,112,128,119,121,124,123,123)
> b<-c(105,100,118,122,122,125,101,128,104,107,103,128)
> t.test(a,b,paired=TRUE)

        Paired t-test

data:  a and b
t = 1.3926, df = 11, p-value = 0.1912
alternative hypothesis: true difference in means
 is not equal to 0
95 percent confidence interval:
 -3.14405 13.97738
sample estimates:
mean of the differences 
               5.416667
⇒p値=0.191>0.05だから有意差は認められない．または，95%信頼区間に「0」が含まれるから平均値が等しいという仮定は棄却されない
Rでt検定の境界値を求めるには，関数qt( )を使う．
qt(確率:p値, 自由度, lower.tail=..)⇒t値
とする．
• 第１引数の確率は省略できない．小数で書く．両側検定で5%となる境界線を求めるには，確率を0.025とする
• 第２引数は自由度．12対のデータの自由度は11
• 上側確率，下側確率は，引数の位置ではなくlower.tailという名前タグによって指定する．省略すればlower.tail=TRUEとなって下側確率を返す．上側確率を返すにはlower.tail=FALSEとする．
この問題では，qr(0.025, 11, lower.tail=FALSE)により，5%両側検定の上側境界線のt値2.20が得られる．
【結果のまとめ方】
　前述と同様

No A前 B後
1 54.3 52.6
2 51.9 48.7
3 55.2 56.7
4 55.3 52.5
5 53.8 52.1
6 52.1 53.3
7 53.6 51.4
8 50.2 49.2
【例2】
　右の表はあるダイエット法を行う前と後の体重の一覧表であるものとする．No欄は被験者の整理番号，Ａ欄は実施前の体重，Ｂ欄は実施後の体重とする．
　表からこのダイエット法には効果があったと言えるかどうか片側検定で判断してください．
①Excelの分析ツールを使う場合
データ→データ分析→一対の標本による平均の検定
⇒次のように出力される
t-検定: 一対の標本による平均の検定ツール
	前	後
平均	53.3	52.062..
分散	3.137..	6.208..
観測数	8	8
ピアソン相関	0.716..	
仮説平均との差異	0	
自由度	7	
t 	2.014..	
P(T<=t) 片側	0.041..
t 境界値 片側	1.894..	
P(T<=t) 両側	0.083..
t 境界値 両側	2.364..
⇒p値=0.041<0.05だから有意差がある．
または，t値=2.014>1.894だから有意差がある．
【結果のまとめ方】
　表1は，被験者8人について，ダイエット法実施の前後の平均体重と分散を示したものである．(N=8)
《表1》 前後の平均体重と分散
前後
平均53.3 *52.1 *
分散3.146.21
「ｔ検定の結果，平均体重の差は有意であった（片側検定：t(7)=2.014, p=.041）．したがって，このダイエット法のよる体重の減少が認められる．」
*p<.05, **p<.01
 ①Excelのワークシート関数を使う場合
=T.TEST(前の体重範囲, 後の体重の範囲, 1,1)により0.041..が得られる
• 第3引数は，1が片側検定を表す
• 第4引数は，1が対応のある検定
=TINV(上記の確率p値×2,自由度)により1.39が得られる
• p値だけでも判断できるがｔ値を求めるにはこうするとよい.
（#注#）TINV(p値,自由度)とすると，両側確率がp値となるｔ値が返されるが，片側だけでp値となるt値を求めるには，面積が２倍のp値に対応するtを求めると合う
• 自由度は対の数−1，この問題では7になる
=TINV(0.05×2,自由度)により1.89..が得られる
• t値の片側境界線を求める
=AVERAGE(A群の範囲), =AVERAGE(B群の範囲), =VAR(A群の範囲), =VAR(B群の範囲)
• 各々の群の平均と分散を求める
【結果のまとめ方】
　前述と同様
②Rで行う場合
各群のデータをベクトルとして入力する
• t.test( )の第３引数をpaired=TRUEとする
• t.tset( )の第４引数を，
両側検定ならば alternative="two.sided"，
左側が小さい片側検定ならば alternative="less"，
左側が大きい片側検定ならば alternative="greater"
とする（上記のTRUEとは異なり引用符に囲まれた"文字列"として"less", "greater"を書く．
alternative=を省略すれば両側検定"two.sided"になる．）
> before<-c(54.3,51.9,55.2,55.3,53.8,52.1,53.6,50.2)
> after<-c(52.6,48.7,56.7,52.5,52.1,53.3,51.4,49.2)
> t.test(before,after,paired=TRUE,alternative="greater")

        Paired t-test

data:  before and after
t = 2.0142, df = 7, p-value = 0.04192
alternative hypothesis: true difference
 in means is greater than 0
95 percent confidence interval:
 0.07348583        Inf
sample estimates:
mean of the differences 
                 1.2375
⇒p値=0.041<0.05だから有意差が認められる．または，95%信頼区間に「0」が含まれないから平均値が等しいという仮定は棄却される．
　t検定の境界値も求めるには，関数qt( )を使う．
qt(0.05, 7, lower.tail=FALSE)により，5%片側検定の上側境界線のt値 1.89..が得られる．
【結果のまとめ方】
　前述と同様

■［個別の頁からの質問に対する回答］[対応のある場合のｔ検定について／17.8.2］対応のあるt検定について教えてください。 preとpostで変化があったのかを分析するとした場合についてお伺いします。 preが正規分布していて、postが正規分布していなかった場合は、対応のあるt検定をせずとも「変化があり」と結論付けて良いのでしょうか。 対応があるにもかかわらず分布が変わっているということは、変化があったということとニアリーイコールだと思います。

＝＞［作者］：連絡ありがとう．どちらかと言えば，筆者があまり得意としていない分野なので，たぶんというレベルの話として･･･そもそもｔ検定は母集団が正規分布をなすことを前提としているので，実験群か統制群（比較群）のいずれか一方が正規分布をなしていなければ，そもそもｔ検定による有意差検定はできないのではないか．順序相関など正規分布を前提としない分析方法がよいと思いますが･･･
確率統計のメニューに戻る 高校数学のメニューに戻る