|
■考え方
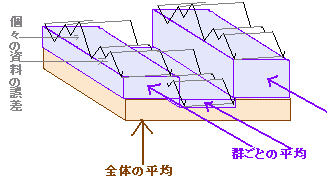
◇一元配置法のイメージ◇ 資料の値の変動は,右図のように群(グループ,列,級)間の変動と個々の資料の群内変動(誤差による変動)に分けられる.すなわち,個々の値:yij ,列平均: yij - そこで, (この場合,通常のF値の扱いと異なり,大きい方を分子にするのでなく,必ず群間の不偏分散を分子とする.右図参照) |
  |
|
|
■分散分析・・・3つ以上の母集団の平均の差の検定 ○ 2つの母集団の平均値に有意差があるかどうかはF検定→t検定で調べることができるが,3つ以上の集団について2つずつ取り出してテストしていたのでは組合わせが多く大変である. ○ 3つ以上の母集団について平均値に有意差があるかどうかを調べる方法として,分散分析がある. ○ 結果に影響を及ぼす様々な要因のうちで,他の要因は変えずに1つの要因の違いだけに着目して,その平均値に有意差があるかどうか調べるものを「一元配置法」(1因子の分散分析)という.・・・表1参照 ○ 2つの要因の組合わせを考えるものを「二元配置法」(2因子の分散分析)といい,二元配置法には「繰り返しのない二元配置」と「繰り返しのある二元配置」(・・・表2参照)がある. |
表1
|
|
■考え方
◇一元配置法のイメージ◇ 資料の値の変動は,右図のように群(グループ,列,級)間の変動と個々の資料の群内変動(誤差による変動)に分けられる.すなわち,個々の値:yij ,列平均: yij - そこで, (この場合,通常のF値の扱いと異なり,大きい方を分子にするのでなく,必ず群間の不偏分散を分子とする.右図参照) |
  |
|
|
■Excelでの操作 ◇一元配置法◇ ○ 定義に従って表を組み立てるとき:(実務は分析ツールがお薦め) 右の表3のようなデータがあるとき,平均値の差は簡単に分かるがそれが有意差なのか,誤差の範囲程度のものなのかを判断するには: (1) 群ごとの平均,全体平均を計算する: B11に =AVERAGE(B2:B9)・・・数値が入力されたセルのみの平均 D11までコピー・貼り付け E11に =AVERAGE(B2:D9) (2) 群内変動(誤差による変動)を計算する: B13に =(B2-B$11)^2 これを空白セル以外にコピー・貼り付け (C列では =(C2-C$11)^2 などとなる) 列ごとの和を求める:B21に =SUM(B13:B20) D21までコピー・貼り付け E21に横の和 =SUM(B21:D21) 群内変動の不偏分散を求めるとき,自由度は(標本数)-(この計算に用いる平均値の個数)=(7+6+5)-3=15 とする. 以上により,群内変動の不偏分散=63.1/15=4.20 上記(1)(2)の短縮法:各群の標本数をp,q,rとするとき,各不偏分散は(3) 群間変動を計算する: (各群の平均-全体平均)2 を求めて,列ごとに和を求めるが,右の表のようにこの値は列ごとに一定だから, (各群の平均-全体平均)2 ×(標本数)でよい. ・・・・標本数を掛けることが重要 次に,群間変動の不偏分散を求めるときに,その計算に用いた新たな平均値は全体平均1個だから,自由度=群の個数-1=2 以上により,群間変動の不偏分散=群間変動/2=26.32 (4) F値を求める: F = 26.32/4.20 = 6.26 ※ 右のような分散分析表にまとめる. (5) F検定で判断する: =FINV(0.05, 分子自由度2,分母自由度15) = 3.68<6.26 により 群ごとの平均値に有意差がある. または =FDIST(F値 6.26, 分子自由度2,分母自由度15) = 0.01<0.05により群ごとの平均値に有意差がある. ○ 分析ツールを用いるとき:(実務向き) (空白データが含まれるのはよいが,「欠席」などと文字列が記入してある場合,分析ツールは使えないので空白とする.) ツール→分析ツール→分散分析:一元配置 入力範囲を 上の表3の水色で示した範囲とする.(この場合は「先頭行をラベルとして使用」にチェックを入れる.) ==> 右の表4のように出力される. 各々の数値と上の解説とは文字色により対応を示した. 【要点】 P-値0.01が0.05よりも小さいから有意差ありと判断する. または 観測された分散比6.26>F境界値3.68だから有意差ありと判断する. |
表3
表4
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
◇繰り返しのない二元配置法◇ 2つの要因を同時に変化させた幾つかの観測結果から,各々の要因が及ぼす影響を判断する・・・例えば,温度と塩分濃度の両方を変化させてバクテリアの増加を観測する,4種類の苗を3箇所に植えて成長を観察する,など. 個々の値を ここで, (列の効果)=(列の平均)-(全体の平均) (行の効果)=(行の平均)-(全体の平均) (誤差)=(個々の値)-(全体の平均)-(列の効果)-(行の効果) で定義する. 次に, 列間の分散比=列間不偏分散/誤差の不偏分散 行間の分散比=行間不偏分散/誤差の不偏分散 により,列,行の平均値に有意差があるかどうか判断する. |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ○ 定義に従って表を組み立てるとき:(実務は分析ツールがお薦め) 右の表5のような元データがあるとき: (1) 行平均,列平均,全体平均を求める. (2) (行の効果)=(行平均)-(全体平均) の表を右側に作る.(この値は,各行で等しい) (3) (列の効果)=(列平均)-(全体平均) の表を下側に作る.(この値は,各列で等しい) (4) (誤差)=(元の値)-(全体平均)-(行の効果)-(列の効果) の表を右下に作る. (5) 行変動の2乗和 を計算し,行変動の欄に書き込む B15 に =SUMSQ(H2:J5) 行変動の自由度の計算に当り,変数は4個,使用した平均値は全体平均の1個だから自由度は3(行数-1) ※行平均の不偏分散 =VAR(G2:G5) から計算するときは,3倍することが重要. 行の不偏分散は0.162/3=0.054 (6) 列変動の2乗和 を計算し,列変動の欄に書き込む B16 に =SUMSQ(B10:D13) 列変動の自由度の計算に当り,変数は3個,使用した平均値は全体平均の1個だから自由度は2(列数-1) ※列平均の不偏分散 =VAR(B7:D7) から計算するときは,4倍することが重要. 列の不偏分散は1.598/2=0.799 (7) 誤差の2乗和 を計算し,誤差変動の欄に書き込む B17 に =SUMSQ(H10:J13) 誤差変動の自由度の計算に当り,変数は3×4=12個,使用した平均値は周辺値として行平均が4個,列平均は3個,さらに全体平均が1個あるから,自由度=12-3-2-1=6 誤差の不偏分散は0.511/6=0.085 (8) 列間の分散比=列間不偏分散/誤差の不偏分散=0.63 5%F値は=FINV(0.05,3,6) = 4.76 0.63<4.76で有意差なし または =FDIST(E15,3,6) = 0.6198>0.05により有意差なし 行間の分散比=行間不偏分散/誤差の不偏分散=9.37 5%F値は=FINV(0.05,2,6) = 5.14>4.76で有意差あり または =FDIST(E16,2,6) = 0.0143<0.05で有意差あり |
表5
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ○ 分析ツールを用いるとき:(実務向き) ※ 標本数が異なるとき(空欄を含むとき)不可 ツール→分散ツール→分散分析:繰り返しのない二元配置 入力範囲:A1:D5(左欄のラベル,上欄のラベルとも入れてよい.このときは「ラベル」にチェックを付ける.) ラベル:チェック 右のように出力される(小数点以下の桁数はもう少し多い). 主な数値の上記「定義に従った計算」との対応は,同じ文字色で示した. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ◇繰り返しのある二元配置法◇ 右の表6のように教科と組別の2つの要因があって,それらの組合わせ(1組の英語など)ごとに繰り返し試験が行われたとする. このとき,教科の要因は英語・数学の2つの値をとり水準は2となり,組別の要因は1組・2組の2つの値をとり水準は2となる.また,これらの各組合わせについて,上から順に1回目,2回目,・・の計4回の試験が行われているので,「繰り返し数」は4となる. このようなデータの分散分析を「繰り返しのある二元配置法」という. 「繰り返しのある二元配置法」では,「繰り返しのない二元配置法」の場合に加えて,さらに,交互作用の効果を分析することができる. 組別の平均点の差が列の主効果として,教科の平均点の差が行の主効果として得られるのは,「繰り返しのない二元配置法」と同じであるが,これらの組合わせ・・・例えば,1組の数学・・・に,組別,教科別の効果だけでは説明できない得点の増減が見られる場合に,これを交互作用の効果という. 右図1のように,個々の値を (全体の平均)+(列の効果)+(行の効果)+(交互作用の効果)+(誤差)
に分けて考える.ここで, (列の効果)=(列の平均)-(全体の平均) (行の効果)=(行の平均)-(全体の平均) (交互作用の効果)=(小ブロックの平均)-(全体平均)-(列の効果)-(行の効果) (誤差)=(個々の値)-(全体の平均)-(列の効果)-(行の効果)-(交互作用の効果) で定義する. 次に, 行の分散比=行の不偏分散/誤差の不偏分散 列の分散比=列の不偏分散/誤差の不偏分散 交互作用の分散比=交互作用の不偏分散/誤差の不偏分散 により,行,列,交互作用の平均値に有意差があるかどうか判断する. |
表6
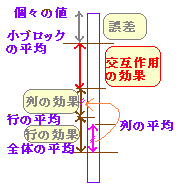 ※次のように定義しても同じ結果が得られる. ※ 「1組・英語」のような小ブロックの平均-全体平均 のうち,「行の効果」「列の効果」を取り除いたものが「交互作用の効果」となる. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
○ 定義に従って表を組み立てるとき:(実務は分析ツールがお薦め) 右の表7のような元データがあるとき, (1) 小ブロックごと,行ごと,列ごと,全体の平均を求めておく.(表8) ※ 以下の表は同一数値が繰り返し現われ冗長であるが,イメージ作りのためなので実際の計算は「×個数」で済ませることができる.計算内容を一度確認すれば,以後は,分析ツールだけでよい. (2) 表9のように(小ブロックの平均)-(全体平均)の表を作る・・・この数値は各小ブロックごとに同じ数値となる. 例 B12〜B15 =$F$2-$H$4 (3) 表10のように(組別平均)-(全体平均)の表を作る・・・・・・この数値は組別に同じ数値となる. 例 B22〜B29 =F$4-$H$4 (4) 表11のように(教科平均)-(全体平均)の表を作る・・・・・・この数値は教科ごとに同じ数値となる. 例 B32〜C35 =$H$2-$H$4 (5) 表12のように (小ブロックの平均)-(全体平均)-(教科の効果)-(組別の効果)の表を作る・・・・・・この数値は小ブロックごとに同じ数値となる. 例 B42 =B12-B22-B32 以下は,相対参照のコピー・貼り付けでできる. (6) 表13のように (元の値)-(全体の平均)-(教科の効果)-(組別の効果)-(交互作用の効果)の表を作る. 例 B52 =B2-$H$4-B22-B32-B42 以下は,相対参照のコピー・貼り付けでできる. (7) 表14のように分散分析表をまとめる. i) 教科の主効果の平方和 B62に =SUMSQ(B32:C39) ii) 組別の主効果の平方和 B63に =SUMSQ(B22:C29) iii) 交互作用の効果の平方和 B64に =SUMSQ(B42:C49) iv) 誤差の平方和 B65に =SUMSQ(B52:C59) v) 自由度については: 教科の変数は2個で,教科の効果の平方和計算には,(教科平均)-(全体平均)で全体平均を使うから,教科の自由度は2-1=1 組別の変数は2個で,組別の効果の平方和計算には,(組別平均)-(全体平均)で全体平均を使うから,組別の自由度は2-1=1 誤差の変数は16個で,誤差の平方和計算には,(誤差)=(個々の値)-(小ブロックの平均)で4個の平均を使うから,誤差の自由度は16-4=12 全体の変数は16個で,全体の平方和は,(個々の値)-(全体平均)で全体平均を使うから,全体の自由度は16-1=15 交互作用の自由度は,全体から差し引いても求められるが,(教科の自由度)×(組別の自由度)=1という説明が普通 vi) 教科の主効果,組別の主効果,交互作用の効果,誤差の各々について平方和÷自由度により不偏分散を求める. vii) 教科の主効果,組別の主効果,交互作用の効果の各々について誤差の不偏分散との比を求める.(これがF値) viii) 比較すべき5%F値は 教科の主効果では =FINV(0.05, 教科の自由度 1, 誤差の自由度 12) = 4.75 ここで0.85<4.75により教科の主効果は有意差なし. または, p値を =FDIST(F値0.85, 教科の自由度 1, 誤差の自由度 12) で求めて 0.37>0.05により有意差なし. 組別の主効果では =FINV(0.05, 組別の自由度 1, 誤差の自由度 12) =4.75 ここで0.39<4.75により教科の主効果は有意差なし. または, p値を =FDIST(F値0.39, 組別の自由度 1, 誤差の自由度 12) で求めて 0.55>0.05により有意差なし. 交互作用の効果では =FINV(0.05, 交互作用の自由度 1, 誤差の自由度 12) = 4.75 ここで10.14>4.75により交互作用の効果は有意差あり. または, p値を =FDIST(F値10.14, 交互作用の自由度 1, 誤差の自由度 12) で求めて 0.01<0.05により有意差あり. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ○ 分析ツールを用いるとき:(実務向き) ※ 標本数が異なるとき(空欄を含むとき)不可 ※ Excelの分析ツールで繰り返しのある二元配置法を行うには,右の表15のように繰り返しのデータが列方向に(何行分という形で)並ぶ必要があります. ツール→分散ツール→分散分析:繰り返しのある二元配置 入力範囲:A1:C9(左欄のラベル,上欄のラベルとも入れる) 1標本当りの行数:4 α:0.05 右の表16のように出力される(小数点以下の桁数はもう少し多い). 上記の「定義に従った計算」は,この出力形式にほぼ対応させたものである. |
表15
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
※ 分散分析について,分かりやすい記述のある書物
|