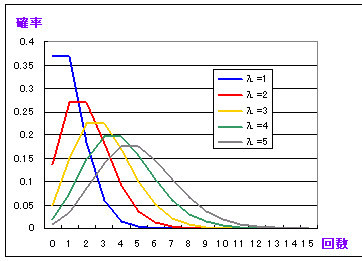
(3) カイ2乗検定[ポアソン分布との適合性]
次の表Aは,1997年から2006年までの120か月間に発生した台風237個(平均1.975回/月)について,各月の発生回数と月数を表にしたものである.
[データの出所:気象庁>気象統計情報 http://www.data.jma.go.jp]
平均1.975回のポアソン分布と見なした場合の発生回数は,表Bのようになる.
このとき,月ごとの台風の発生回数はポアソン分布に従うと見なしてよいかどうか検定せよ.(なお,ポアソン分布曲線は無限に長い尾になっており,10回以上の理論月数もあり得るため,9回までの合計は120ちょうどにはならない.)
表A
| 回数 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
計 |
| 観測月数 |
38 |
20 |
23 |
15 |
5 |
11 |
6 |
1 |
1 |
0 |
120 |
表B
| 回数 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
計 |
| 理論月数 |
16.65 |
32.88 |
32.47 |
21.37 |
10.55 |
4.16 |
1.37 |
0.38 |
0.09 |
0.02 |
… |
|
| 回数 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
計 |
| 観測月数 |
38 |
20 |
23 |
15 |
5 |
11 |
6 |
1 |
1 |
0 |
120 |
| 理論月数 |
16.65 |
32.88 |
32.47 |
21.37 |
10.55 |
4.16 |
1.37 |
0.38 |
0.09 |
0.02 |
119.94 |
| |
|
|
|
|
|
|
|
|
|
|
カイ2乗 |
| |
27.38 |
5.05 |
2.76 |
1.90 |
2.92 |
11.25 |
15.65 |
1.01 |
9.20 |
0.02 |
77.13 |
次のいずれかによる.
○ CHITEST(観測度数の範囲,期待度数の範囲) = 0.000 < 0.05 により帰無仮説棄却:有意差がある.
○ CHIDIST(カイ2乗,自由度9) = 0.000 < 0.05
により帰無仮説棄却:有意差がある.
○ CHIINV(0.05,自由度9) = 16.92 < カイ2乗 77.13
により帰無仮説棄却:有意差がある.
以上により,ポアソン分布には適合しない.
※ 台風は夏から秋に多く発生しており,年間を通してランダムに発生しているわけではない.
|
|
.
(4) カイ2乗検定[ポアソン分布との適合性]
あるコンビニでは,午前9時〜午後7時までの10時間に10分間当り平均2人の来客があり,各10分ごとの実際の来客数を調査したとき次の表のようになった.(架空データ)
この人数と回数の対応はポアソン分布に従うと見なしてよいか.
| 人数 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
計 |
| 回数 |
5 |
12 |
18 |
8 |
11 |
4 |
1 |
1 |
0 |
60 |
|
ポアソン分布に基づく確率=POISSON(イベント数,平均,0)に総数60を掛けると,期待度数が得られる.イベント数には,表中の人数を指定する.
| 人数 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
計 |
| 観測度数 |
5 |
12 |
18 |
8 |
11 |
4 |
1 |
1 |
0 |
60 |
| 期待度数 |
8 |
16 |
16 |
11 |
5 |
2 |
1 |
0 |
0 |
60 |
| |
|
|
|
|
|
|
|
|
|
カイ2乗 |
| |
1.20 |
1.11 |
0.19 |
0.74 |
5.77 |
1.55 |
0.11 |
3.06 |
0.05 |
13.77 |
次のいずれかによる.
○ CHITEST(観測度数の範囲,期待度数の範囲) = 0.088 > 0.05 により帰無仮説は棄却されない.
○ CHIDIST(カイ2乗,自由度8) = 0.088 > 0.05
により帰無仮説は棄却されない.
○ CHIINV(0.05,自由度8) = 15.51 > カイ2乗 13.77
により帰無仮説は棄却されない.
以上により,ポアソン分布との適合性は(消極的だが)採択される.
|