■ （各駅停車）正規分布 ※ このページは，正規分布が分からない人向けに，弱点を直しながら進めていくものです．※ あなたの解答によって，次のステップに進むか前のステップに戻るかが決まります． ※ 右図のイメージのように，間違ったときは１つ前のステップに戻ります． 計算力は実技なので，一回見ただけで身に付くことはめったにありません．行ったり来たりして「ほころび」を埋めながらゴールを目指してください． 《内容》 (1) 連続分布 (2) 標準正規分布 (3) 一般の正規分布 (4) 正規分布の記号 (5) 確率→変数 (6) まとめ |
［連続分布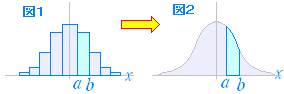］ ○ 右図１は，相対度数分布表をヒストグラムに表わしたものとする．この図において１つの階級に入る相対度数（確率）は図1において水色で示した長方形の面積に対応している． ○ 相対度数分布表の階級幅を小さくしていくと，データ数が多いとき，ヒストグラムの形は図２のような曲線（分布曲線）に近づいていく．このとき，データが a≦x≦b に入る確率は水色で示した図形の面積で表わされる． ○ 連続的な値を取り得る変数については，x=a のような正確にある値になる確率ではなくある区間 a≦x≦b に入る確率を考える． （たとえば，ある学校やある都道府県の生徒から１人選んだときに，身長が x=170.0000000000(cm) になる確率を考えても，正確に一致する人はいないので，確率は 0 になる．これは図2のグラフで，横幅 0 の区間に入る図形の面積が 0 になることからも分かる．このように，x=a のような確率は，当然 0 になることからも分かる． ） ［正規分布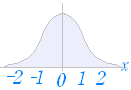］  ○ 自然現象や社会現象を観察するときによく登場するのが正規分布で，統計の基本となる分布である．正規分布の詳しい関数形を覚えても，この関数は筆算で積分計算はできない．実際に確率を求めるときは，数値積分の方法で作成されている正規分布表を使う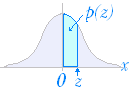．  ○ 正規分布のうち特に平均値が 0 標準偏差が 1 のものを標準正規分布という．正規分布表は標準正規分布における右図のような図形の面積（この区間に入る確率）を表にしたものである．右へ続く→ |
→続き ○ 標準正規分布のグラフに関して覚えるべきことは少しだけで，他は表を見れば分かる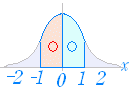．  (1) 左右対称になっている．（ 0≦x≦1 の区間の面積（確率）と，- 1≦x≦0 の区間の面積（確率）は等しいので，- 1≦x≦0 の確率を求めるには，0≦x≦1 の区間の確率を求めるとよい． 左右対称だから，右半分 0≦x に入る確率は 0.5 になる．） (2) 「帽子型」「富士山型」をしていて中央部分は高いが両側に行くほど低くなる． （ - 3≦x≦3 の範囲にほとんどの面積が含まれていて，その外側の面積は非常に小さい．） ○ 正規分布表は，教科書巻末に数表として付いていることが多い． 実際には次の値があれば十分．
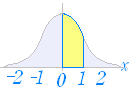 例1標準正規分布において右図の黄色で示した図形の面積を求めよ． 0.3413 …（答） 例2 標準正規分布において 0≦z≦1 となる確率 p(0≦z≦1) を求めよ． 例1の図をイメージするとよい．0.3413 …（答） |
||||||||
|
|