(参考) ■カイ2乗分布と2項分布,正規分布の関係
■カイ2乗,カイ2乗(χ2)分布とは
○ 標準正規分布に従う確率変数zの2乗がなす確率分布を自由度1のカイ2乗分布という.
χ2=z2
(2乗しているので正または0の値のみをとる.)
○ 標準正規分布に従う2個の確率変数z1,z2の2乗の和がなす確率分布を自由度2のカイ2乗分布という.
χ2=z12+z22
(2つの変数が独立に動くので,自由度1のときと比べると縦に2倍になるのでなく横に広がった形になる.)
○ 一般に標準正規分布に従うn個の独立な確率変数の2乗の和は自由度nのカイ2乗分布に従うという.
χ2=z12+z22+···+zn2
※ このように「カイ2乗分布(χ2分布)」は,もともと数学的に定義された連続関数に付けられた名前である.
これに対して「カイ2乗検定」に登場する「カイ2乗」はm×n分割表などにおいて各セル(窓枠)に入ったデータの観測度数(離散的なデータ)をもとに計算される式の値である.
以下においては,観測度数をもとに計算される「カイ2乗」をグラフや表で示される「カイ2乗分布」と照らし合わせことによって比率の検定ができる仕組みを考える.
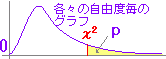
カイ2乗分布は右図2のように自由度(degree of freedom → df と略されることが多い)ごとに異なる形をした連続型の確率分布で,x≧0の区間において定義され,与えられたxの値よりも上側に来る確率は,自由度ごとに計算されて参考書の巻末表に掲載されていることが多い.(カイ2乗分布表を調べるときは自由度dfとxの値の2つ指定しなければならない.)
右図2で赤で示した自由度4(df=4)のカイ2乗分布を例として見ると,n個の確率変数が独立に動くために自由度が1のときの4倍になるのでなく(縦に伸びるのではなく)右側のすそ野の長い曲線になっており,左右非対称な山形をしている. |

図1
↓

図2
|
■2つの比率に分かれる確率・・・2項分布
1回の試行で事象Aの起こる確率がp,事象Aが起る確率がq (=1-p)であるとき,この試行をN回行ったときに事象Aがm回,事象Aがn回(合計N回)起こる確率は2項定理で求められ
NCmpmqn
となる.
■2項分布の正規分布による近似
右の表1においてNが十分大きな値のとき事象Aが起こる回数をxとすると,xは平均Np,標準偏差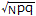 の正規分布で近似され, の正規分布で近似され,
は標準正規分布に従う.
ここで,事象Aが起こる観測度数がmとなるときのχ2を求めると
 ・・・(1)
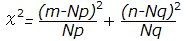 ・・・(2)
(2)式は表1における事象A,事象Aの観測度数,期待度数が各々m,Np,n,Nqであることに注意すると
の形になっている.
一般にすべてのセル(マス目)について

を加えたもの
を「カイ2乗」という.
|
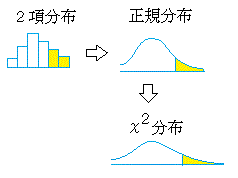
表1
| |
事象A |
事象A |
計 |
| 確率 |
p |
q |
1 |
| 観測度数 |
m |
n |
N |
さいころを100回投げて1の目が20回出た場合に,このさいころが正しく作られたものかどうか判断したい場合を考えてみると,事象Aは「さいころを投げたときに1の目が出ること」を表し,Aは「1以外の目が出ること」を表す.確率pは1/6,qは5/6,観測度数mは20,nは80,総度数Nは100になる.
正しく作られたさいころでは,1の目が100÷6≒17回程度出るはずだが確率的な偶然で実際には多少の増減はある.とすれば20回なら偶然の範囲と言えるかどうか.このように指定された比率(1/6)と実際の観測度数(100のうちの20)が等しいとみなせるかどうかを判断するのが「比率の検定」の問題である.
(*)
(2)を変形すると(1)に等しくなることが示せる.
 |
■カイ2乗の値の例
例1
右の表2において期待度数はさいころを60回投げたときに出た目の回数を集計したものとする.このさいころが「どの目も確率1/6で出るように作られているかどうか」を検定するには,
(1) はじめに観測度数の他に「どの目も確率1/6で出るように作られている」という仮定を満たす場合の期待度数を計算する・・・60×1/6=10になる.
これは基準とすべき確率分布が与えられている場合,したがって基準となる期待度数が与えられている場合になっている・・・適合性の検定の場合にはこのようにして期待度数が求められる.
(2) 次にすべてのセル(マス目)に対してχ2を求め,その和 を計算する. を計算する.
(3) 検定の内容に応じてこのχ2値をχ2表と見比べて判断する.(この例では自由度5のχ2分布表を見る.) |
表2
| 出た目 |
1 |
2 |
3 |
4 |
5 |
6 |
計 |
| 観測度数 |
13 |
12 |
8 |
6 |
11 |
10 |
60 |
| 期待度数 |
10 |
10 |
10 |
10 |
10 |
10 |
60 |
|
χ2=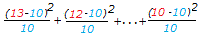
=3.40
|
例2
右の表3において観測度数は男女合計100人にある製品の好感度をアンケート調査した結果だとする.このとき,この製品の好感度は男女の性別によって違いがないかどうかを検定したいものとする.
(1) 帰無仮説として「男女の性別によって好感度には違いがない」と仮定したときの,各々のセルの期待度数の表を作る.
たとえば「男子」「よい」のセルの期待度数は,列の和27を54:46に配分したものになるべきだから27*54/100=14のように求める.(小数のままでも四捨五入して整数にしたものを使ってもよい.)
これは,性別に対して独立という仮定に基づいて,周辺度数(列の小計,行の小計)から期待度数を求めていることになる.このような独立性の検定においては,帰無仮説に基づいて観測度数から周辺和を計有して期待度数を求めることになる.
(2) 次にすべてのセル(マス目)に対してχ2を求め,その和 を計算する. を計算する.
(3) 検定の内容に応じてこのχ2値をχ2表と見比べて判断する.(この例では自由度2のχ2分布表を見る.) |
表3
| 観測度数 |
よい |
普通 |
悪い |
計 |
| 男子 |
12 |
30 |
12 |
54 |
| 女子 |
15 |
21 |
10 |
46 |
| 計 |
27 |
51 |
22 |
100 |
| |
|
|
|
|
| 期待度数 |
よい |
普通 |
悪い |
計 |
| 男子 |
14 |
27 |
11 |
54 |
| 女子 |
12 |
23 |
10 |
46 |
| 計 |
27 |
51 |
22 |
100 |
| |
|
|
|
|
| χ2 |
0.286 |
0.333 |
0.091 |
|
| |
0.750 |
0.174 |
0.000 |
|
| |
|
|
|
1.634 |
|
■自由度と確率変数の個数
2つの事象のどちらかになる回数は2項分布で与えられるが,3つの事象A,B,Cに分かれるときの自由度を考えてみる.たとえば,ある人がジャンケンでN回手を出すときに,グーをa回,チョキをb回,パーをc回出したとき,この手の出し方は均等であったかどうか調べたいものとする.
これを2段階に分けて考えて,まずAとそれ以外(BまたはC)に分かれると考えると
まずAとそれ以外に分かれる確率を求めるために確率変数z1を用い,さらにBとCに分かれる確率を求めるために確率変数z2を用いるので,A,B,Cの3つに分かれる確率を求めるためには確率変数が2つ必要になる.
このようにして,順次にn個の事象に分けるためには確率変数がn-1個必要になるから,自由度はn-1になる.
これに対して,右の表4の2×2分割表で周辺度数が与えられているときは,1つのセルの値が決まれば残りのセルの値が決まるから,2×2分割表を埋めるときの自由度は1になる.
一般に表5のようにm行×n列の分割表においてセルの期待度数を求めるときの自由度は(m-1)(n-1)になる. |
2項展開の繰り返しによって多項展開を行う考え方
(a+b)Nを展開したときのarbN-rの係数は2項定理によって求められ,NCrになる.
そこで(a+b+c)Nを展開したときのarbsctの係数を求めるには,まず(a+(b+c))Nを展開してar(b+c)N-rの係数を求めると
NCr
次に(b+c)N-rを展開するとよい.
表4
| a |
b |
a+b |
| c |
d |
c+d |
| a+c |
b+d |
N |
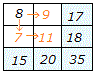 表5
表5
| |
|
|
|
|
行和1 |
| |
|
|
|
|
行和2 |
| |
|
|
|
|
行和3 |
| |
|
|
|
|
行和4 |
| |
|
|
|
|
行和5 |
| |
|
|
|
|
行和6 |
| |
|
|
|
|
行和7 |
| |
|
|
|
|
行和8 |
| |
|
|
|
|
行和9 |
| 列和1 |
列和2 |
列和3 |
列和4 |
列和5 |
合計 |
|
 (pは右片側面積)
(pは右片側面積)

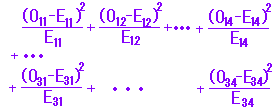





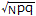 の正規分布で近似され,
の正規分布で近似され,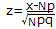
 ・・・(1)
・・・(1)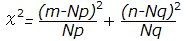 ・・・(2)
・・・(2)
 を加えたもの
を加えたもの


 (4) 右図1のように,連続分布となっている確率分布関数において,ある特定の値をとる確率というものは考えない(線の面積は0).
(4) 右図1のように,連続分布となっている確率分布関数において,ある特定の値をとる確率というものは考えない(線の面積は0).