フィッシャーの正確確率検定

→ スマホ用は別頁

=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには，次の色をクリック

◎内側の色を変えるには，次の色をクリック

◎標準文字色を変えるには，次の色をクリック

《体験・入門レベル》
== フィッシャーの正確確率検定 ==
R version 4.0.3, 4.0.4Patched
----- 最終更新年月日:2021.4.27

　この教材は，体験・入門のレベルで，30分から1時間ほどで「そこそこ分かる」ことを目指す．

フィッシャーの正確確率検定

1.　２×２クロス集計表の有意差検定

-- 表1 --
	音楽	美術	計
男子	8	2	10
女子	5	7	12
計	13	9	22

　次の表1のようなクロス集計表（架空データ）において，「男女の別」によって「芸術選択科目」に有意差があるかどうか，性別と芸術選択が独立かどうかは，通常「カイ２乗検定」によって調べることができる．
　ただし，この表の場合のように観測度数の小さいセルが含まれる場合は，「カイ２乗検定」を適用することはできず，フィッシャーの正確確率検定（直接確率計算）によって判断することになる．
　フィッシャーの正確確率検定は，理屈上は観測度数が大きな値のセルばかりの場合にも適用できるが，非常に大きな数の掛け算・割り算になり，実際に使えるかどうかはそのコンピュータ（ソフト）の性能次第になる．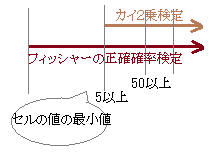

2.　フィッシャーの正確確率の考え方

2.1　片側検定

　２×２クロス集計表では，与えられた周辺和（表1では，10, 12, 22, 9, 13）を満たすセルの値は，自由度１で決まる．例えば，表1において「男子・美術」を1名とすると，男子の計が10になるためには，「男子・音楽」は9名に決まる．また，美術の計を9名とするためには，「女子・美術」は8名に決まる．最後に，「女子・音楽」は4名になる．
　このように，１つのセルの値を決めると，他のセルの値は自動的に決まる･･･このことを自由度１という．
　赤で示したセルは両方とも減るか増えるかの運命を共にする．また，青で示したセルも運命を共にする．

　カイ２乗検定の場合でも，フィッシャーの正確確率検定の場合でも，「ちょうど」このような２×２クロス集計表になる確率を求める訳ではない．この表で言えば，赤色のセルの値が「これ以上少ないことは起こり得るか」，青のセルの値が「これ以上多くなることは起こり得るか」と考える．
　つまり，次のような確率を求めて「めったに起こらないp<.05」かどうかを判断する．

-- ア --
	音楽	美術	計
男子	8	2	10
女子	5	7	12
計	13	9	22

-- イ --
	音楽	美術	計
男子	9	1	10
女子	4	8	12
計	13	9	22

-- ウ --
	音楽	美術	計
男子	10	0	10
女子	3	9	12
計	13	9	22

　美術選択者を軸に，このような場合の数を計算すると，
ア）男子10名の内2名が美術を選択する場合の数は₁₀C₂，
　女子12名の内7名が美術を選択する場合の数は₁₂C₇，
　このような選択の仕方は₁₀C₂×₁₂C₇=75×792=35,640通り
イ）男子10名の内1名が美術を選択する場合の数は₁₀C₁，
　女子12名の内8名が美術を選択する場合の数は₁₂C₈，
　このような選択の仕方は₁₀C₁×₁₂C₈=10×495=4,950通り
ウ）男子10名の内0名が美術を選択する場合の数は₁₀C₀，
　女子12名の内9名が美術を選択する場合の数は₁₂C₉，
　このような選択の仕方は₁₀C₀×₁₂C₉=1×220=220通り
　合計40,810通り
　他方，合計22名の内10名が美術を選択する場合の数は₂₂C₁₀=497,420通り
　結局，「これ以上ひどくなる確率」は 40,810÷497,420=0.08204（>.05）となり有意差は見られない．すなわち，性別による芸術選択の違いには有意差はなかった．

　以上は，片側検定の場合（すなわち，「男子の美術選択者がこんなに少ないこと」「女子の美術選択者がこんなに多い多いこと」は起こり得るかという問いに対する答）となっている．
　一般に，差異があるという場合に，逆方向の差異の確率も求めて「両側検定」とする場合もある．

2.2　両側検定

　男女の芸術選択に差異があるかどうかという場合には，前述の2.1の片側確率だけでなく，逆向きにズレている場合も含めて考えることがある．

-- エ --
	音楽	美術	計
男子	3	7	10
女子	10	2	12
計	13	9	22

-- オ --
	音楽	美術	計
男子	2	8	10
女子	11	1	12
計	13	9	22

-- カ --
	音楽	美術	計
男子	10	9	10
女子	12	0	12
計	13	9	22

　両側検定にするためには，「片側確率を単純に２倍にしても一致するとは限らない」「片側で求めたセルの数値をひっくり返せばよい訳ではない」ことに注意する．

a	b
c	d

　ここでは「ひどくズレている」ということの目印として，右のような２×２表の行列式
D=ad−bc
が，大きいかどうかで判断する．
　比較したい初めの表では，D=8×7−2×5=46であるから，逆向きの場合も含めて
|D|=|ad−bc|≧46
の場合を「ズレている」と見なすことにする．

-- キ --
	音楽	美術	計
男子	4	6	10
女子	9	3	12
計	13	9	22

　だから，右の表--キ--の場合は，|D|=|4×3−6×9|=|−42|<46は，ズレていないと見なす．
　そこで，両側検定の場合は，上記のエオカの確率を加える．
エ）　₁₀C₇×₁₂C₂=120×66=7,920通り
オ）　₁₀C₈×₁₂C₁=45×12=540通り
カ）　₁₀C₉×₁₂C₀=10×1=10通り
　合計8,470通り．確率は 8,470÷497,420=0.01703
　両側合計は，0.09907(>.05)となって，両側検定でも有意差なしとなる．

2.3　補足説明（連関係数）

-表2.3.1-
	X1	X2	小計
Y1	a	b	r1
Y2	c	d	r2
小計	c1	c2	n

　右の表2.3.1のような2×2クロス集計表に対応するクラメールの連関係数は，φファイ係数と呼ばれる．
　a+b=r1, c+d=r2, a+c=c1, b+d=c2
　a+b+c+d=nとする．
$\phi=\sqrt{\frac{\chi^2}{n}}=\frac{|ad-bc|}{\sqrt{r_1r_2c_1c_2}}$
　周辺和 $r_1,r_2,c_1,c_2$ が一定のとき，クラメールの連関係数は，行列式 $D=ad-bc$ によって決まる．

-表2.3.2-
	音楽	美術	計
男子	5	5	10
女子	6	6	12
計	11	11	22

　例えば，右の表2.3.2のように，周辺和に比例して決まるセルの値が実際の観測値と一致している場合には，男女の別と芸術選択は独立になり，この場合D＝30−30=0となる．

-表2.3.3-
	音楽	美術	計
男子	8	2	10
女子	3	9	12
計	11	11	22

　例えば，右の表2.3.3のように，男子が音楽に，女子が美術に偏っている場合は，男女別と芸術選択は独立ではなく，強い連関がある．この場合D=72−6=66となる．

-表2.3.4-
	音楽	美術	計
男子	2	8	10
女子	9	3	12
計	11	11	22

　逆に，右の表2.3.4のように，男子が美術に，女子が音楽に偏っている場合は，男女別と芸術選択は独立ではなく，強い連関がある．この場合D=6−72=−66となる．
　以上のように，２つの質的変数（男女別と芸術選択）が独立に近いほどDは0に近くなり，一方に偏っていれば|D|が大きくなる．

• 両側検定において，逆向きの偏りが同じ程度であるかどうかの目安に|D|を使うことができる．
• Rの片側検定において，alternative="g"（大きい方）とするか="l"（小さい方）とするかは，Dの大きい方を数えるか，小さい方を数えるかに対応する．

2.4　男子を軸に計算した場合

　前述の2.1，2.2では美術選択者を軸に確率を計算したが，男子（もしくは女子）を軸に計算することもできる．･･･どちらかを決めれば他方は決まる．

-- ア --
	音楽	美術	計
男子	8	2	10
女子	5	7	12
計	13	9	22

-- イ --
	音楽	美術	計
男子	9	1	10
女子	4	8	12
計	13	9	22

-- ウ --
	音楽	美術	計
男子	10	0	10
女子	3	9	12
計	13	9	22

　男子を軸に，このような場合の数を計算すると，
ア）音楽選択者13名のうち男子が8名である場合の数は₁₃C₈，
　美術選択者9名のうち男子が2名である場合の数は₉C₂，
　このような選択の仕方は₁₃C₈×₉C₂=1,287×36=46,332通り
イ）音楽選択者13名のうち男子が9名である場合の数は₁₃C₉，
　美術選択者9名のうち男子が1名である場合の数は₉C₁，
　このような選択の仕方は₁₃C₉×₉C₁=715×9=6,435通り
ウ）音楽選択者13名のうち男子が10名である場合の数は₁₃C₁₀，
　美術選択者9名のうち男子が0名である場合の数は₉C₀，
　このような選択の仕方は₁₃C₁₀×₉C₀=286×1=286通り
　合計53,053通り
　他方，合計22名の内10名が男子である場合の数は₂₂C₁₀=646,646通り
　結局，「男子が音楽ばかりになる確率」は 53,053÷646,646=0.08204（>.05）となり有意差は見られない．

　上記のエオカの場合から，逆向きの極端な場合も求めると，同様にして，両側確率が0.09907となる．

2.5　統計用フリーソフトRで計算する場合

• Rのコンソール画面で，次のように入力して行列を作る

mx<-matrix(c(8,2,5,7),2,2,byrow=T)

•　次にフィッシャー検定の関数にその行列を渡す．

fisher.test(mx)

⇒　既定値で両側検定の結果が得られる．
p-value = 0.09907(>.05)だから有意差なし
• 片側検定を行うには，alternative="greater"（または="g"）により連関係数の大きい方（Dの大きい方），alternative="less"（または="l"エル）で連関係数の小さい方（Ｄの小さい方）を指定するための引数を追加する．表アに対して表イおよび表ウは，連関係数の大きい方（Dの大きい方）になっているので"g"を指定する．

fisher.test(mx,alternative="g")

⇒　p-value = 0.08204(>.05)だから有意差なし
　なお，alternative="two.sided"もしくは省略で両側検定,

3.　演習問題

	分かり易い	分かりにくい	計
A方式	9	3	12
B方式	7	8	15
計	16	11	27

(1) ある単元の授業を新しいA方式で行った場合と，従来のB方式で行った場合に，各々事後アンケート調査を行った結果は次の表のとおりであった．
ア）　新しい教え方A方式は，従来のB方式と比べて分かり易いと言えるか．片側検定で判断してください．
イ）　これら２つの方式は，分かり易さに差異があると言えるか．両側検定で判断してください．

（解答）
　5よりも小さい値のセルがあるので，カイ２乗検定に依らずに，フィッシャーの正確確率検定で判断する．

　統計用フリーソフトRを用いる場合

-元の行列-
D=72−21=51
9	3
7	8

-含める-
D=90−12=78
10	2
6	9

-含める-
D=110−5=105
11	1
5	10

-含める-
D=132
12	0
4	11

　以上のように，元の行列に対して連関係数（または行列式）が大きい方に向かって集計するから，alternative="g"とする．

> mx<-matrix(c(9,3,7,8),2,2,byrow=T)
> fisher.test(mx,alternative="g")

⇒ p-value = 0.1368となって，片側検定で有意差は認められない．･･･ア）

　次に，両側検定を行う．

fisher.test(mx)

⇒ p-value = 0.2388となって，両側検定も有意差は認められない．･･･イ）

　Excelで行う場合（フィッシャー検定の関数がないので，次のように計算式で埋めて行く）

分かりにくい人数
	A	B	C	D	E
1	A方式	0	1	2	3
2	B方式	11	10	9	8
3	=COMBIN(12,B1)など→	1	12	66	220
4	=COMBIN(15,B2)など→	1365	3003	5005	6435
5	=B3*B4など→	1365	36036	330330	1415700

=SUM(B5:E5)→1,783,431
総数=COMBIN(27,11)→13,037,895
片側確率:1,783,431/13,037,895=0.136,788,262となって，片側検定で有意差は認められない．･･･ア）

両側確率を求めるにあたって，逆向きの組合せの範囲は

-元の行列-
D=72−21=51
9	3
7	8

-入れない-
D=30−60=−30
6	6
10	5

-入れる-
D=20−77=−57
5	7
11	4

-入れる-
D=12−96=−84
4	8
12	3

分かりにくい人数
	A	B	C	D	E	F
1	A方式	7	8	9	10	11
2	B方式	4	3	2	1	0
3	=COMBIN(12,B1)など→	792	495	220	66	12
4	=COMBIN(15,B2)など→	1365	455	105	15	1
5	=B3*B4など→	1081080	225225	23100	990	12

=SUM(B5:F5)→1,330,407
総数=COMBIN(27,11)→13,037,895
片側確率:1,330,407/13,037,895=0.102,041,549
両側確率:0.238,829,811となって，両側検定でも有意差は認められない．･･･イ）

		英語
		好き	嫌い	計
数学	好き	7	10	17
	嫌い	9	3	12
	計	16	13	29

(2) あるクラスで数学と英語の好き嫌いのアンケート調査を行った結果は次の表のとおりであった．（架空データ）
ア）数学が嫌いな生徒は英語が好きであると言えるか．片側検定で判断してください．
イ）数学と英語の好き嫌いは独立であると言えるか．両側検定で判断してください．

（解答）
　5よりも小さい値のセルがあるので，カイ２乗検定に依らずに，フィッシャーの正確確率検定で判断する．

　統計用フリーソフトRを用いる場合

-元の行列①-
D=21−90=−69
7	10
9	3

-含める②-
D=12−110=−98
6	11
10	2

-含める③-
D=5−132=−127
5	12
11	1

-含める④-
D=−146
4	13
12	0

　以上のように，元の行列に対して連関係数（または行列式D）が小さい方に向かって集計するから，alternative="l"エルとする．

> mx<-matrix(c(7,10,9,3),2,2,byrow=T)
> fisher.test(mx,alternative="l")

⇒ p-value = 0.07621となって，片側検定で有意差は認められない．･･･ア）
　次に，両側検定を行う．

fisher.test(mx)

⇒ p-value = 0.1297となって，両側検定でも有意差は認められない．･･･イ）

　Excelで行う場合（フィッシャーの正確確率検定の関数がないので，次のように計算式で埋めて行く）
①：₁₆C₉×₁₃C₃=11,440×286=3,271,840
②：₁₆C₁₀×₁₃C₂=8,008×78=624,624
③：₁₆C₁₁×₁₃C₁=4,368×13=56,784
④：₁₆C₁₂×₁₃C₀=1,820×1=1,820
片側小計3,955,068
総計:₂₉C₁₂=51,895,935
片側確率:3,955,068÷51,895,935=0.076211518（>.05）となって，片側検定で有意差は認められない．･･･ア）

両側確率を求めるにあたって，逆向きの組合せの範囲は

-元の行列①-
D=21−90=−69
7	10
9	3

-入れない-
D=77−30=47
11	6
5	7

-入れる⑤-
D=96−20=76
12	5
4	8

-入れる⑥-
D=117−12=105
13	4
3	9

-入れる⑦-
D=140−6=−134
14	3
2	10

-入れる⑧-
D=165−2=163
15	2
1	11

-入れる⑨-
D=192
16	1
0	12

　同様にして，⑤～⑨までを加えると，2,778,321
片側確率:2,778,321/51,895,935=0.053,536,39
両側確率:0.129,747,908となって，両側検定でも有意差は認められない．･･･イ）

...（PC版）メニューに戻る