→ スマホ用は別頁
|
=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには,次の色をクリック
《体験・入門レベル》
== Rによるグラフの表示 == R version 4.0.3, 4.0.4Patched ----- 最終更新年月日:2021.4.04
この教材は,体験・入門のレベルで,30分から1時間ほどで「そこそこ分かる」ことを目指す.
関数のグラフ
具体例からスタート
(1) Rのコンソール画面で,次のように入力すると,y=sinxのグラフが表示される.
curve(sin) 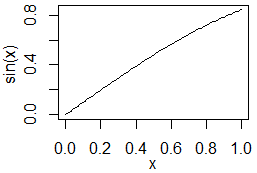
• Rに組み込まれている関数は,curve( )の中に関数名を書く[sinなど]かxを変数として関数を書けば[sin(x)など],その関数の概形が表示される.
• この例のように,区間を省略すれば0.0≦x≦1.0の区間で関数が表示される. |
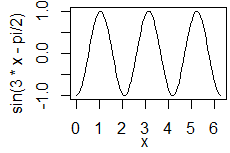
(2) 第2引数,第3引数として数値を記入すれば,各々グラフを表示する区間の下端と上端を表す.
curve(sin(2*x), 0, pi) 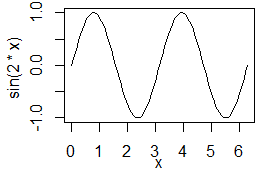
• 正弦関数を省略せずに書くときはsin(x)と書く.sin2xはsin(2*x)と言う形で定数との積で書く
from= , to= という名前付きタグによって区間の下端と上端を表す場合は,第2第3引数以外の場所に記入してもよい.
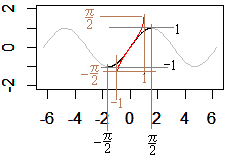
• 円周率は記号定数piで表す.この他,自然対数の底[ネイピア数]を表す記号定数はないので,指数関数を使ってexp(1)とすればよい. curve(cos(x/2),to=pi,from=-pi)  |
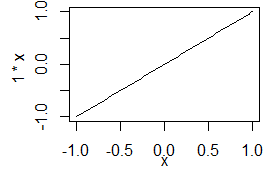

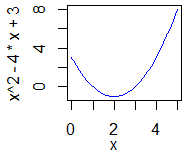
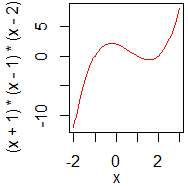

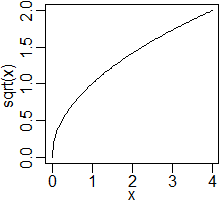
 (ⅰ)
(ⅰ) 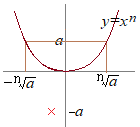 (ⅱ)
(ⅱ) 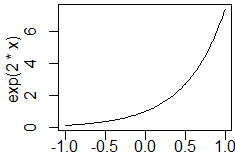
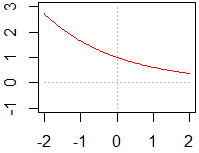
 • 単に sin と書けば,sin(x)の省略形と解される.
• 単に sin と書けば,sin(x)の省略形と解される.
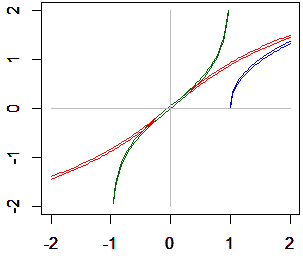
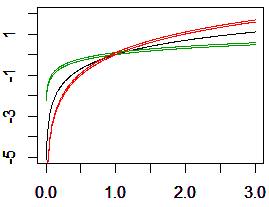
 • 黒色は
• 黒色は • 赤は
• 赤は