|
=== �z�F��ύX�������ꍇ ===
���O���̐F��ς���ɂ́C���̐F���N���b�N
== ���v�p�t���[�\�t�gR �̊�{���� == R version 4.0.3 (2020-10-10) ----- �ŏI�X�V�N����:2021.1.16 1.�@�Z�p���Z
(1)�@�R���s���[�^�ɐ��l�Ƃ��ĔF������邽�߂ɂ́C���p�����i�P�o�C�g�̃A�X�L�[�����j�����ŏ����Ȃ���Ȃ�Ȃ��D�S�p�����ŏ����ꂽ�����́C�i�Q�o�C�g�����̂P, �Q�Ȃǁj���l�Ƃ��ĔF������Ȃ��D
(2)�@���l�Ɖ��Z�q�̊ԂɁu���p�X�y�[�X�v�u�S�p�X�y�[�X�v�������Ă����������D
�@�ނ���C�ꑱ���̕ϐ����Ȃǂƕ���킵���Ȃ��悤�ɁC���₷���C�ԈႢ�ɂ��������ɂ́C���l��ϐ��ȂǂƉ��Z�q�̊Ԃɂ́u���p�X�y�[�X���P�����v�Ƃ����������ɑ����闬�V�������߁D
(3)�@C�����Javascript�ȂǂƂ͈قȂ�C�C���N�������g�C�f�N�������g���Z�q�i++, −−�j�͎g��Ȃ��D
�@�Q�ȏ�̉��Z�q�𑱂��ėp�����ꍇ�C3++4��3+(+4)�C3+−4��3+(−4)�C3−−4��3−(−4)�C3+−+4��3+(−(+4))�C3−+−4��3−(+(−4))�Ƃ����悤�ɁC�擪��+�܂���−�����Z�q�Ɖ��߂��C���͕����Ɖ��߂����悤���D�������C����킵���̂ł��̂悤�������́C�����߂��Ȃ��D �@�擪�̂݉��Z�q�Ŏc��͕����Ƃ����Ӗ��ł́C3+*4�̓G���[�C3*+4��3*4�ɓ������C3+/4�̓G���[�C3/+4��3/4�ɓ������C3*/4�̓G���[�ɂȂ�D �@�������C�ݏ�i�ׂ���j�Ƃ��āC3**4��3^4�ɓ��������̂Ƃ݂Ȃ����D3**(1/2)��3�̐��̂Q�捪�C���Ȃ킿��3=1.732051�i7���܂ł̏����j�ɂȂ�D |
1.1�@�����Z
�y��1.1.1�z > 1+2 [1] 3 �y��1.1.2�z > 3+(-4)+0.7 [1] -0.3 1.2�@�����Z
�y��1.2.1�z > 2-5 [1] -3 �y��1.2.2�z > 2-(-5)-0.7 [1] 6.3 1.3�@�|���Z
�y��1.3.1�z > 3*4 [1] 12 �y��1.3.2�z > 3 * (-4) * 0.5 [1] -6 1.4�@����Z
�y��1.4.1�z > 14/4 [1] 3.5 �y��1.4.2�z > 14/3 [1] 4.666667
�@����Z�̉��Z / ���g���ƁC����ꂽ�琮���ŁC�L�������ɂȂ�Ƃ��͗L���̌��܂ŁC���������ɂȂ�Ƃ��͏������Ԃ����i�\�����7���܂ŁC�����������I�ɕێ����Ă��錅���͂����Ƒ傫���j�D
�y��1.4.3�z > 4/(3*5) [1] 0.2666667 �y��1.4.4�z > 4/3/5 [1] 0.2666667
�@�Q�̐��Ŋ���i�Q��Ƃ��́j�y��1.4.3�z�̏����������y��1.4.4�z�̏��������悭��������D
1.5�@�ݏ�
�@R�Łua��b��v�Ƃ����ׂ���i�ݏ�j��\���ɂ�a^b���g���Da**b���\�D�y��1.5.1�z > 3^4 [1] 81 �y��1.5.2�z > 3**(1/2) [1] 1.732051 |
 a=bq+r
a=bq+r 14 %/% 3 → 4 … ����́Cfloor(14/3)�ɓ�����
14 %/% 3 → 4 … ����́Cfloor(14/3)�ɓ����� �A�@���̐������̐��̏ꍇ
�A�@���̐������̐��̏ꍇ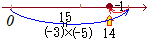 �B�@���̐������̐��̏ꍇ
�B�@���̐������̐��̏ꍇ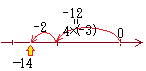 �C�@���̐������̐��̏ꍇ
�C�@���̐������̐��̏ꍇ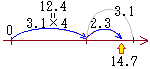 14.7 %/% 3.1 → 4 … ����́Cfloor(14.7/3.1)�ɓ�����
14.7 %/% 3.1 → 4 … ����́Cfloor(14.7/3.1)�ɓ�����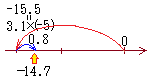 �A�@���̐������̐��̏ꍇ
�A�@���̐������̐��̏ꍇ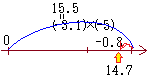 �B�@���̐������̐��̏ꍇ
�B�@���̐������̐��̏ꍇ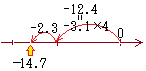 �C�@���̐������̐��̏ꍇ
�C�@���̐������̐��̏ꍇ