○(ア) 原理(2変数で説明)
複数の変数に座標変換を行って,不偏分散が最大となるような新変数(主成分)を作る.
資料間の差異が一番はっきり分かる変数(主成分)を作る
= 不偏分散が最大となる新変数を求める
=(2変数の場合) X = ax +
by とおいてXの不偏分散が最大となる係数a,bを定める.
ただし,係数a,bを大きくすれば不偏分散は幾らでも大きくなるのでベクトル(a,b)の大きさが1という条件を付ける.
これは図のように回転させて新変数X の不偏分散が最大となるように変形することに対応している.
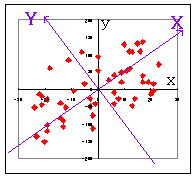 元の説明変数の不偏分散の和を全体の情報量と考えると新しく導入した変数(主成分)X の不偏分散の大きさがこの主成分によって説明できる情報量となる.
元の説明変数の不偏分散の和を全体の情報量と考えると新しく導入した変数(主成分)X の不偏分散の大きさがこの主成分によって説明できる情報量となる.
2変数の場合,元の変数x,yの不偏分散をSx,Sy とし,主成分X,Yの不偏分散をSX,SY とするとき,回転移動である限り,SX +SY = Sx+ Sy = S(全体の情報量)が成り立つ.
主成分X の情報の割合SX/(Sx+ Sy) を主成分X の寄与率という.また,寄与率を順次加えていったものを累積寄与率という.(累積寄与率の総和は1となる.)
累積寄与率が7〜8割程度=大半の情報量となるまで主成分の個数を増やしていく. |
3変数の場合
| |
項目1
x1 |
項目2
x2 |
項目3
x3 |
|
第1主成分 |
第2主成分 |
| 学生1 |
85 |
91 |
55 |
|
128.2371 |
-26.2092 |
| 学生2 |
65 |
52 |
75 |
|
90.1834 |
-15.0506 |
| 学生3 |
51 |
72 |
76 |
|
102.0853 |
4.3433 |
| ・・・ |
・・・ |
・・・ |
・・・ |
|
・・・ |
・・・ |
| 学生24 |
81 |
52 |
35 |
|
87.7293 |
-42.3946 |
| 学生25 |
48 |
65 |
41 |
|
86.6469 |
-6.9407 |
上のようなデータがあるときに,項目1〜項目3のデータを幾つかの指標にまとめて資料(学生1〜学生25)の差異を明らかにする.
そのために z = ax1+ bx2+cx3 で定義される変数zを導入しその(不偏)分散が最大となるように定数a,b,cを定める.
このように定めた変数zを第1主成分とする.
第1主成分だけで元の変数項目1〜3の(不偏)分散のほとんどが説明しつくされることは少なく,第2主成分,・・・との組合せで各資料の傾向を表現することになる.その際,第1主成分と第2主成分は無相関となるようにする.
第1主成分を係数ベクトル(a,b,c)で表わし,第2主成分を係数ベクトル(d,e,f)で表わすとき,これらを無相関とするには,これら2つのベクトルが垂直になるようにする.
第3主成分を導入するときは第1主成分とも第2主成分とも垂直となるようにする.
※ 係数ベクトル(a,b,c),(d,e,f)は,各々逆向きでも条件を満たすので,求め方(以下の解説では初期値の与え方)によっては,逆向き(-a,-b,-c),(-d,-e,-f)の組合わせも同じ結果が出る. |
○(イ) 分散共分散行列を用いる方法(2変数で説明)
上記のように分散が最大となるものは,数学的には分散共分散行列の固有値,固有ベクトルに対応することが知られている.
すなわちX = ax + by のときX の分散 S が最大
⇔ Sは分散共分散行列の固有値のとき最大となる
(a,b)はその固有値に対する固有ベクトル(大きさ1)となる.
最も大きな固有値に対応するX を第1主成分とする.
次に大きい固有値に対応するものを第2主成分とする.
この形の実対称行列では,一般に,説明変数(この例ではx,y)の個数だけ正の固有値が存在し,各々の固有ベクトルは互いに垂直となることが知られている.
※ ただし,Excelの「ツール」→「分析ツール」→「共分散」で求められる分散共分散行列は母集団を扱っている場合の値となるので,今の場合,標本の大きさをnとするとき
n/(n-1)を掛けた不偏分散に直して使う. |
3変数の場合
分散共分散行列は「ツール」→「分析ツール」→「共分散」で求められる.(下三角行列となるので対称行列となるように上三角の部分を埋めるとよい.・・・コピー→作業用の範囲に行と列を入れ替えて貼り付け.対角成分を削除して,「形式を選択して貼り付け」→加算・値の貼り付け など)
| 分散 |
項目1 |
項目2 |
項目3 |
| 項目1 |
323.16 |
31.82 |
-4.73 |
| 項目2 |
31.82 |
362.87 |
33.99 |
| 項目3 |
-4.73 |
33.99 |
265.69 |

標本の大きさ(個数)をnとするとき
各成分に n/(n-1) を掛けたもの
| 不偏分散:A |
項目1 |
項目2 |
項目3 |
| 項目1 |
336.63 |
33.15 |
-4.93 |
| 項目2 |
33.15 |
377.99 |
35.40 |
| 項目3 |
-4.93 |
35.40 |
276.76 |
この表の場合,元の説明変数による不偏分散の総和(情報量)は336.63+377.99+276.76=991.38
固有値λ1=403.12となるので,第1主成分の寄与率は,403.12/991.38=0.407
固有値λ2=325.85となるので,第2主成分の寄与率は,325.85/991.38=0.329 累積寄与率は0.736となる.
(元の情報量の73.6%の説明ができるので第2主成分まで採用すればよい.) |
○(ウ) 変数を基準化(規格化,標準化)する方法
各説明変数の単位が異なるときや値のスケールが違うときは各説明変数を基準化(規格化,標準化)してから主成分分析を行うのがよい.
すなわち各説明変数を (説明変数 - 平均)/不偏標準偏差 に変換したもので分析するとよい.この場合,基準化(規格化,標準化)された変数の平均値は0,分散は1となる.
以後の処理方法は(ア)の場合と同じ
(第2主成分以降の計算において係数ベクトルの垂直条件が必要)
|
3変数の場合
| 基準化データ |
項目1 |
項目2 |
項目3 |
| 学生1 |
1.947 |
2.039 |
0.452 |
| 学生2 |
0.857 |
0.033 |
1.654 |
| 学生3 |
0.094 |
1.062 |
1.714 |
| 学生4 |
0.748 |
0.856 |
-0.450 |
| 学生5 |
1.729 |
0.033 |
-0.750 |
| 学生6 |
-0.070 |
0.702 |
-0.390 |
のようなデータからスタートする.
分散の総和は説明変数の個数nになり,求めた主成分の分散が1以下になれば情報量の少ない主成分として打ち切ればよい. |
○(エ) 相関係数行列を用いる方法
相関係数はその定義において変数を基準化(規格化,標準化)したものとなっているので,元の変数から相関係数行列を求めた場合,結果は(ウ)の場合と同じになる.
この相関係数行列の固有値,固有ベクトルを求めればよい.
各固有値はn ≧λ1≧λ2≧・・・≧λn≧ 0
λ1+λ2+・・・+λn = n
を満たす.
各主成分の寄与率(全体の分散のうちその主成分で説明できる割合)はλk/n で,累積寄与率は (λ1+λ2+・・・+λk)/ n となる.
固有値が1より小の主成分は元の変数よりも情報量が少ないので固有値が1以上の主成分までを使うのを目安とする(カイザー基準). |
3変数の場合
相関係数行列は「ツール」→「分析ツール」→「相関」で求められる.(下三角行列となるので対称行列となるように上三角の部分を埋めるとよい.・・・コピー→作業用の範囲に行と列を入れ替えて貼り付け.対角成分を削除して,「形式を選択して貼り付け」→加算・値の貼り付け など)
| 相関係数 |
項目1 |
項目2 |
項目3 |
| 項目1 |
1.0000 |
0.0929 |
-0.0162 |
| 項目2 |
0.0929 |
1.0000 |
0.1095 |
| 項目3 |
-0.0162 |
0.1095 |
1.0000 |
相関係数行列では,各主成分の分散が固有値になり,全体の分散は説明変数の個数となる.(対角成分の和=1+1+1+・・・=n)
そこで相関係数行列の固有値を大きいものから順に求めればよい.
|