�y���3.1�z
�@���̕\�́C����X�ʼnʕ������ꂽ���ԑ�(0�`23)���L�^�������̂��Ƃ��܂��D�i�ˋ�f�[�^�j
-�\3.2-
| �݂��� | ��� | ���� |
| 7 | 18 | 15 |
| 11 | 20 | 3 |
| 5 | 21 | 5 |
| 19 | 7 |
| 10 | |
�@���̕\����C�ʕ��̎�ނƔ��ꂽ���ԑт̑��֔���C��L�̂܂Ƃ�(1)�`(4)�̕��@�ŋ��߂Ă��������D
�@���ɁC(4)�̕��@�ł́CP-�l��p���āC�L�ӂȌQ�ԕϓ�������Ƃ����邩�ǂ��������f���Ă��������D
(1) ���̂悤�ɕ\��������E�ցC�ォ�牺�֏�������ōs���C�Ō�ɑ��֔�����߂�D�i�Ȃ��CExcel��͏����������������C���̉�ʏ�͏�����1�ʂ܂ŕ\�������j
| ���ԑ� | �Q���� | ��2�� | �S�̕� | ��2�� |
| �݂��� | 7 | −4 | 16 | −5.6 | 31.2 |
| �݂��� | 11 | 0 | 0 | −1.6 | 2.5 |
| �݂��� | 15 | 4 | 16 | 2.4 | 5.8 |
| ��� | 18 | 0.4 | 0.2 | 5.4 | 29.3 |
| ��� | 20 | 2.4 | 5.8 | 7.4 | 55.0 |
| ��� | 21 | 3.4 | 11.6 | 8.4 | 70.8 |
| ��� | 19 | 1.4 | 2.0 | 6.4 | 41.2 |
| ��� | 10 | −7.6 | 57.8 | −2.6 | 6.7 |
| ���� | 15 | 7.5 | 56.3 | 2.4 | 5.8 |
| ���� | 3 | −4.5 | 20.3 | −9.6 | 91.8 |
| ���� | 5 | −2.5 | 6.3 | −7.6 | 57.5 |
| ���� | 7 | −0.5 | 0.3 | −5.6 | 31.2 |
| �݂��� | 11 | �a | 192.2 | �a | 428.9 |
| ����� | 17.6 | | | ���֔� | 0.55 |
| �������� | 7.5 | | | | |
| �S�̕��� | 12.6 | | | | |
(2)
�݂���=11, �����=17.6, ��������=7.5, �S�̕���=12.6������
(�Q�ԕϓ�)=(11−12.6)�~3+(17.6−12.6)�~5+(7.5−12.6)�~4=236.7
(�S�ϓ�)=428.9
(���֔�)=236.7/428.9=0.55
(3)
�݂���̕��U=10.7��3�{���݂���̌Q���ϓ�=32.0
��̕��U=15.4��5�{�������S�̌Q���ϓ�=77.2
�����̕��U=20.8��4�{�������̌Q���ϓ�=83.0
�S�̂̕��U=35.7��12�{���S�ϓ�=428.9
(���֔�)=1−(32.0+77.2+83.0)/428.9=0.55
(4)
-�\3.2-�̌`����C(Excel��)�f�[�^���f�[�^���́����U���́F�ꌳ�z�u�ɐi��
�o���i�݂���`�����j���܂߂āC�݂���C�����̋��܂߂ē��͔͈͂��w�肷��D
| �T�v | |
| �O���[�v | �W�{�� | ���v | ���� | ���U |
| �݂��� | 3 | 33 | 11 | 16 |
| ��� | 5 | 88 | 17.6 | 19.3 |
| ���� | 4 | 30 | 7.5 | 27.7 |
| ���U���͕\ |
| �ϓ��v�� | �ϓ� | ���R�x | ���U | �ϑ����ꂽ
���U�� | P-�l | F ���E�l |
| �O���[�v�� | 236.7 | 2 | 118.36 | 5.54 | 0.03 | 4.26 |
| �O���[�v�� | 192.2 | 9 | 21.36 | | | |
| | | | | | |
| ���v | 428.9 | 11 | | | | |
�\�ɂ��C(���֔�)=236.7/428.9=0.55
P-�l��0.03<0.05������L�Ӑ���5%�ŌQ�ԕϓ���������
�����適

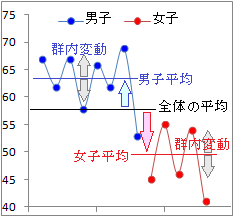
 ���u�������ւ�����v�Ɋ܂߂�̂͂��������Ƃ������܂��D
���u�������ւ�����v�Ɋ܂߂�̂͂��������Ƃ������܂��D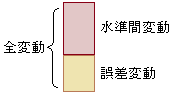 �@��������́C(�����ԕϓ�)��(�덷�ϓ�)���v�Z����F�l�������́C���̃��[�g�̂��l��p���čs���D
�@��������́C(�����ԕϓ�)��(�덷�ϓ�)���v�Z����F�l�������́C���̃��[�g�̂��l��p���čs���D