.

■t分布　･･･　母集団が正規分布で，母標準偏差が未知，標本数が少ないとき (概ねn が30未満)の推定と検定

■要約■
　小さい標本 n （概ね30未満）から母集団の値を推定するときｔ分布を用いる．
○　母集団が正規分布，標本の大きさ n ＜30のとき，次の値 t を用いて，自由度 n-1 のｔ分布で考える．
　（標本平均：m，母平均：μ，母標準偏差：σ，標本(単純)標準偏差：s，標本(不偏)標準偏差：u　とする）
　
　(1)　標本(不偏)標準偏差：uで計算するとき
　(2) 標本（単純）標準偏差 s で計算するとき

○　ｔ分布のグラフは正規分布のグラフと似ているが，各自由度ごとにグラフが異なるので，正規分布と同じように１つの表として示すことはできない．（コンピュータで行うときはこの制限はない．）

両すその面積の和がpになるようなｔの値
　 ｐの値
自由度 : n-1 0.1 0.05 0.01
1 6.314 12.706 63.656
2 2.920 4.303 9.925
3 2.353 3.182 5.841
4 2.132 2.776 4.604
･･･ ･･･ ･･･ ･･･

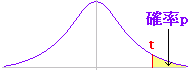
　(1)　よく使われる確率に絞って，自由度-確率に対応するｔの値が求められるようになっている．
　(2)　ｔ分布のグラフは左右対称となっている．
　(3)　片側検定に用いるには，２倍のpの値に対応するｔを求めればよい．

※　ｔ分布の表として，上記のようにA「pを両すその面積で表示するもの」の他，B「ｐを片側の面積で表示するもの」，C「-∞からの累積（1-Bの面積）」などがある．何を表わした表か確認してから使うことが重要．

例　n=5(自由度n-1=4)のとき，両すその和が0.05（5%）となるtの値は2.776
[ 詳しいｔ分布表は右下欄 ]
 ※　Student のt分布
　Studentは，「学生の成績の分布？」とは関係ない．この分布を研究した統計学者のペンネーム
　正規分布や二項分布のように，実際にｔ分布に従う事象があるのでなく，標本の性質（統計量）から母集団の性質（母数）を推定するための正規分布の補正表というべきか．
○　母標準偏差σが未知のとき，nが大きければ標本標準偏差sで代用できるが，ｎが小さくなるほど誤差がひどくなるので，標本の値から母標準偏差σを推定するには標本(不偏)標準偏差 u を用いる．（これは単なる経験則でなく，理論の裏付けあり．）

○　標本 x1, x2, ･･･ , xnの（単純な）標準偏差
に対して，母標準偏差を推定するときは，分母を n-1 に替えたもの
を使う．u2 は不偏分散と呼ばれる．

　u2 はどの書物でも「不偏分散」と書かれているが， u は「母標準偏差の不偏推定値」「不偏分散から求めた標準偏差」「標本に基づいて予測した標準偏差」などと表記は多様．気楽に"不偏偏差"といいたいところだが，手持ちの書物にはこの用語はない．専門家にとっては不偏推定量を使うのが当然なので，uのことを標本標準偏差，標準偏差と呼ぶ場合もあるが，このページでは初学者に区別が分かりやすいように，ｓ：標本(単純)標準偏差，ｕ：標本（不偏）標準偏差，σ：母標準偏差とする．

○　母標準偏差：σ，標本(不偏)標準偏差：ｕ，標本(単純)標準偏差：ｓの関係
・標本(不偏)標準偏差：u は母標準偏差：σの近似値として使える：u≒σ
・定義から だから =
・ｎ＞30のときは，σ, u, s はほぼ等しい．
※　自由度
例　2次元のxy平面全体ではｘもｙも自由に決められるので，自由度は2
　しかし，xy平面上で x+ y = 1 という条件を満たすx，yの組では，xを決めるとｙが決まるから，自由に決められる変数は１個
　自由度は 2 - 1=1

例　3次元空間ではx，y，zが自由に決められるから，３次元空間全体の自由度は３
　しかし， x + y + z = 5 という条件を満たすx，y，zの組では，x，yを決めるとzが決まるから，自由に決められる変数の数は2個
　自由度は 3 - 1 = 2
　
このように，条件式を１つ追加すると，自由度は１個減る．
○　平均値が m となる変数の組　 x1 ， x2 ， … ， xn は，次の方程式を満たす．
m = ( x1 + x2 + … + xn )

変数が n個で方程式が1個だから自由度は n-1
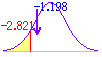
○　正規分布を用いる推定や検定と比べると，正規分布表の代わりにｔ分布表を用いることと，自由度（標本の大きさ-1)を考えることが異なるが，考え方は正規分布を用いた推定や検定と同様

例1［推定］
　誤差が正規分布をなすと考えられる製品から標本10個を無作為抽出したところ，重さの標本平均は148.5(g)，標本（単純）標準偏差は3(g)であった．この製品の母平均の信頼度95%の信頼区間を求めよ．
（解答） n＜30なのでｔ分布による
= (148.5-μ)/1
　自由度9のｔ分布でp=0.05のとなるのはt=2.262
-2.262≦148.5-μ≦2.262より
146.2≦μ≦150.8
例2［両側検定］
　ある錠剤は１粒あたり平均250.0mgのビタミンＣを含むものと定められている．錠剤の標本20個を無作為抽出したとき，ビタミンＣの含有量は１粒当り平均249.5mg，標本（単純）標準偏差0.5mgであった．この標本を取り出した母集団の錠剤は規格を来しているか．有意水準1%で検定せよ．
（解答）n＜30なのでｔ分布による
= (249.5-250.0)/0.1147=-4.359
　自由度19のｔ分布でp=0.01のとなるのはt=2.861
-4.359＜-2.861
棄却域に入るから，規格を満たしていない．
例3［片側検定］
　標本の大きさ n = 12，標本平均 m = 305，標本（不偏）標準偏差 u = 5，有意水準 α = 0.01　のとき，帰無仮説H0：μ = 300，対立仮説：μ＞300 の検定をせよ．
（解答）n＜30なのでｔ分布による
= (305-300)/1.443=3.465
　自由度11のｔ分布で（両側で）p=0.02となるのはt=2.718
2.718＜3.465
棄却域に入るから，帰無仮説は棄却され，対立仮説が採択される．
※［ t分布表 ］ 　
両すその面積の和が p になるような t の値
　 pの値
自由度n-1 0.1 0.05 0.02 0.01
1 6.314 12.706 31.821 63.656
2 2.920 4.303 6.965 9.925
3 2.353 3.182 4.541 5.841
4 2.132 2.776 3.747 4.604
5 2.015 2.571 3.365 4.032
6 1.943 2.447 3.143 3.707
7 1.895 2.365 2.998 3.499
8 1.860 2.306 2.896 3.355
9 1.833 2.262 2.821 3.250
10 1.812 2.228 2.764 3.169
11 1.796 2.201 2.718 3.106
12 1.782 2.179 2.681 3.055
13 1.771 2.160 2.650 3.012
14 1.761 2.145 2.624 2.977
15 1.753 2.131 2.602 2.947
16 1.746 2.120 2.583 2.921
17 1.740 2.110 2.567 2.898
18 1.734 2.101 2.552 2.878
19 1.729 2.093 2.539 2.861
20 1.725 2.086 2.528 2.845
21 1.721 2.080 2.518 2.831
22 1.717 2.074 2.508 2.819
23 1.714 2.069 2.500 2.807
24 1.711 2.064 2.492 2.797
25 1.708 2.060 2.485 2.787
26 1.706 2.056 2.479 2.779
27 1.703 2.052 2.473 2.771
28 1.701 2.048 2.467 2.763
29 1.699 2.045 2.462 2.756
30 1.697 2.042 2.457 2.750
■例と答■
(1)［推定］
　ある会社の製品であるゴルフボールから12個抽出して重さを測定したところ，標本平均45.8(g)，標本（単純）標準偏差1(g)であった．この製品の母平均の信頼度95%の信頼区間を求めよ．

［※架空の問題です．45.93(g)以下という規則があるそうです．］

 （解答）標本の大きさ（個数）が12＜30なのでｔ分布を用いる．
= (45.8 - μ)/(1/3.317) = (45.8 - μ)/0.3014
ｔ分布で自由度11，ｐ=0.05となるｔの値は2.201
-2.201≦(45.8 - μ)/0.3014≦2.201より
45.13≦μ≦46.46
(2)［両側検定］
　ある小麦粉は，１袋の内容量1000(g)として販売されている．この小麦粉15袋を無作為抽出して測定したところ，標本平均1002(g)，標本（単純）標準偏差2(g)であった．この袋詰めは正しく行われているかどうか有意水準5%で検定せよ．		 （解答）標本の大きさ（個数）が15＜30なのでｔ検定とする．
H0：μ = 1000， H1：μ ≠ 1000　で両側検定を行う．
= (1002-1000)/(2/3.74) = 2/0.535 = 3.738
ｔ分布で自由度14，ｐ=0.05となるｔの値は2.145
2.145＜3.738　だから帰無仮説棄却．
袋詰めは正しく行われていない．
(3)［片側検定］
　母集団が正規分布をしていると考えられるとき，標本の大きさ n = 10，標本平均 m = 49.8，標本(単純)標準偏差 ｓ = 0.5，有意水準 α = 0.01　のとき，帰無仮説H0：μ = 50.0，対立仮説：μ＜50.0 の検定をせよ． 		（解答）標本の大きさ（個数）が10＜30なのでｔ検定とする．
H0：μ = 50.0， H1：μ ＜ 50.0　で片側検定を行う．
= (49.8-50.0)/(0.5/3) = -0.2/0.167 = -1.198
ｔ分布で自由度9，ｐ=0.02となるｔの値は2.821
-2.821＜-1.198　だから帰無仮説は棄却されない．
■Excelを用いた計算■
利用できる主な関数名，利用方法 概要，例
=TINV(確率, 自由度)

　値を求めたいセルに直接 =TINV(0.05, 10) のように書き込む

　または，メニューから「挿入」→「関数」→関数の分類「統計」→関数名「TINV」→確率の欄に0.05など有意水準（危険率）または有意水準の小数が記入されたセル名を記入→自由度の欄に標本の大きさ-1の自由度を記入→ＯＫ

※　引数（パラメータ）を有意水準，自由度の順に書き込む点に注意		 ○　メニューでは「スチューデントｔ-分布の逆関数を返します」と表示されるが，この関数で
自由度n-1，有意水準p → t値 が求まる．
例
　 A B C D E F G
1 　 　 　 確率p
2 　 　 自由度 0.1 0.05 0.02 0.01
3 　 　 9 1.833 2.262 2.821 3.250
4 2.201 　 10 1.812 2.228 2.764 3.169
5 　 　 11 1.796 2.201 2.718 3.106
6 　 　 12 1.782 2.179 2.681 3.055
　セルA4に=TINV(0.05,11) と記入すれば，上のような値が返される．
　セルD3に=TINV(D$2, $C3) と記入し，この式をD3からG6までコピー･貼付すると，上のようなｔ分布表ができる．

※　この関数は，確率，自由度からｔ値を求めるものなので，信頼区間の推定にも，検定にも使える．
=TDIST(X, 自由度, 尾部)
Xのところにｔ値を記入
自由度には標本数-1を記入
尾部には，両側の確率を求めるときは2を，片側の確率を求めるときは１を記入		 ○　指定されたX（ｔ値）の外側にあるｔ分布の確率を返す．
　　　ｔ値（X），自由度，片側か両側か→確率p が求まる．
尾部が2のとき→
尾部が1のとき→
例
　 A
1 0.050
　セルA1に =TDIST(2.226,10,2) と記入すると，t = 2.226, n-1 = 10, 両側 のときの確率p が0.05と返される．

※　この関数は，ｔ値，自由度，両側か片側かを指定して確率を求めるものなので検定に使える．
(単純)標準偏差の計算　=STDEVP(範囲)
　範囲内に空白や文字列データがあってそれらを0とみなして計算したいとき（個数ｎに含めるとき）は　STDEVPA(範囲)を用い，それらを個数に数えたくないときは=STDEVP(範囲)を用いる．

(不偏)標準偏差の計算　=STDEV(範囲)
　範囲内に空白や文字列データがあってそれらを0とみなして計算したいとき（個数ｎに含めるとき）は　STDEVA(範囲)を用い，それらを個数に数えたくないときは=STDEVA(範囲)を用いる．
　なお，蛇足ながらこの関数を利用せずにΣ(xk - m)2 から定義に従って計算するときは，平均（期待値）mは標本の大きさｎで割ることに注意

正の平方根の計算　=SQRT(セルまたは値)
　 Ａ B C
1 3.7 　 　
2 4.1 　 　
3 4.8 　 　
4 5.5 　 　
5 5.6 　 　
6 5.8 　 　
7 6.1 　 　
8 6.7 　 1.194
9 7.8 　 1.267
例
　セルC8に　=STDEVP(A1:A9)　と記入すればC8にA1〜A9までの値の（単純）標準偏差1.194が返される．
（「母集団の標準偏差を求める」とは，単純に個数ｎで割った標準偏差を求めるということ）
　セルC9に　=STDEV(A1:A9)　と記入すればC9にA1〜A9までの値の（不偏）標準偏差1.267が返される．
（「標本に基づいて予測した標準偏差を求める」とは，ｎ-1で割った不偏推定値の標準偏差を求めるということ）
=C8/SQRT(8)， =C9/SQRT(9)　はいずれも0.422 となる．
■例と答■
(1)［推定］
　得点が正規分布に従うと考えられる多数の答案の中から9枚を無作為抽出して採点した結果は次のとおりであった．
　　38, 44, 70, 53, 50, 34, 51, 49, 58
　この試験で母平均の信頼度95%の信頼区間を求めよ．		 （解答）
標本の得点をA1からA9に入力し，
=AVERAGE(A1:A9)　で標本平均 m=49.667 を求めておく．
=STDEVP(A1:A9)　で標本（単純）標準偏差s=10.055 が得られる．
=TINV(0.05, 8) を求めると，t=2.306　となるので
49.667±2.306×10.055/SQRT(8)　より
41.4≦μ≦57.9となる

※　=STDEV(A1:A9)　で標本（不偏）標準偏差u=10.665を求めて，49.667±2.306×10.665/SQRT(9)　としても同様

※　メニューから「ツール」→「分析ツール」→「基本統計量」→入力範囲：A1:A9，平均の信頼区間の出力：95%
として出力される値 8.198 は上の赤字部分（平均からの幅）
.
(2)［両側検定］
　ある食品の内容量(g)について標本12個を無作為抽出して検査したところ，次の結果が得られた．
48.2, 54.7, 51.0, 49.3, 46.9, 46.8, 49.6, 46.9, 47.0, 50.9, 50.2, 45.9
　この製品は母平均50.0(g)という条件を満たしているといえるか．危険率5%で検定せよ．		 （解答）標本の大きさ（個数）が12＜30なのでｔ検定とする．
H0：μ = 50.0， H1：μ ≠ 50.0　で両側検定を行う．

標本の値をA1からA12に入力し，
=AVERAGE(A1:A12)　で標本平均 m=48.95 を求めておく．
=STDEV(A1:A12)　で標本（不偏）標準偏差u=2.52 が得られる．
=TINV(0.05, 11) を求めると，t=2.20　
|m-50.0|/(u/SQRT(12)) = 1.44＜2.20だから
帰無仮説は棄却されない．

※　=TDIST(1.44, 11, 2)を求めると0.17となりp＞0.05だから帰無仮説は棄却されない．
(3)［片側検定］
　ある会社では通勤距離3.0km以下の社員には通勤手当は支給されず，3.0kmを超える社員についてはその距離に応じた通勤手当が支給される．自宅から会社までの通勤距離を15回測定したところ，次の結果が得られた．
3.02, 3.16, 2.95, 2.99, 3.32,
3.21, 2.86, 2.85, 3.08, 2.93,
3.00, 2.92, 3.22, 3.10, 2.98　
　この社員には通勤手当を支給すべきかどうか有意水準5%で検定せよ． 		（解答）標本の大きさ（個数）が15＜30なのでｔ検定とする．
3.0kmを超えるかどうかが問題だから片側検定とする．
H0：μ = 3.0， H1：μ ＞ 3.0　で片側検定を行う．

標本の値をA1からA15に入力し，
=AVERAGE(A1:A15)　で標本平均 m=3.039 を求めておく．
=STDEV(A1:A15)　で標本（不偏）標準偏差u=0.139 が得られる．
=TINV(0.10, 14) を求めると，t=1.76　
|3.039-3.0|/(u/SQRT(15)) = 1.096＜1.76だから
帰無仮説は棄却されない．

※　=TDIST(1.096, 14, 1)を求めると0.146となりp＞0.05だから帰無仮説は棄却されない．支給すべきだとは言えない．
確率統計のメニューに戻る 高校数学のメニューに戻る
■［個別の頁からの質問に対する回答］[t分布について／16.12.24］
t分布が、よく理解できていないので、いきなりt分布の応用問題の解き方を教えていただいても、理解できた感じがしません。　お手数ですが、正規分布やｔ分布関数の導入の仕方を、分かりやすく解説頂けないでしょうか？
＝＞［作者］：連絡ありがとう．メニューから正規分布，ｔ分布と順に読んでください