← PC用は別頁
|
*** 科目 *** 数Ⅰ・A数Ⅱ・B数Ⅲ高卒・大学初年度 *** 単元 *** 数と式不等式二次関数二次不等式三角比三角比と図形集合・命題・証明順列・組合せ確率整数の性質 ※高校数学Aの「整数の性質…2進法,N進法」について,このサイトには次の教材があります.
この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は,他の頁を見てください. が現在地です. ↓最大公約数,最小公倍数,互除法 ↓1次不定方程式の整数解 ↓センター試験.整数問題 ↓ペル方程式 ↓2進法,16進法,n進法⇔10進法 ↓2進数の演算 ↓N進法 ↓N進数の演算 ↓N進法の小数 ↓試験問題(素数,剰余類) ↓3n+1問題(コラッツ予想)  ↓フェルマー予想,オイラー予想 連続整数の積 |
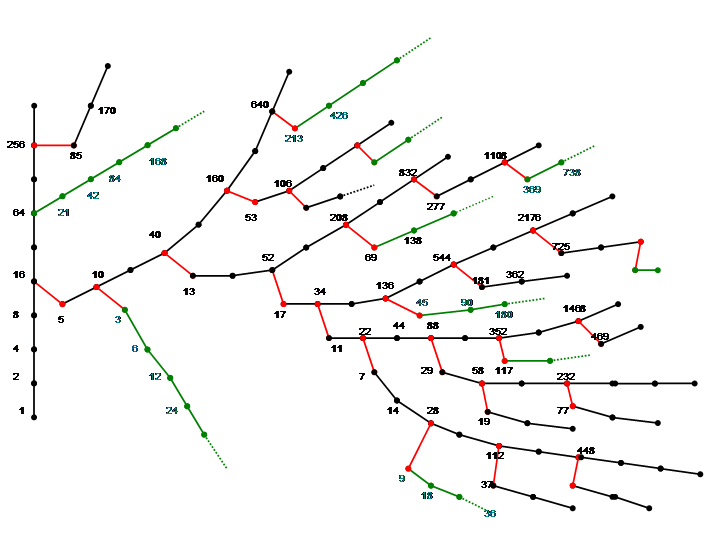
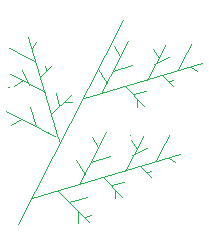 (C) ツリー1はシダ類植物の葉のように,相似図形になっている.
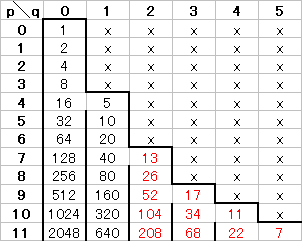
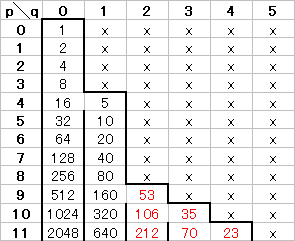
(C) ツリー1はシダ類植物の葉のように,相似図形になっている.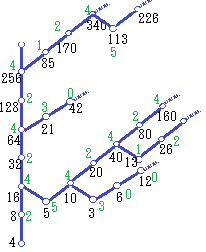 右の図は,ツリーの一部を示したもので,黒字は元の数,緑字は6で割ったときの余りです.
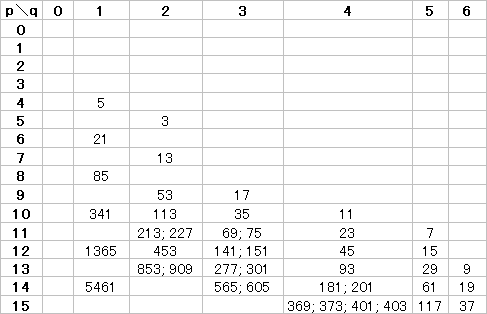
右の図は,ツリーの一部を示したもので,黒字は元の数,緑字は6で割ったときの余りです.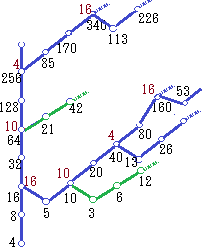 右の図で茶色字は18で割ったときの余りです.
[1]
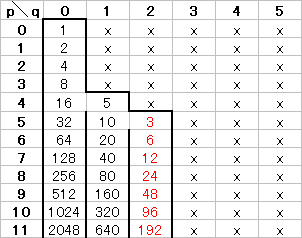
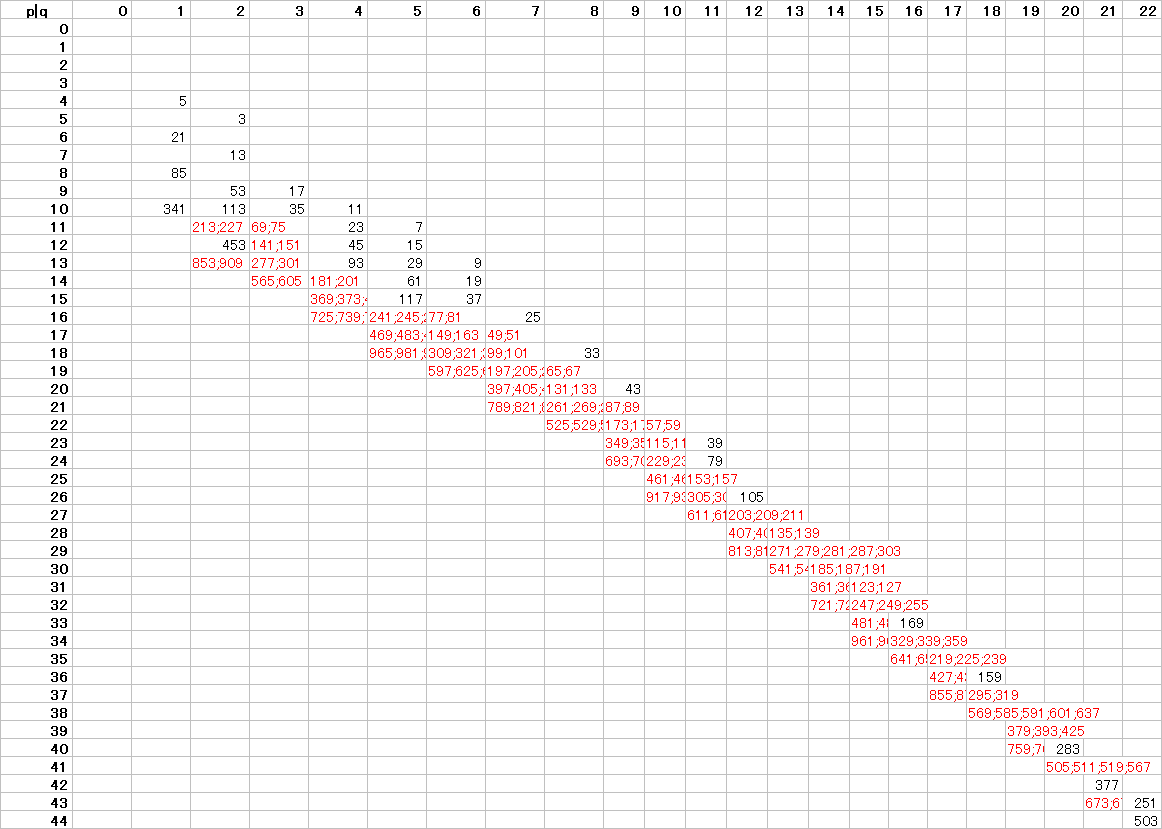
右の図で茶色字は18で割ったときの余りです.
[1]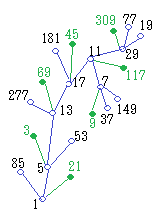
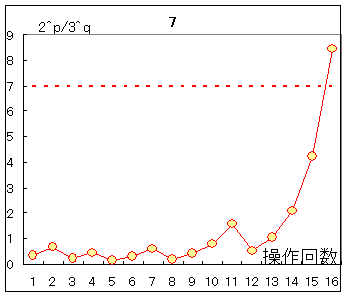
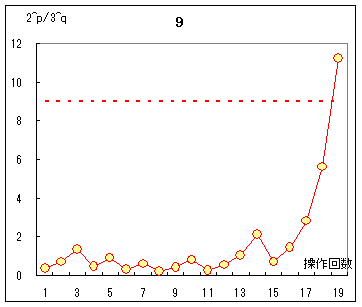
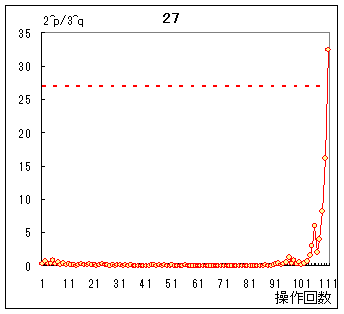
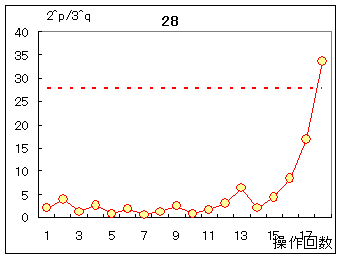
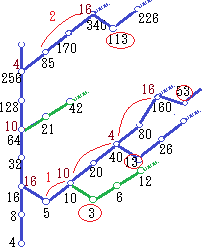 右図のように,5から逆順に見て奇数番目の項から3が分岐している場合には,上記のように2n−1乗になりますが,85から逆順に見て偶数番目の項から113が分岐しているような場合には,2n乗になります
右図のように,5から逆順に見て奇数番目の項から3が分岐している場合には,上記のように2n−1乗になりますが,85から逆順に見て偶数番目の項から113が分岐しているような場合には,2n乗になります
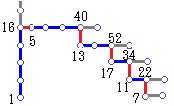 (G) 興味ある性質
(G) 興味ある性質