|
=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには,次の色をクリック
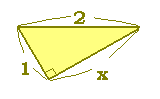
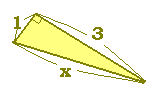
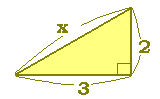
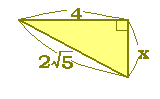
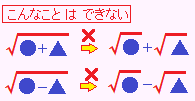
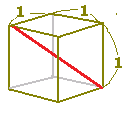
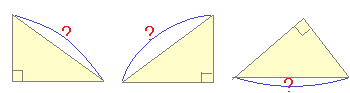
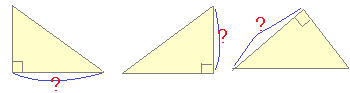
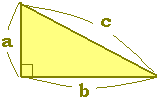
《解説》 ■次のような直角三角形の3辺の長さについては, a2+b2=c2
が成り立ちます.(これを三平方の定理といいます.)
 |
現在地と前後の項目 *** 基本 ***/三平方の定理1/三平方の定理2/三平方の定理(徹底復習)/*** 距離 ***/2点間の距離1/2点間の距離2/2点間の距離3/震源地/*** 逆の問題 ***/三平方の定理の逆/*** 融合問題 ***/融合問題/問題以上,答以下/展開図形/回転図形1/回転図形2/円と三平方の定理/*** よく出る応用 ***/三角形2個の問題1/三角形2個の問題2/三角形2個の問題3/特別な形の三角形1/特別な形の三角形2/三辺→高さ/*** 空間図形 ***/空間図形と三平方の定理1/空間図形と三平方の定理2/立体の体積,表面積/立体の体積(入試問題)/立体の表面積.展開図(入試問題)/ 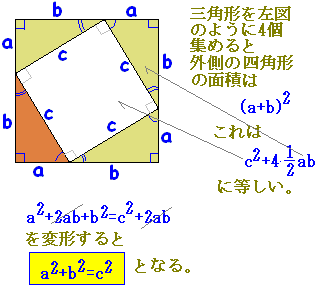 |