|
■複素数の計算 ■虚数単位iの導入 根号を用いて2次方程式を解くには、x2=a ⇒ x=±という変形を行います。 これによりx2=−1を解くと、x=±のように根号の中が負である数が登場します。 同様にして、x2=−2 ⇒ x=± x2=−3 ⇒ x=± となりますが、「負の数のルート」を表す記号を1つずつ作らなくても1つだけi=と定めると、他の負の数のルートはすべてこのiで表すことができます。
【虚数単位iの定義】
さらに、x2−2x+5=0すなわち(x−1)2=−4のような2次方程式についてもx2=−1の1つの解を虚数単位といい、iで表します。 すなわち i= …(1) i2=−1 …(2) x−1=± x−1=±2i x=1±2i 一般に2次方程式を解くと、 (x−p)2=−q ⇒ x−p=± x=p± の形の数が登場します。(p , qは実数) そこでa+bi (a , bは実数)の形の数を考えれば、すべての2次方程式の解を表すことができます。このa+bi (a , bは実数)の形の数を複素数といい,aを実部、bを虚部といいいます。 |
■虚数単位i=を定義すると、負の数のルートはすべてこの虚数単位で表すことができます。
(1) −=−i
(2) ===i (3) ===i (4) ===2i (5) ===i (6) ===i
※ 負の数のルートについて,次のようなものは必ずしも等しいとはいえません.
○ 正しく変形するためには,「負の数のルートが登場したら,そのたびに虚数単位iで表すようにします.」
×←××→
※ 次の変形規則が自由に使えるのは,a>0, b>0の場合であり,それ以外の場合は必ずしも成り立つとは限りません.(解説)
•
• だから, • だから, • だから,
•
• だから, • だから, • だから,
×=i×i=i2 =−
= になります. |
|
【問題1】
(右の選択肢から選んでください.)次の式を計算してください.負の数のルートが登場するときは,虚数単位iを使って表してください. (1)
負の数のルートを取り除いて代わりに正の数のルートと虚数単位iを付けます.
=i ※負の数のルート=iは,x2=−5の2つある解のうちの一方を表しており,両方を表している訳ではありません.もう一方は−=−iになります. |
HELP 5i −5i i −i ±i |
|
(2)
負の数のルートを取り除いて代わりに正の数のルートと虚数単位iを付けます.
=i 正の数のルートについては,中学校以来の計算規則に従って計算します. i=3i |
HELP 9i −9i 3i −3i |
|
(3)
負の数のルートを取り除いて代わりに正の数のルートと虚数単位iを付けます.
=i 正の数のルートについては,中学校以来の計算規則に従って計算します. i=i=2i |
HELP 12i −12i ±2i 2i |
|
(4)
−
負の数のルートの部分を虚数単位iで表し,他の部分はそのままにします.
−=−i 正の数のルートについては,中学校以来の計算規則に従って計算します. −i=−i=−3i |
HELP 18i −18i 3i −3i ±3i |
|
(5)
負の数のルートを「各々」虚数単位iで表します.(根号の中を先に計算してはいけません.)
=(i)(i) 正の数のルートについては,中学校以来の計算規則に従って計算します. (2i)(3i)=6i2 虚数単位iの計算規則に従って虚数単位i2を−1に変えます. 6i2=−6 |
HELP 6i −6 ±6i 216i −216i |
|
【複素数の定義】
a+bi (a , bは実数)の形の数を複素数といい、aを実部、bを虚部という。(2つの要素から成り立っている数・・・複素数) 複素数のうちで、特にb=0のものを実数という。 例 5+0iすなわち5は実数 これに対してb≠0のものを虚数という。 例 5−3iは虚数 複素数のうちで、特にa=0のものを純虚数という。 例 0+3iすなわち3iは純虚数
【複素数の計算規則】
○ iを含む式は,最終的にa+bi (a, bは実数)の形になるように変形します.(1)虚数単位iを含んだ式の和差積商は,普通の文字式におけるaやxと同じように,係数をまとめて簡単にしたり,展開,約分など行うことができます.
2a+3a=5aと同様に2i+3i=5iとできます.
(2+x)(3+x)=6+5x+x2と同様に(2+i)(3+i)=6+5i+i2とできます. (x−2)2=x2−4x+4と同様に(i−2)2=i2−4i+4とできます. それでは,虚数単位の定義はどうなったのかと心配になりますが,普通の文字とは次の点が異なります. (2)虚数単位i2が登場したら−1に書き換えます.(登場するたびに書き換えてもよく,まとめて書き換えてもよい.)
(1+i)2=1+2i+i2=1+2i+(−1)=2i
i3=i2i=−i i4=i2i2=(−1)×(−1)=1 上で求めたi3=−iの結果を使ってi4=i3i=−i×i=−(−1)=1としてもよい.(どの段階で−1に書き換えても同じになります.)
例
(1+2i)+(3+4i)=4+6i
○ iを分母に含む式は,無理数の分母の有理化と同様の変形(共役複素数を掛ける)により,分母を実数にします.(1+2i)−(5+7i)=−4−5i (1+2i)(1−3i)=1−i−6i2=1−i+6=7−i
分母がa+bi ⇒ 分母分子にa−biを掛ける.
例
分母がa−bi ⇒ 分母分子にa+biを掛ける.
===
と同様にして ===−i (※iで割ることが符号を変えることと同じ結果になり,奇妙に見えますが, i2=−1だから=−i が成り立ちます.)
====−1+
と同様にして === (i2=−1に注意)
※一般には,分母を2乗にしても実数にはできません.分母を実数にするためには,分母a+biの虚部の符号が逆のa−bi(共役複素数)を掛けなければなりません.
=== ←× ==== ←○ |
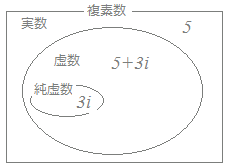 一番広い範囲のa+biの形で表される数が複素数です. ※正確に言えば のような分数は,複素数としてa+bi (a, bは実数)の形で「実部と虚部に分けて表す」と +i(a=, b=ということ) になりますが,「いつでも分けられる」ということが分かるので,最終形として は許容されます. ※これに対して, や のような式をそのまま放置しておいてはいけません.これらの式では,実部と虚部が分かりません. 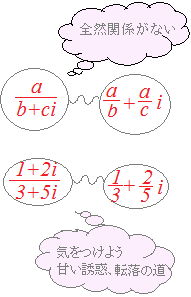 |
|
【問題2】
(右の選択肢から選んでください.)次の式を簡単にしてください. (1) (1−3i)−(2−5i)
(1−3i)−(2−5i)=1−3i−2+5i=−1+2i
|
HELP −3+2i −1+2i −1−8i −3−8i 13+11i −13−11i |
|
(2)
(2+3i)(1−i)
普通の文字式と同様に展開します.
(2+3i)(1−i)=2−2i+3i−3i2 i2を−1に書き換えます. 2−2i+3i−3i2=2−2i+3i+3=5+i |
HELP 3+2i −1+5i 5+i 5−5i |
|
(3)
(1−i)2
普通の文字式と同様に展開します.
(1−i)2=1−2i+i2 i2を−1に書き換えます. 1−2i+i2=1−2i−1=−2i |
HELP 0 2i −2i 2−2i |
|
(4)
i3+i4+i5+i6
i2ずつ束にします.
i2×i+i2×i2+i2×i2×i+i2×i2×i2 i2を−1に書き換えます. (−1)×i+(−1)×(−1)+(−1)×(−1)×i+(−1)×(−1)×(−1)=−i+1+i−1=0 |
HELP 0 2 4 2i 4i |
|
(5)
分母分子にiを掛けます.
== i2を−1に書き換えます. =−2−3i |
HELP 1 2+3i 3+2i −2+3i −2−3i |
|
(6)
分母分子に1−iを掛けます.
== i2を−1に書き換えます. =3+i |
HELP 2+4i 3+i 6+2i 6−2i |
|
【複素数の相等】
(解説)a, b, c, dが実数のとき ○ 2つの複素数が等しいのは,実部も虚部も等しいときに限る. a+bi=c+di ⇔ a=cかつb=d…(1) ○ 特に, a+bi=0 ⇔ a=0かつb=0…(2) (※複素数の等式1つは,実部と虚部に分けた1組の連立方程式と同じ値打があるということです.) (1) 実部だけが等しくても,2つの複素数が等しいとは言いません. 5+3i≠5+4i 虚部だけが等しくても,2つの複素数が等しいとは言いません. 4+3i≠5+5+3i 実部が少ない分を虚部が埋めわせることはできません. 3+5i≠5+3i (2) 0+0iのとき,単に0と書きます. ※(1)から(2),(2)から(1)のどちらも導けますので,どちらでやってもかまいません. |
【例】 x, yが実数のとき, x+3i=4+yiならばx=4かつy=3
(1)を使って,両辺の実部と虚部をそれぞれ比較すれば得られます.
ただし,(1)から(2),(2)から(1)のどちらも導けますので,(2)でやってもかまいません. たとえば, x+3i=4+yi ⇔(x−4)+(3−y)i=0 ⇔x−4=0かつ3−y=0 ⇔x=4かつy=3 とすれば(2)で考えていることになります. ※x, yが実数という条件がなければ,この問題は解けません. 例えば 1) x=−3i, y=4iのとき,(−3i)+3i=0, 4+4i2=0 となって,x+3i=4+yiが成り立ちます. 2) x=4−3i, y=0のとき,(4−3i)+3i=4+0i となって,x+3i=4+yiが成り立ちます. *) 要するに,x, yが実数という条件がなければ,x+3i=4+yiを満たす複素数x, yは幾らでもあります. |
|
【問題3】
(右の選択肢から選んでください.)次の等式を満たす実数x, yを求めてください. (1) x+4i=5+yi
実部の比較からx=5,虚部の比較からy=4となります.
(なお,yi=4iという答案をよく見かけますが,iを取り除いた形で答えるようにしましょう.) |
HELP x=5, y=4 x=4, y=5 x=5, y=4i x=4i, y=5 |
|
(2)
3x+yi+(6−i)=0
(3x+6)+(y−1)i=0⇔3x+6=0かつy−1=0
⇔x=−2かつy=1 |
HELP x=2, y=1 x=2, y=−1 x=−2, y=1 x=−2, y=−1 |
|
(3)
(−2+i)x+(3−i)y=−7+3i
(−2x+3y)+(x−y)i=−7+3i
⇔
−2x+3y=−7…(A)
x−y=3…(B)
−2x+3y=−7 +)2x−2y=6 y=−1 (B)に代入:x=2 |
HELP x=2, y=1 x=2, y=−1 x=−2, y=1 x=−2, y=−1 |
|
(4)
(x+yi)(2−3i)=−7−9i
2x−3xi+2yi−3yi2=−7−9i
(2x+3y)+(−3x+2y)i=−7−9i ⇔
2x+3y=−7…(A)
−3x+2y=−9…(B)
4x+6y=−14 −)−9x+6y=−27 13x=13 x=1 (A)に代入:y=−3 |
HELP x=1, y=3 x=1, y=−3 x=−1, y=3 x=−1, y=−3 |
|
【問題4】 (実係数方程式の虚数解)
(右の選択肢から選んでください.)x=2−iが2次方程式x2+ax+b=0の解となるように実数a, bの値を定めてください.
慣れていないと難しい問題に見えますが,x=2−iが2次方程式x2+ax+b=0の解だから,代入すると成り立つはずです.
(2−i)2+a(2−i)+b=0 ここでa, bが実数だから,複素数の相等を使えば,係数比較の問題となります. 4−4i+i2+2a−ai+b=0 (3+2a+b)+(−a−4)i=0 ⇔
3+2a+b=0…(A)
−a−4=0…(B)
a=−4 (A)に代入:b=5 |
HELP a=4, b=5 a=4, b=−5 a=−4, b=5 a=−4, b=−5 |
|
【問題5】 (実係数方程式の虚数解)
(右の選択肢から選んでください.)x=1+iが3次方程式x3+ax+b=0の解となるように実数a, bの値を定めてください.
x=1+iが3次方程式x3+ax+b=0の解だから,代入すると成り立つはずです.
(1+i)3+a(1+i)+b=0 ここでa, bが実数だから,複素数の相等を使えば,係数比較の問題となります. ⇔1+3i+3i2+i3+a+ai+b=0 ⇔1+3i−3−i+a+ai+b=0 ⇔(−2+a+b)+(2+a)i=0 ⇔
−2+a+b=0…(A)
2+a=0…(B)
a=−2 (A)に代入:b=4 |
HELP a=2, b=4 a=2, b=−4 a=−2, b=4 a=−2, b=−4 |
|
【問題6】 (複素係数方程式の実数解)
(右の選択肢から選んでください.)2次方程式x2+(a+2i)x−(4+8i)=0が実数解をもつように実数aの値を定めてください.
※実係数の2次方程式ax2+bx+c=0 (a≠0)が実数解を持つ条件は,判別式D=b2−4acの符号によって調べることができますが,複素係数方程式が実数解を持つ条件は判別式の符号では調べられません.
実数a, xに対して,x2+(a+2i)x−(4+8i)=0が成り立つのだから,複素数の相等を使えば,係数比較の問題となります.
そもそも,a, b, cが実数であれば,2次方程式の解の公式から x=…(*) から虚数解が出てくる原因は,根号内b2−4acが負の数になる場合しかありません.だから,D=b2−4acの符号を調べれば,実数解をもつか虚数解をもつかを判別できたわけです. しかし,係数a, b, cが複素数であれば,上記の式(*)において,分母の2aや分子の−bはそれ単独で虚数となる可能性があります.このような訳で,複素係数方程式が実数解をもつ条件は判別式では調べられません. x2+ax+2xi−4−8i=0 ⇔(x2+ax−4)+(2x−8)i=0 ⇔
x2+ax−4=0…(A)
2x−8=0…(B)
x=4 (A)に代入:a=−3 |
HELP a=2 a=−2 a=3 a=−3 a=4 a=−4 |