|
【ド・モアブルの定理】
【例】nを整数とするとき (cosθ+i sinθ)n=cos(nθ)+i sin(nθ) …(1)  (1)(cos+i sin)3=cos+i sin (2)(cos+i sin)4=cosπ+i sinπ (定理の解説) 正式には,次の公式を数学的帰納法で示すのがよいが,ここでは具体的に順を追って示してみる. ア) n>0のとき 次の公式を使う.
(cosα+i sinα)(cosβ+i sinβ)=cos(α+β)+i sin(α+β)
n=2のとき
(cosθ+i sinθ)2=(cosθ+i sinθ)(cosθ+i sinθ)
n=3のとき=cos2θ+i sin2θ だから,(cosθ+i sinθ)2=cos2θ+i sin2θが成り立つ.
(cosθ+i sinθ)3=(cosθ+i sinθ)2(cosθ+i sinθ)
………=(cos2θ+i sin2θ)(cosθ+i sinθ) =cos(2θ+θ)+i sin(2θ+θ) =cos3θ+i sin3θ だから,(cosθ+i sinθ)3=cos3θ+i sin3θが成り立つ. n=kのとき
(cosθ+i sinθ)k=(cosθ+i sinθ)k−1(cosθ+i sinθ)
=(cos(k−1)θ+i sin(k−1)θ)(cosθ+i sinθ) =cosnθ+i sinnθ だから,(cosθ+i sinθ)k=cos kθ+i sin kθが成り立つ. |
イ)n=0のとき
(cosθ+i sinθ)0=1
ウ)n<0のときcos0+i sin0=1 だから,(cosθ+i sinθ)0=cos 0θ+i sin 0θが成り立つ. 次の公式を使う.
=cos(α−β)+i sin(α−β)
n=−1のとき
(cosθ+i sinθ)−1==
n=−2のとき=cos(0−θ)+i sin(0−θ)=cos(−θ)+i sin(−θ) だから,(cosθ+i sinθ)−1=cos(−θ)+i sin(−θ)が成り立つ.
(cosθ+i sinθ)−2==
n=−kのとき=cos(0−2θ)+i sin(0−2θ)=cos(−2θ)+i sin(−2θ) だから,(cosθ+i sinθ)−2=cos(−2θ)+i sin(−2θ)が成り立つ.
(cosθ+i sinθ)−k==
=cos(0−kθ)+i sin(0−kθ)=cos(−kθ)+i sin(−kθ) だから,(cosθ+i sinθ)−k=cos(−kθ)+i sin(−kθ)が成り立つ. 高校では扱わないが,次のオイラーの公式を使えば,ド・モアブルの定理は簡単に導かれる.
【オイラーの公式】eiθ=cosθ+i sinθ
→ (cosθ+i sinθ)n=(eiθ)n=einθ=cosnθ+i sinnθ |
|
【問題1】 次の複素数を求めてください.(正しい選択肢をクリック)
ド・モアブルの定理にあてはめます.
(cos+i sin )3=cos(3×)+i sin(3×) =cos+i sin=i…(答)
ド・モアブルの定理にあてはめます.
(cos+i sin )4=cos(4×)+i sin(4×) =cos2π+i sin2π=1…(答)
ド・モアブルの定理にあてはめます.
(cos+i sin )−2=cos(−2×)+i sin(−2×) =cos(− )+i sin(− )=−i…(答)
ド・モアブルの定理にあてはめます.
(cos+i sin )−4=cos(−4×)+i sin(−4×) =cos(− )+i sin(− )=…(答) |
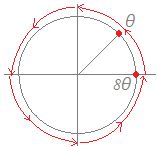 極形式で表してド・モアブルの定理が適用できるようにします. 極形式で表してド・モアブルの定理が適用できるようにします.(1+i)8 ={(cos+i sin )}8 =16(cos+i sin)8 =16(cos2π+i sin2π)=16…(答) 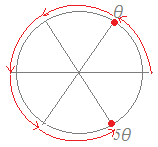 極形式で表してド・モアブルの定理が適用できるようにします. 極形式で表してド・モアブルの定理が適用できるようにします.()5 =(cos+i sin )5 =cos+i sin =…(答) |
|
【1のn乗根】
(解説)○ nを正の整数とするとき,1のn乗根は cos(×k)+i sin(×k) (k=0, 1, 2, ..., n−1) …(2) ○ 1の虚数n乗根のうちの1つを ω=cos()+i sin() で表すとき,上記の1のn乗根は 1, ω, ω2, ω3,.., ωn−1 …(3) に等しい. (2)← 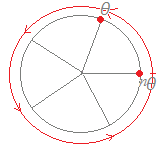 ○n=5として1の5乗根を例にとって解説する.
○n=5として1の5乗根を例にとって解説する.方程式x5=1の解は5個あるが,これらを1の5乗根という. 1) (cos+i sin)5 =cos2π+i sin2π=1 だから x=cos+i sin は,方程式x5=1の1つの解となる.(右図のように偏角の5倍がちょうど2πとなって1に等しくなる.) 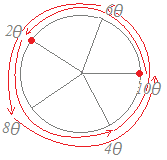 2) (cos+i sin)5
2) (cos+i sin)5=cos4π+i sin4π=1 だから x=cos+i sin は,方程式x5=1の1つの解となる.(右図のように偏角の5倍がちょうど4πとなって1に等しくなる.この場合は,円を2周して1に一致する.) 3) 同様にして x=cos(×3)+i sin(×3), cos(×4)+i sin(×4) も各々方程式x5=1の解となる.(3周もしくは4周して1に一致する.) 4) これら4個の他に,x=1すなわち x=cos+i sin もx5=1の解となる. 以上により, cos(×k)+i sin(×k) (k=0, 1, 2, ..., 4) の5つの複素数はx5=1の解となる. (3)← ω=cos+i sin で表すと ω2=cos(×2)+i sin(×2) ω3=cos(×3)+i sin(×3) ω4=cos(×4)+i sin(×4) となるから,1, ω, ω2, ω3,.., ω4はx5=1の解となる. |
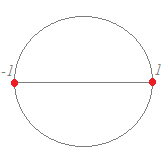 【例】
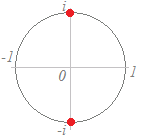
【例】○ x2=1の解は, cos()+i sin()=1 cos()+i sin()=−1 の2個になる. このとき,2つの解x=1とx=−1とは,複素数平面上での単位円を2等分する位置にある. 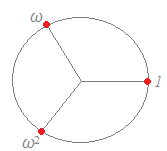 ○ x3=1の解は,
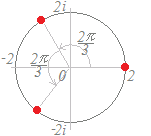
○ x3=1の解は,cos()+i sin()=1 ω=cos()+i sin() ω2=cos()+i sin() の3個になる. このとき,3つの解 1 ω=cos()+i sin() ω2=cos()+i sin() は,複素数平面上での単位円を3等分する位置に並ぶ.  ○ x4=1の解は,
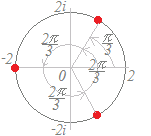
○ x4=1の解は,cos()+i sin()=1 i=cos()+i sin()=i i2=cos()+i sin()=−1 i3=cos()+i sin()=−i の4個になる. このとき,4つの解 1 i=cos()+i sin() i2=cos()+i sin() i3=cos()+i sin() は,複素数平面上での単位円を4等分する位置に並ぶ. |
|
【aのn乗根】
(解説)○ aの極形式をa=r(cosθ+i sinθ) (r>0) とするとき,xn=a (nは正の整数)の解は { cos()+i sin() }(k=0, 1, 2, ..., n−1) { cos()+i sin() }をn乗すると 絶対値はrになり, 偏角はθ+2kπになるから, r(cos(θ+2kπ)+i sin(θ+2kπ))=r(cosθ+i sinθ)=aが成り立つ.
{ cos()+i sin() }
を { cos(+)+i sin(+) } と分けてみればわかるように, 絶対値はrのn乗根になり, 偏角はa=r(cosθ+i sinθ)のn分の1から始まり円周をn等分する点となる.(右図参照)
【例1】
方程式x2=−1の解を求めるには, 1) 右辺を極形式に直す. cosπ+i sinπ 2) 1つの解は cos+i sin=i 3) 他の点を円周を2等分した角に置く. cos+i sin=−i 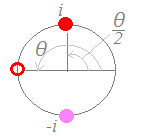
【例2】
方程式x3=iの解を求めるには, 1) 右辺を極形式に直す. cos+i sin 2) 1つの解は cos+i sin= 3) 他の点を円周を3等分した角に置く. cos(+)+i sin(+)= cos(+)+i sin(+)=−i  |
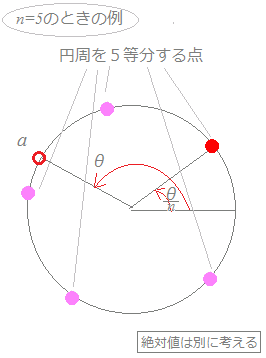
【例3】
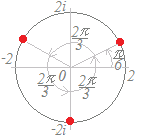
方程式x3=2(−1+i)の解を求めるには, 1) 右辺を極形式に直す. 2( cos+i sin ) 2) 1つの解は {cos+i sin }=1+i 3) 他の点を円周を3等分した角に置く. {cos(+)+i sin(+) }
=(cos+i sin ) {cos(+)+i sin(+ )}
=(cos+i sin ) 後ろの2つは三角関数の加法定理を用いれば根号などで表すこともできる.  |
|
【問題2】
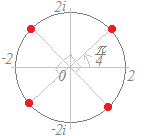
次の方程式の解を複素数平面上で図示したものを右から選んでください. ○はじめに問題を1つ選び,続いて図を選んでください. ○不正解となった問題をやり直すときは,問題を選び直すことからはじめてください. HELP
右辺のiを極形式で表すと
cos+i sin
となるので,x2=iの1つの解は
HELP
cos+i sin この解を原点の周りにπだけ回転するともう1つの解が得られる.
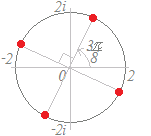
右辺の−iを極形式で表すと
cos+i sin
となるので,x2=−iの1つの解は
HELP
cos+i sin この解を原点の周りにπだけ回転するともう1つの解が得られる.
右辺の−8を極形式で表すと
8(cosπ+i sinπ)
となるので,x3=−8の1つの解は
HELP
2(cos+i sin) この解を原点の周りにずつ回転すると他の2つの解が得られる.
右辺の8iを極形式で表すと
8(cos+i sin)
となるので,x3=8iの1つの解は
HELP
2(cos+i sin) この解を原点の周りにずつ回転すると他の2つの解が得られる.
右辺の−16を極形式で表すと
16(cosπ+i sinπ)
となるので,x4=−16の1つの解は
HELP
2(cos+i sin) この解を原点の周りにずつ回転すると他の3つの解が得られる.
右辺の16iを極形式で表すと
16(cos+i sin)
となるので,x4=16iの1つの解は
2(cos+i sin) この解を原点の周りにずつ回転すると他の3つの解が得られる. |

 |