|
■複素数平面
○ 複素数平面 x, yを実数として,複素数x+yiを座標平面上の点(x, y)で表したものを複素数平面という(複素平面,ガウス平面ともいう). 複素数平面は,右図1のように書く.(虚軸の目盛を1, 2, 3, ...で表すこともある.)
【例】 右図において
(1) 点Aは,虚数2+3iを表している. (2) 点Bは,虚数−2+iを表している. (3) 点Cは,実数4を表している. 一般に,実軸(横の軸,xy平面のx軸)上の点はx+0iすなわちxという実数を表す.原点よりも右側は正の数,左側は負の数になる.
(4) 点Dは,純虚数−3iを表している.一般に,虚軸(縦の軸,xy平面のy軸)上の点は0+yiすなわちyiという純虚数を表す.
(用語) 右図2に示すように,実数も虚数も複素数に含まれ,x+yi(x, yは実数)の形で表される最も広い範囲が複素数になる. 虚部yが0でないものを虚数といい,そのうちで特に実部xが0でかつ虚部yが0でないものを純虚数という. |
図1
  |



|
|
○ 共役複素数 複素数z=x+yi(ただし,x, yは実数)に対して,その虚部の符号だけ変えたものx−yiを,複素数zの共役複素数といい, で表す.
ある複素数zとその共役複素数とは,右図3のように実軸に関して線対称な位置にある.
【例】
(1) z=3+4iのとき=3−4i
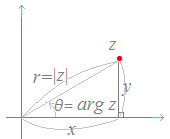
(2) =1−2i (3) =1+2i (4) ==1+2i ○ 絶対値 原点0から複素数z=x+yi(ただし,x, yは実数)までの距離を複素数zの絶対値といい,|z|で表す. |z|=≧0が成り立つ. ○ 偏角 複素数平面上の点Pが複素数zを表すとき,複素数OPが実軸の正の向きとなす角θを複素数zの偏角といい,arg zで表す. ○ 複素数の極形式 右図4のように,複素数z=x+yiの絶対値をr,偏角をθとするとき z=r(cosθ+isinθ) と表すことができる.この形を極形式という.
極形式で,0≦θ<2πとすれば,偏角はただ1通りに定まる・・・ただし,原点だけは偏角を考えない.
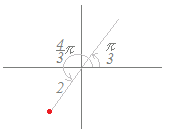
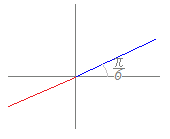
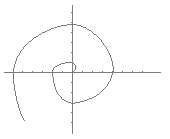
例えば,右図5の点は絶対値が2で偏角が として, 2(cos+isin) とするのが普通であるが,必要に応じてr≧0や0≦θ<2πという制限を緩めることがある. 【例】 右図6のような直線の方程式は θ= で表すことができるが,r≧0だけに制限すると青で示した半直線だけとなり,赤で示した部分を含めることができなくなる.このような場合にr<0となるときは,θで表される角から見て原点の反対側の点を表すとしておくと,この不自由を取り除くことができる. 【例】 右図7のような螺旋は r=θ で表すことができるが,その場合にθとしては2πよりも大きな値まで無限に考えることになる. |
図3
     |
| 問題2次の複素数を極形式で表してください.なお,r≧0,0≦θ<2πの範囲で定めてください. |
 右図のようにr==, θ=となるから
右図のようにr==, θ=となるから1+i=(cos+isin) |
 右図のようにr==2, θ=となるから
右図のようにr==2, θ=となるから1−i=2(cos+isin) なお,2(cos−isin) は値としては等しいが,極形式は必ずr(cosθ+isinθ)の形で書かなければならないので,不適当 |
|
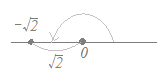 右図のようにr==2, θ=πとなるから
右図のようにr==2, θ=πとなるから−=(cosπ+isinπ) なお,(cosθ−isinθ) は値としては等しいが,極形式は必ずr(cosθ+isinθ)の形で書かなければならないので,不適当 |
|
 右図のようにr=3, θ=となるから
右図のようにr=3, θ=となるから3(cos+isin) なお,−3(cos+isin) は値としては正しいが,r≧0の形になっていないので不適当 |
|
|
問題3右の赤で示した複素数を極形式で表してください. なお,r≧0,0≦θ<2πの範囲で求めてください. 3(cos0+isin0) 3(cos0+isin0) 3(cos+isin ) 3(cos+isin ) 3(cos+isin ) 3(cos+isin ) 3(cos+isin ) 3(cos+isin ) 3(cosπ+isinπ ) 3(cosπ+isinπ ) 3(cos+isin ) 3(cos+isin ) 3(cos+isin ) 3(cos+isin ) 3(cos+isin ) 3(cos+isin ) |


|
|
|
|
|
問題4極形式で表された次の複素数を右の複素数平面上でポイントしてください.
(実部や虚部が整数にならないものは,目分量で測るものとし,そこそこ近ければ正解とします.) (※HELP1で文章が,HELP2で図が示されます) [第1問 / 全6問] 次の問題 HELP1 HELP2 |



|