内分点の内分点

【例１】
　右図３のように，複素数平面において，△ABCの頂点Aを表す複素数をz1，頂点Bを表す複素数をz2，頂点Cを表す複素数をz3とし，ABを2:3に内分する点をF，ACを3:4に内分する点をE，BEとCFの交点をPとする．
(1)Pを表す複素数をz1 , z2 , z3で表してください．
(2)BP:PE, CP:PFを求めてください．
(3)APの延長が線分BCと交わる点をDとするとき，CD:DB, AP:PDを求めてください．

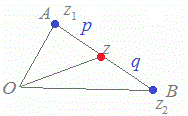
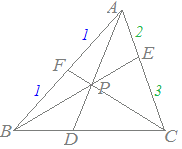
→ 携帯版は別頁 ■内分点の内分点【内分点の公式】　複素数平面において，２点A(z1 ), B(z2 )を結ぶ線分ABをp:qの比に内分する点を表す複素数は .qz1+pz2p+qnnnnnn （解説）　右図１のようになりますが，見かけの上で遠い方の比率を掛けたものが分子に来ます．【内分点の内分点】　複素数平面上に３点A(z1 ), B(z2 ), C(z3 )があるとき z=.pz1+qz2+rz3p+q+rnnnnnnnnn とすると， (1) ABをq:pに内分する点をFとするとき， zはCFを(q+p):rに内分する点になる． (2) BCをr:qに内分する点をDとするとき， zはADを(q+r):pに内分する点になる． (3) CAをr:pに内分する点をEとするとき， zはBEを(r+p):qに内分する点になる． (*) zはCF,AD, BEの交点を表す．（解説） (1) C:z3 , F:.qz1+pz2p+qnnnnnn だから z=.pz1+qz2+rz3p+q+rnnnnnnnnn=.(q+p).pz1+qz2q+pnnnnnn+rz3r+(q+p)nnnnnnnnnnnnnn のように変形すると，zはCFを(q+p):rに内分する点を表すことがわかります． (2) A:z1 , D:.qz2+rz3r+qnnnnnn だから z=.pz1+qz2+rz3p+q+rnnnnnnnnn=.pz1+(r+q).qz2+rz3r+qnnnnnn(r+q)+pnnnnnnnnnnnnnn のように変形すると，zはADを(r+q):pに内分する点を表すことがわかります．	図１図２ (3) B:z2 , E:.pz1+rz3r+pnnnnnn だから z=.pz1+qz2+rz3p+q+rnnnnnnnnn=.qz2+(r+p).pz1+rz3r+pnnnnnn(r+p)+qnnnnnnnnnnnnnn のように変形すると，zはBEを(r+p):qに内分する点を表すことがわかります． (*) 　(1)(2)(3)の結果から，zは３直線CF,AD, BEのいずれの上にもあるから，CF,AD, BEの交点を表す．
【例１】　右図３のように，複素数平面において，△ABCの頂点Aを表す複素数をz1，頂点Bを表す複素数をz2，頂点Cを表す複素数をz3とし，ABを2:3に内分する点をF，ACを3:4に内分する点をE，BEとCFの交点をPとする． (1)Pを表す複素数をz1 , z2 , z3で表してください． (2)BP:PE, CP:PFを求めてください． (3)APの延長が線分BCと交わる点をDとするとき，CD:DB, AP:PDを求めてください．（解答） (1)右図４のように，FからBEに平行な線を引き，ACと交わる点をGとすると AG:GE=2:3=8:12 AE:EC=4:5=20:25だから AG:GE:EC=8:12:25 したがって FP:PC=12:25 PはF(.3z1+2z25nnnnnn) , C(z3)を12:25に内分する点だから .25.3z1+2z25nnnnnn+12z337nnnnnnnnnnnnnn=.15z1+10z2+12z337nnnnnnnnnnnnn…（答） (2)(1)よりCP:PF=25:12…（答）また .15z1+10z2+12z337nnnnnnnnnnnnn=.27.15z1+12z327nnnnnnnn+10z237nnnnnnnnnnnnnn =.27.5z1+4z39nnnnnn+10z237nnnnnnnnnnnnnn と変形すると， PはE(.5z1+4z39nnnnnn) , B(z2)を10:27に内分する点であることがわかる． BP:PE=27:10…（答）	図３図４ (3) .15z1+10z2+12z337nnnnnnnnnnnnn=.15z1+22.10z2+12z322nnnnnnnn37nnnnnnnnnnnnnn =.15z1+22.5z2+6z311nnnnnn37nnnnnnnnnnnnnn と変形すると， PはA(z1) , D(.5z2+6z39nnnnnn)を22:15に内分する点であることがわかる． CD:DB=5:6…（答） AP:PD=22:15…（答）
【問題１】　右図５のように，複素数平面において，△ABCの頂点Aを表す複素数をz1，頂点Bを表す複素数をz2，頂点Cを表す複素数をz3とし，ABの中点をF，ACを2:3に内分する点をE，BEとCFの交点をPとする．（以下，正しいものを選んでください．） (1)Pを表す複素数をz1 , z2 , z3で表してください．解説 .z1+2z2+3z36nnnnnnnnn .3z1+z2+2z36nnnnnnnnn .3z1+3z2+2z38nnnnnnnnnn .2z1+3z2+3z38nnnnnnnnnn (2)BP:PE, CP:PFを求めてください．解説 BP:PE=3:2 BP:PE=4:3 BP:PE=5:3 BP:PE=5:4 解説 CP:PF=2:1 CP:PF=3:1 CP:PF=3:2 CP:PF=4:3 (3)APの延長が線分BCと交わる点をDとするとき，CD:DB, AP:PDを求めてください．解説 CD:DB=2:1 CD:DB=3:1 CD:DB=3:2 CD:DB=4:3 解説 AP:PD=1:1 AP:PD=3:2 AP:PD=4:3 AP:PD=5:3	図５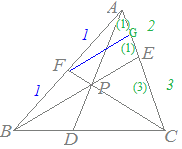右図のように，FからBEに平行な直線を引き，ACと交わる点をGとすると， AG:GE=1:1, GE:EC=1:3 となるから FP:PC=1:3 したがって .3.z1+z22nnnn+z34nnnnnnnn=.3z1+3z2+2z38nnnnnnnnnn .3z1+3z2+2z38nnnnnnnnnn=.3z2+5.3z1+2z35nnnnnn8nnnnnnnnnnn と変形できるから，PはB(z2 )とE(.3z1+2z35nnnnnn)とを5:3に内分します． (1)の結果から，CP:PF=3:1です． .3z1+3z2+2z38nnnnnnnnnn=.3z1+5.3z2+2z35nnnnnn8nnnnnnnnnnn と変形できるから，DはB(z2 )とC(z3 )とを2:3に内分します．（CD:DB=3:2） .3z1+3z2+2z38nnnnnnnnnn=.3z1+5.3z2+2z35nnnnnn8nnnnnnnnnnn から，PはA(z1 )とD(.3z2+2z35nnnnnn)とを5:3に内分します．
【問題２】　右図６のように，複素数平面において，△ABCの頂点Aを表す複素数をz1，頂点Bを表す複素数をz2，頂点Cを表す複素数をz3とし，ABを1:3に内分する点をF，ACを2:1に内分する点をE，BEとCFの交点をPとする．（以下，正しいものを選んでください．） (1)Pを表す複素数をz1 , z2 , z3で表してください．解説 .z1+3z2+6z310nnnnnnnnn .z1+6z2+3z310nnnnnnnnn .3z1+z2+6z310nnnnnnnnnn .3z1+6z2+z310nnnnnnnnnn (2)BP:PE, CP:PFを求めてください．解説 BP:PE=6:1 BP:PE=7:1 BP:PE=8:1 BP:PE=9:1 解説 CP:PF=2:3 CP:PF=2:5 CP:PF=3:4 CP:PF=4:5 (3)APの延長が線分BCと交わる点をDとするとき，CD:DB, AP:PDを求めてください．解説 CD:DB=1:6 CD:DB=1:7 CD:DB=1:8 CD:DB=1:9 解説 AP:PD=5:2 AP:PD=7:3 AP:PD=8:3 AP:PD=9:4	図６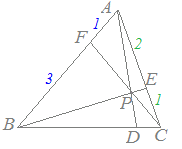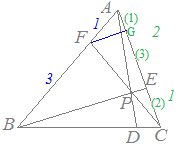右図のように，FからBEに平行な直線を引き，ACと交わる点をGとすると， AG:GE=1:3, AE:EC=2:1=4:2 だから GE:EC=3:2 FP:PC=3:2 したがって .2.3z1+z24nnnnn+3z35nnnnnnnnnn=.3z1+z2+6z310nnnnnnnnn .3z1+z2+6z310nnnnnnnnn=.z2+9.3z1+6z39nnnnnn10nnnnnnnnnnn と変形できるから，PはB(z2 )とE(.z1+2z33nnnnnn)とを9:1に内分します． (1)の結果から，CP:PF=2:3です． .3z1+z2+6z310nnnnnnnnnn=.3z1+7.1z2+6z37nnnnnn10nnnnnnnnnnn と変形できるから，DはB(z2 )とC(z3 )とを6:1に内分します．（CD:DB=1:6） .3z1+z2+6z310nnnnnnnnnn=.3z1+7.1z2+6z37nnnnnn10nnnnnnnnnnn から，PはA(z1 )とD(.1z2+6z37nnnnnn)とを7:3に内分します．