|
■軌跡の方程式2
【例1】
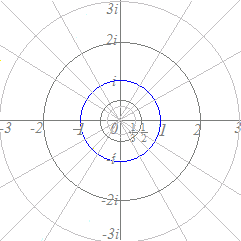
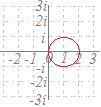
(解答)複素数z, wが|z|=1, w−2i=z+3を満たすとき,wが描く図形を調べてください. w−2i=z+3をzについて解くと z=w−3−2i ここで |z|=1だから |w−3−2i|=1 ゆえに,wは, 点3+2iを中心とする半径1の円を描く. |
○ ≪解き方≫
(1) zについての方程式
が与えられているとき(2) w=f(z)の形の関係式
(2)をz=g(w)の形の関係式に直して,(1)に代入するとwについての方程式が得られる.
 ○ 複素数の定数をαとするとき ○ 複素数の定数をαとするとき
|w−α|=r (r>0)
はαを中心とする半径rの円を表す.
 ○ 複素数の定数をαとするとき ○ 複素数の定数をαとするとき
w=z+α
の変換により,各々の点はαだけ平行移動した点に移される.
|
|
【例2】
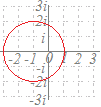
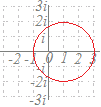
複素数z, wが|z−1|=1, w=2izを満たすとき,wが描く図形を調べてください. 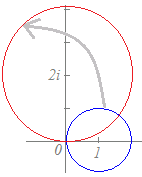 (解答) (解答)w=2izをzについて解くと z= ここで |z−1|=1に代入すると |−1|=1 |w−2i|=|2i|=2 ゆえに,wは, 点2iを中心とする半径2の円を描く. |
○ 2つの複素数をz1 , z2とするとき
(解説)
|z1z2|=|z1||z2|
が成り立つ.すなわち,積の絶対値は絶対値の積に等しい.
各々を極形式で表したとき z1=r1(cosθ1+i sinθ1) z2=r2(cosθ2+i sinθ2) になるとすれば z1z2=r1r2{cos(θ1+θ2)+i sin(θ1+θ2)} となるから,積z1z2の絶対値は,r1r2すなわち絶対値の積になる.(積z1z2の偏角は,偏角θ1 , θ2の和になる.)
⇒ 積z1z2は,複素数平面上で点z1を原点の周りにθ2だけ回転して,r2だけ拡大(縮小)した点になる.
左の【例2】では,2i=2(cos+i sin)だから,w=2izとなる点wはzを原点の周りにだけ回転して2倍した点になる.
一般に,複素数αの極形式がα=r(cosθ+i sinθ)となるとき,w=αzとなる変換によって,各々の点zは原点の周りに角θだけ回転してr倍した点に移される.
|
|
【例3】
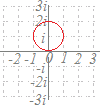
複素数zが|2z−1|=1 (z≠0)で表される円周上を動くとき,w=が描く図形を調べてください. 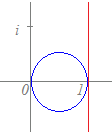 (解答) (解答)|2z−1|=1すなわち|z−|= は,点を中心とする半径の円を表す. このとき z=だから |−1|=1 |2−w|=|w| |w−2|=|w| ゆえに,wは, 原点と点2を結ぶ線分の垂直二等分線となる. すなわち直線x=1となる. |
○ 一般にw=となる変換は「反転」と呼ばれ,
|w|=だから,大きさは逆数になる.
したがって,原点を中心とする半径1の円(単位円)の中と外が逆になる.
w=だから,偏角は正負が逆になる.
したがって,上下が逆になる.
|
|
【例4】
(解説)複素数zが|z|=1 (z≠1)で表される円周上を動くとき, w= が描く図形を調べてください. zについて解くと wz−w=z+1 wz−z=w+1 (w−1)z=w+1 z= |z|=1の条件をwの式に直すと ||=1 |w+1|=|w−1| したがって, 1, −1を結ぶ線分の垂直二等分線 すなわち,y軸 |
(参考)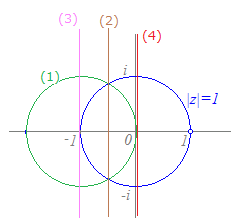
(1) z−1 :左に1平行移動
※ 一般に,複素数a, b, c, dを用いて
w=
で表される変換は,「平行移動」「回転・拡大」「反転」を組み合わせたものとなる.
(2) :反転 (3) :2倍に拡大 (4) +1 :右に1平行移動 |
|
問題各々正しいものを選んでください.
z=w+2+i
|z|=|w+2+i|=1 により,点−2−iを中心とする半径1の円になります.
z=
|z|=||=1 |w|=|1+i|= により,原点を中心とする半径の円になります.
z=
|z|=||=1 |w−1+i|=|i|=1 により,点1−iを中心とする半径1の円になります. 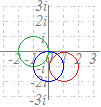 (別解) (別解)
1) 左へ1平行移動:z−1
により,右図のようになります.
2) 90°回転:i(z−1) 3) 右へ1平行移動:i(z−1)+1 |
wz−w=2i
z= |z|=||=1 |w+2i|=|w| により,原点0と点−2iを結ぶ線分の垂直二等分線 すなわち,直線y=−1になります. 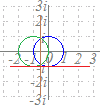 (別解) (別解)
1) 左へ1平行移動:z−1
2) 反転: 3) 90°回転して2倍に拡大: により,右図のようになります.
zについて解くと
wz−2w=3z
|z|=1だから
wz−3z=2w (w−3)z=2w z=
|z|=||=1
により,原点0と点3からの距離の比が1:2となるアポロニウスの円になる.|2w|=|w−3| 2|w|=|w−3| すなわち,原点0と点3を1:2に内分する点1と1:2に外分する点−3を直径の両端とする円になります. すなわち,−1を中心とする半径2の円になります.
zについて解くと
wz−w=−z+i
|z|=1だから
wz+z=w+i (w+1)z=w+i z=
|z|=||=1
により,点−iと点−1を結ぶ線分の垂直二等分線になる.|w+i|=|w+1| すなわち,直線y=xになります. |


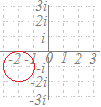
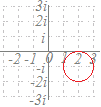
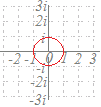
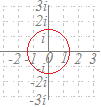
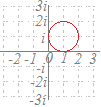

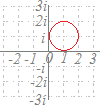
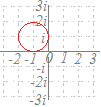
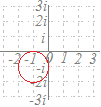
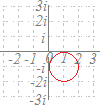
 で示した各点
で示した各点