|
○この頁では,それぞれの問題の結果を暗記することはお勧めしない.
【要点】○いろいろな問題を処理する中で「考え方や変形の仕方を身に付ける」ことが目標です.
2つの複素数の商(割り算)を極形式で書くと
A(α)からB(β)へ移るときの「辺の長さの比」と「回転角」が分かる.
【例題1.1】
3点O, A(α), B(β)を頂点とする△OABについて が成り立つとき△OABはどのような形の三角形か述べよ. 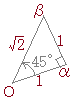 (解答)
(解答)A(α)を原点の周りに左回りに45°だけ回転して,さらに したがって,∠OABが直角となる直角二等辺三角形
この問題に答えるためには,辺の比が1:
このことに気づかない場合は, などと,AB間の距離も求める必要があります.
≪参考≫
そもそも,複素数で書かれた1つの等式は,実数で書かれた2つの等式と同値になります. ○1 実部,虚部で書けば
a+bi=c+di ←→
b=d ○2 極形式で書けば r1(cosα+isinα)=r2(cosβ+isinβ) (r1, r2>0, 0≦α, β<2π) ↓↑ α=β 直角二等辺三角形となるための条件は,実数(大きさ)を用いて |α|2+|β|2=|β−α|2…(*2) のように連立方程式で書いてもよいはずです.(問題の形によってはこの形の方が使いやすい場合もある)  (*1)(*2)と(2)とは次のようにつながる.
(*1)(*2)と(2)とは次のようにつながる.(*1)を(*2)に代入すると 2|α|2=|β−α|2 (*1)(*2)←→(*1)(*3)であるが,(*1)(*3)は これは,上記(i)で述べた を2つに分けて述べていることになる.
※以下の問題では,画面上で答えやすいように選択問題にしていますが,計算用紙を使ってよく考えてから正しい選択肢をクリックしてください.
なお,試験問題では単に「二等辺三角形」と答えるだけでは不十分で「AB=BCの二等辺三角形」などと答えなければなりませんが,選択肢は省略形になっています.詳しくは解説に書いたように答えるのが普通です. |
【問題1】
3点O, A(α), B(β)を頂点とする△OABについて
が成り立つとき△OABはどのような形の三角形か述べよ. と変形すると, 「  この問題に答えるためには,辺の比が1:2で,その間の角度が60°のときは,
この問題に答えるためには,辺の比が1:2で,その間の角度が60°のときは,「1: このことに気づかない場合は, などと,AB間の距離も求める必要があります.
(2)
3点O, A(α), B(β)を頂点とする△OABについて が成り立つとき△OABはどのような形の三角形か述べよ. と変形すると, 正三角形…(答) 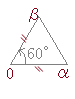 この問題に答えるためには,辺の比が1:1で,その間の角度が60°のときは,正三角形になるという中学校数学の基本が前もって分かっていなければなりません.
この問題に答えるためには,辺の比が1:1で,その間の角度が60°のときは,正三角形になるという中学校数学の基本が前もって分かっていなければなりません.このことに気づかない場合は, などと,AB間の距離も求める必要があります.
≪参考≫
そもそも,複素数で書かれた1つの等式は,実数で書かれた2つの等式と同値になります. 正三角形となるための条件は,実数(大きさ)を用いて |α|=|β−α|…(*2) のように連立方程式で書いてもよいはずです.(問題の形によってはこの形の方が使いやすい場合もある) (*1)の両辺を|α|で割ると (*2)の両辺を|α|で割ると 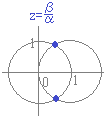 (*1)(*2)←→(*3)(*4)であるが,(*3)(*4)は
(*1)(*2)←→(*3)(*4)であるが,(*3)(*4)はしたがって,(*1)(*2)の2つに分けて述べている事柄は の1つで述べられる事柄と同じになる.(いずれも三角形ができるためには,α,β≠0が前提となっている) |
 (解答)
(解答)
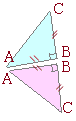
 2つの辺のなす角を考えるとき,(ベクトルの用語でいえば)始点をそろえた方が図形をイメージしやすくなります.
2つの辺のなす角を考えるとき,(ベクトルの用語でいえば)始点をそろえた方が図形をイメージしやすくなります. 2つの辺のなす角を考えるとき,(ベクトルの用語でいえば)始点をそろえた方が図形をイメージしやすくなります.
2つの辺のなす角を考えるとき,(ベクトルの用語でいえば)始点をそろえた方が図形をイメージしやすくなります.


 この問題は,この頁でここまで扱ってきた問題と少し違う点があることに注意.すなわち,ここまでの問題は「三角形の形が決まる」(大きさまでは決まらない)のに対して,この問題は三角形の形が完全には決まらない(不定の要素があります).
この問題は,この頁でここまで扱ってきた問題と少し違う点があることに注意.すなわち,ここまでの問題は「三角形の形が決まる」(大きさまでは決まらない)のに対して,この問題は三角形の形が完全には決まらない(不定の要素があります). 右図のように
右図のように 右図のように
右図のように