≪目が覚める1題≫
4つの複素数 z1, z2, z3, z4は互いに異なり,その絶対値はすべて 1であるとする.
(1) 略
(2) z1+z2+z3=0が成り立つとき, z1, z2, z3を頂点とする複素数平面上の三角形は正三角形であることを示せ.
(3) z1+z2+z3+z4=0が成り立つとき, z1, z2, z3, z4を頂点とする複素数平面上の四角形は長方形であることを示せ.
(お茶の水女子大2016年度)
式の変形:計算力で解決できる問題も多いが,図形の問題は図形によって解決する方が見通しが立てやすい.
ベクトルの問題はベクトルで,複素数の問題は複素数で,図形の問題は図形の知識で解く方が見通しを立てやすい!!
ベクトルで考えて,複素数 z1, z2, z3をベクトル  \( \displaystyle \vec{z_1},\hspace{5px}\vec{z_2},\hspace{5px}\vec{z_3} \) \( \displaystyle \vec{z_1},\hspace{5px}\vec{z_2},\hspace{5px}\vec{z_3} \)に対応させると
 \( \displaystyle \vec{z_1}+\vec{z_2}+\vec{z_3}=\vec{0} \) \( \displaystyle \vec{z_1}+\vec{z_2}+\vec{z_3}=\vec{0} \)
ならば, 各ベクトルのなす角が120°になることを示せばよい.
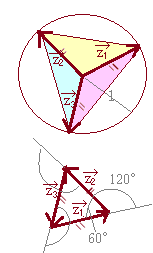
仮定により,  \( \displaystyle \vec{z_1} \) \( \displaystyle \vec{z_1} \)の終点に  \( \displaystyle \vec{z_2} \) \( \displaystyle \vec{z_2} \)の始点を,  \( \displaystyle \vec{z_2} \) \( \displaystyle \vec{z_2} \)の終点に  \( \displaystyle \vec{z_3} \) \( \displaystyle \vec{z_3} \)の始点を継いで行くと  \( \displaystyle \vec{z_3} \) \( \displaystyle \vec{z_3} \)の終点が原点に戻る.また,  \( \displaystyle \vec{z_1},\hspace{5px}\vec{z_2},\hspace{5px}\vec{z_3} \) \( \displaystyle \vec{z_1},\hspace{5px}\vec{z_2},\hspace{5px}\vec{z_3} \)の大きさ(長さ)はすべて1だから,右の下の図のように「3辺の長さが等しい」正三角形ができる.
正三角形の内角は60°だから,その外角は120°になり,ベクトル  \( \displaystyle \vec{z_1},\hspace{5px}\vec{z_2} \) \( \displaystyle \vec{z_1},\hspace{5px}\vec{z_2} \)のなす角は120°になる.同様にして,他の2組のベクトルのなす角も120°になる.
右の上の図において,黄色,水色,桃色で示した三角形はすべて2辺の長さが1でその間の角が120°であるから合同.よって頂点 z1, z2, z3をつないでできる三角形は正三角形になる.
ベクトルで考えて,複素数 z1, z2, z3, z4をベクトル  \( \displaystyle \vec{z_1},\hspace{5px}\vec{z_2},\hspace{5px}\vec{z_3},\hspace{5px}\vec{z_4} \) \( \displaystyle \vec{z_1},\hspace{5px}\vec{z_2},\hspace{5px}\vec{z_3},\hspace{5px}\vec{z_4} \)に対応させると
 \( \displaystyle \vec{z_1}+\vec{z_2}+\vec{z_3}+\vec{z_4}=\vec{0} \) \( \displaystyle \vec{z_1}+\vec{z_2}+\vec{z_3}+\vec{z_4}=\vec{0} \)
ならば, 四角形の内角がすべて90°になることを示せばよい.
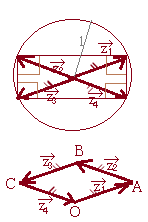
 \( \displaystyle \vec{z_1},\hspace{5px}\vec{z_2},\hspace{5px}\vec{z_3},\hspace{5px}\vec{z_4} \) \( \displaystyle \vec{z_1},\hspace{5px}\vec{z_2},\hspace{5px}\vec{z_3},\hspace{5px}\vec{z_4} \)の大きさはすべて1だから,右の下の図において四角形ABCDは ひし形になる.
頂点 z1, z2, z3, z4の並び方は指定されていないが,例えば右の下の図のように, z1, z2, z3, z4の順に左回りに並んでいる場合,
 \( \displaystyle \vec{z_1}=-\vec{z_3},\hspace{5px}\vec{z_2}=-\vec{z_4} \) \( \displaystyle \vec{z_1}=-\vec{z_3},\hspace{5px}\vec{z_2}=-\vec{z_4} \)
になる.
半径1の円において,大きさが1の2つのベクトル  \( \displaystyle \vec{z_1},\hspace{5px}\vec{z_3} \) \( \displaystyle \vec{z_1},\hspace{5px}\vec{z_3} \)が逆向きに入っているのだから,  \( \displaystyle \vec{z_1},\hspace{5px}\vec{z_3} \) \( \displaystyle \vec{z_1},\hspace{5px}\vec{z_3} \)は,右の上の図のように 直径になる.
直径の上に立つ円周角は90°だから ∠z1z2z3=90°, ∠z1z4z3=90°となる.
同様にして, ∠z2z1z4=90°, ∠z2z3z4=90°も言えるから,4つの 内角がすべて90°となり,長方形であることが示される.
(頂点 z1, z2, z3, z4の並び方が他の順である場合も同様にして示される)
*** この話は一般化できるものかどうか興味を引く問題である.5つの場合,6つの場合を検討してみよう ***
(4) 互いに異なる5つの複素数が|z1|=|z2|=|z3|=|z4|=|z5|=1
z1+z2+z3+z4+z5=0
を満たすとき,この五角形は正五角形といえるか?
(5) 互いに異なる6つの複素数が|z1|=|z2|=|z3|=|z4|=|z5|=|z6|=1
z1+z2+z3+z4+z5+z6=0
を満たすとき,この六角形は正六角形といえるか?
(4) 参考答案を見る
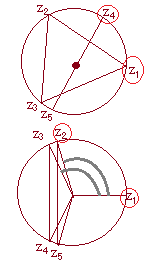
右図上のように z1, z2, z3が正三角形になるように並べておくと, z1+z2+z3=0になる.
これとは独立に z4, z5が直径になるように並べておくと, z4+z5=0になる.
そうすると,
(z1+z2+z3)+(z4+z5)=0
が成り立ち,正三角形と直径は独立に決められるから,五角形としては正五角形でも何でもないものになる.
また,右図下のように1つの頂点 z1=1を固定してから,  \( \displaystyle z_5=\bar{z_2},\hspace{5px}z_4=\bar{z_3} \) \( \displaystyle z_5=\bar{z_2},\hspace{5px}z_4=\bar{z_3} \)のように2組の共役複素数で4つの複素数 z2, z3, z4, z5を決めると,2つずつ共役だからこれらの和は実数になる.
次に, z2, z3の実部の和が  \( \displaystyle -\frac{1}{2} \) \( \displaystyle -\frac{1}{2} \)になるように決めると
例えば  \( \displaystyle z_2\!=\!-\!\frac{1}{12}\!+\! bi,\hspace{1px}z_5\!=\!-\!\frac{1}{12}-\!bi,\hspace{1px}z_3\!=\!-\!\frac{1}{6}\!+\! ci,\hspace{1px}z_4\!=\!-\!\frac{1}{6}\!-\!ci \) \( \displaystyle z_2\!=\!-\!\frac{1}{12}\!+\! bi,\hspace{1px}z_5\!=\!-\!\frac{1}{12}-\!bi,\hspace{1px}z_3\!=\!-\!\frac{1}{6}\!+\! ci,\hspace{1px}z_4\!=\!-\!\frac{1}{6}\!-\!ci \)
とおくと, z2+z3+z4+z5=−1になるから,
z1+(z2+z3+z4+z5)=0
となる.このように共役複素数の組を作って実部の和で調整するとできるから,正五角形とは関係ないものができる.
→右上に続く
|
(5) 参考答案を見る
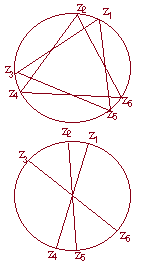
右図上のように z1, z3, z5が正三角形になるように並べておくと, z1+z3+z5=0になる.
これとは独立に z2, z4, z6が正三角形になるように並べておくと, z2+z4+z6=0になる.
そうすると,
(z1+z2+z3)+(z4+z5+z6)=0
が成り立ち,六角形としては正六角形でも何でもないものになる.
また,右図下のように互いに直径となる3組の複素数 z1, z4, z2, z5, z3, z6を作ると,それぞれ z1+z4=0, z2+z5=0, z3+z6=0となるから
(z1+z2)+(z3+z4)+(z5+z6)=0
を満たす.このとき六角形は正六角形でも何でもない.
(2)(3)(4)(5) そもそもの話
そもそも,複素数で書かれた1つの等式は,実数で書かれた2つの等式と同値になります.
○1 実部,虚部で書けば
a+bi=c+di ←→
 a=c a=c
b=d
○2 極形式で書けば
r1(cosα+isinα)=r2(cosβ+isinβ)
(r1, r2>0, 0≦α, β<2π)
↓↑
 r1=r2 r1=r2
α=β
○そこで(2)の問題のように z1, z2, z3で表される三角形の頂点を決めるには,
&chco=882200) \( \displaystyle z_1=r_1(\cos\theta_1+ i\sin\theta_1) \) \( \displaystyle z_1=r_1(\cos\theta_1+ i\sin\theta_1) \)
&chco=882200) \( \displaystyle z_2=r_2(\cos\theta_2+ i\sin\theta_2) \) \( \displaystyle z_2=r_2(\cos\theta_2+ i\sin\theta_2) \)
&chco=882200) \( \displaystyle z_3=r_3(\cos\theta_3+ i\sin\theta_3) \) \( \displaystyle z_3=r_3(\cos\theta_3+ i\sin\theta_3) \)
の6つの自由度  \( \displaystyle r_1,r_2,r_3,\theta_1,\theta_2,\theta_3 \) \( \displaystyle r_1,r_2,r_3,\theta_1,\theta_2,\theta_3 \)がある.
ここに大きさが1という条件を付ければ,  \( \displaystyle r_1=r_2=r_3=1 \) \( \displaystyle r_1=r_2=r_3=1 \)となるから,残り3つの変数  \( \displaystyle \theta_1,\theta_2,\theta_3 \) \( \displaystyle \theta_1,\theta_2,\theta_3 \)が自由になっている.
ここに1つの等式 z1+z2+z3=0を指定すると,自由度が2つ減って,1つの変数だけが自由に決められることになる.自由に決められる1つの変数とは例えば  \( \displaystyle \theta_1 \) \( \displaystyle \theta_1 \)( z1の偏角)である.
このようにして, z1+z2+z3=0を指定すると,
z1の偏角だけは自由に決められるが,残りはすべて決まることになる.

○これに対して(3)の問題のように z1, z2, z3, z4で表される四角形の頂点を決めるには,
&chco=882200) \( \displaystyle z_1=r_1(\cos\theta_1+ i\sin\theta_1) \) \( \displaystyle z_1=r_1(\cos\theta_1+ i\sin\theta_1) \)
&chco=882200) \( \displaystyle z_2=r_2(\cos\theta_2+ i\sin\theta_2) \) \( \displaystyle z_2=r_2(\cos\theta_2+ i\sin\theta_2) \)
&chco=882200) \( \displaystyle z_3=r_3(\cos\theta_3+ i\sin\theta_3) \) \( \displaystyle z_3=r_3(\cos\theta_3+ i\sin\theta_3) \)
&chco=882200) \( \displaystyle z_4=r_4(\cos\theta_4+ i\sin\theta_4) \) \( \displaystyle z_4=r_4(\cos\theta_4+ i\sin\theta_4) \)
の8つの自由度  \( \displaystyle r_1,r_2,r_3,r_4\theta_1,\theta_2,\theta_3,\theta_4 \) \( \displaystyle r_1,r_2,r_3,r_4\theta_1,\theta_2,\theta_3,\theta_4 \)がある.
ここに大きさが1という条件を付ければ,  \( \displaystyle r_1=r_2=r_3=r_4=1 \) \( \displaystyle r_1=r_2=r_3=r_4=1 \)となるから,残り4つの変数  \( \displaystyle \theta_1,\theta_2,\theta_3,\theta_4 \) \( \displaystyle \theta_1,\theta_2,\theta_3,\theta_4 \)が自由になっている.
ここに1つの等式 z1+z2+z3+z4=0を指定すると,自由度が2つ減って,2つの変数が自由に決められることになる.自由に決められる2つの変数とは例えば  \( \displaystyle \theta_1,\theta_2 \) \( \displaystyle \theta_1,\theta_2 \)( z1, z2の偏角)である.
右図において z1, z2の偏角は自由に定めることができ,その分だけ形は定まらない.
○同様にして,5つの点から五角形を作る場合,自由度が10のところが,大きさがすべて1という条件が付いていると自由度が5だけ減少し,さらに1つの等式 z1+z2+z3+z4+z5=0が指定されていると自由度が2だけ減少するから,結局自由度は3になる.したがって,例えば  \( \displaystyle \theta_1,\theta_2,\theta_3 \) \( \displaystyle \theta_1,\theta_2,\theta_3 \)のように3つの偏角が自由に決められることになり,形は定まらない.(どの問題でも,1つの頂点 z1の位置は自由に定められるが,五角形のこの問題では,さらに2つの角度が自由になり,形が定まらないということです.)
|
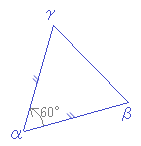
 点A(4z)を中心としてB(3z+2)を±60°回転するとC(z3)に重なればよい(右図青の線)
点A(4z)を中心としてB(3z+2)を±60°回転するとC(z3)に重なればよい(右図青の線)
 また,右図のように
また,右図のように ベクトルで考えて,複素数
ベクトルで考えて,複素数 ベクトルで考えて,複素数
ベクトルで考えて,複素数 右図上のように
右図上のように 右図上のように
右図上のように