|
【内分点の公式】
(解説)複素数平面において,2点A(z1 ), B(z2 )を結ぶ線分ABをp:qの比に内分する点を表す複素数は 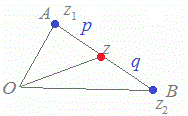
【内分点の内分点】
(解説)複素数平面上に3点A(z1 ), B(z2 ), C(z3 )があるとき z= とすると, (1)
ABをq:pに内分する点をFとするとき,
(2)
zはCFを(q+p):rに内分する点になる.
BCをr:qに内分する点をDとするとき,
(3)
zはADを(q+r):pに内分する点になる.
CAをr:pに内分する点をEとするとき,
(*)
zはBEを(r+p):qに内分する点になる.
zはCF,AD, BEの交点を表す.
 だから z== のように変形すると,zはCFを(q+p):rに内分する点を表すことがわかります. (2) A:z1 , D: だから z== のように変形すると,zはADを(r+q):pに内分する点を表すことがわかります. (3) B:z2 , E: だから z== のように変形すると,zはBEを(r+p):qに内分する点を表すことがわかります. (*) (1)(2)(3)の結果から,zは3直線CF,AD, BEのいずれの上にもあるから,CF,AD, BEの交点を表す. |


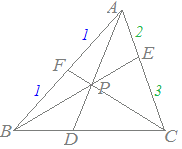
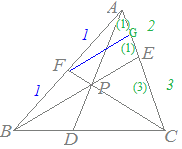 右図のように,
右図のように,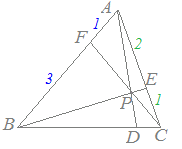
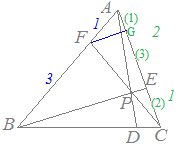 図のように,
図のように,