２直線の平行条件・垂直条件

← PC用は別頁

== ２直線の平行条件・垂直条件 ==

【２直線の平行条件】
　複素数平面上に４点A(z1 ), B(z2 ), C(z3 ), D(z4 ) があるとき，AB//CDとなるための条件は

z4−z3=k(z2−z1 )

となる実数kが存在すること．

k>0のときは同じ向きに平行

k<0のときは逆向きに平行

（解説）

--図１--

　図１において，ABを引き延ばして（または縮めて）CDを重なれば，AB//CDとなります．
　また，AB//CDならば，このような実数kが必ず定まります．

=（実数）と考えてもよい．

【３点が１直線上にあるための条件】
　複素数平面上に３点A(z1 ), B(z2 ), C(z3 )があるとき，これらの３点が１直線上にあるための条件は

z3−z1=k(z2−z1 )

となる実数kが存在すること．

0<k<1のときはA,C,Bの順に並ぶ

k>1のときはA,B,Cの順に並ぶ

k<0のときはC,A,Bの順に並ぶ

（解説）

--図２--

　図２の通り
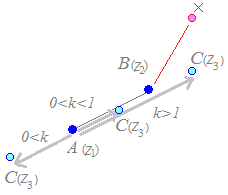　なお，赤で示したようにABを引き延ばして（または縮めて）ACに重ならなければ１直線上になく，１直線上になければABを引き延ばして（または縮めて）ACに重ならない．

=（実数）と考えてもよい．

【例１】
複素数平面上の４点A(−1+i), B(1+4i), C(3+3i), D(1+yi)について，AB//CDとなるように，実数yの値を定めてください．

（解答）
AB : 2+3i , CD : −2+(y−3)iだから
AB//CDとなるためには
2+3i=k{ −2+(y−3)i }
となることが条件となる．
2=−2k , 3=k(y−3)
より
y=0 (k=−1)…（答）

【例２】
複素数平面上の３点A(1+3i), B(i), C(x−i)が１直線上にあるように，実数xの値を定めてください．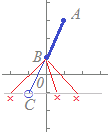

（解答）
AB : −1−2i , AC : (x−1)−4iだから
(x−1)−4i=k(−1−2i)
となることが条件となる．
x−1=−k , −4=−2k
より
x=−1 (k=2)…（答）

【２直線の垂直条件】
　複素数平面上に４点A(z1 ), B(z2 ), C(z3 ), D(z4 ) があるとき，AB⊥CDとなるための条件は

z4−z3=ki(z2−z1 )

となる実数kが存在すること．

（解説）

--図３--

AB : z2−z1 , CD : z4−z3だから
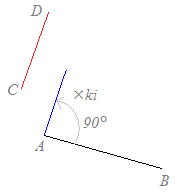i(z2−z1 )
はABを反時計回りに回転したものになる．
したがって，
ア）　k>0のときは，反時計回りに回転して拡大縮小したものがCDと一致する．
イ）　k<0のときは，時計回りに回転して拡大縮小したものがCDと一致する．
　いずれの場合も，
z4−z3=ki(z2−z1 )　（kは実数）
となれば，AB⊥CDとなる．

=（純虚数）と考えてもよい．

【例３】
複素数平面上の３点A(i), B(3+2i), C(x)について，AC⊥BCとなるように，実数xの値を定めてください．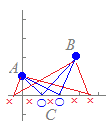

（解答）
AC : x−i , BC : (x−3)−2iだから
(x−3)−2i=ki(x−i)　（kは実数）
となることが条件となる．
x−3=k , −2=kx
−2=(x−3)x
x2−3x+2=0
(x−1)(x−2)=0
x=1, 2
より
x=1, 2 (k=−2, −1)…（答）

【例４】
複素数平面上の３点A(z1 ), B(z2 ), C(z3 )について，
z3−z1=(1+i)(z2−z1)
が成り立つとき，AB⊥BCとなることを示してください．

（解答）
BC : z3−z2
に，z3=(1+i)(z2−z1 )+z1=(1+i)z2−iz1
を代入すると
z3−z2=(1+i)z2−iz1−z2
=iz2−iz1=i(z2−z1 )
となるから
AB : z2−z1 を90°回転したものがBC : z3−z2になる．

【問題】

(1)複素数平面上の４点A(−1+2i) , B(1+3i) , C(1+2i) , D(2)について，次のうちで正しいものを選んでください．
解説

AB//CD AB⊥CD AC//BD AC⊥BD

AB : 2+i , CD : 1−2i

==i　（＝純虚数）

だから
AB//CDは不成立
AB⊥CDは成立
AC : 2 , BD : 1−3i

==　（≠実数，≠純虚数）

だから
AC//BDは不成立
AC⊥BDは不成立

(2)複素数平面上の４点A(1+i) , B(−1+4i) , C(−2+3i) , D(2+yi)について，AB//CDとなるように実数yの値を定めてください．
解説

y=−3 y=−2 y=2 y=3

AB : −2+3i , CD : 4+(y−3)i
だから
4+(y−3)i=k(−2+3i)
より
4=−2k , y−3=3k
y=−3 (k=−2)…（答）

(3)複素数平面上の４点A(1+i) , B(−1+4i) , C(−2+3i) , D(x+5i)について，AB⊥CDとなるように実数xの値を定めてください．
解説

x=−2 x=−1 x=1 x=2

AB : −2+3i , CD : (x+2)+2i
だから
(x+2)+2i=ki(−2+3i)=−3k−2ki
より
x+2=−3k , 2=−2k
x=1 (k=−1)…（答）

(4)３点A(−1+3i) , B(4−2i) , C(x+2i)が１直線上にあるように実数xの値を定めてください．
解説

x=0 x=1 x=2 x=3

AB : 5−5i , AC : (x+1)−i
だから
(x+1)−i=k(5−5i)=5k−5ki
となるには
x+1=5k , −1=−5k

x=0 (k=)…（答）

(5)複素数平面上の３点A(z1 ), B(z2 ), C(z3 )について，
z3−z1=(1+i)(z2−z1)
が成り立つとき，次のうち正しいものを選んでください．
解説

３点A,B,Cは１直線上にある

AB⊥BC AC⊥CB BA⊥AC

z3=(1+i)(z2−z1)+z1=(1+i)z2−iz1
を代入すると
z3−z2=i(z2−z1)
となるから
AB⊥BC…（答）

(6)複素数平面上の３点A(−2+2i), B(4+4i), C(x)について，ABを直径の両端とする円周上に点Cがくるように実数xの値を定めてください．
解説

x=0, 1 x=0, 2 x=1, 2 x=1, 3

AC⊥BCとなればよい．
AC : (x+2)−2i
BC : (x−4)−4i
だから
(x−4)−4i=ki{ (x+2)−2i }=2k+(x+2)ki
より
x−4=2k , −4=(x+2)k
x=2k+4を代入してkの２次方程式を解くと
−4=(2k+4+2)k
k2+3k+2=0
(k+1)(k+2)=0
k=−1, −2
このとき
x=2 , 0

［注］直前にPC版から入られた場合は，自動転送でスマホ版に来ていますので，ブラウザの［戻るキー］では戻れません（堂々巡りになる）．下記のリンクを使ってメニューに戻ってください．

...（携帯版）メニューに戻る

...（PC版）メニューに戻る