 【要点】
【要点】
△ ABCの面積は
 \( \displaystyle S=\frac{1}{2}AB\cdot AC\sin \theta \) \( \displaystyle S=\frac{1}{2}AB\cdot AC\sin \theta \)
で求められる.
 \( \displaystyle S=\frac{1}{2}BC\cdot BA\sin \phi \) \( \displaystyle S=\frac{1}{2}BC\cdot BA\sin \phi \)
でもよい
そこで,複素数平面上で A(z1), B(z2), C(z3)であるとき,△ ABCの面積を求めるには
 \( \displaystyle AB=|z_2-z_1| \) \( \displaystyle AB=|z_2-z_1| \)
 \( \displaystyle AC=|z_3-z_1| \) \( \displaystyle AC=|z_3-z_1| \)
) \( \displaystyle \theta=arg(\frac{z_3-z_1}{z_2-z_1}) \) \( \displaystyle \theta=arg(\frac{z_3-z_1}{z_2-z_1}) \)
を使って計算すればよい.
【例題2.1】
複素数 zを z=1+2iとする.複素数平面上で, 1, z, z2を表す点をそれぞれ, A, B, Cとするとき, ∠BACの大きさは オであり,三角形 ABCの面積は カである.
(広島工業大2005年)
 (解答)
(解答)
 \( \displaystyle \frac{z^2-1}{z-1}=z+ 1=2+2i \) \( \displaystyle \frac{z^2-1}{z-1}=z+ 1=2+2i \)
) \( \displaystyle =2\sqrt{2}(\cos\frac{\pi}{4}+ i\sin\frac{\pi}{4}) \) \( \displaystyle =2\sqrt{2}(\cos\frac{\pi}{4}+ i\sin\frac{\pi}{4}) \)
だから
∠BAC= \( \displaystyle \frac{\pi}{4} \) \( \displaystyle \frac{\pi}{4} \)
になる.
三角形の面積は
 \( \displaystyle S=\frac{1}{2}AB\cdot AC\sin\frac{\pi}{4} \) \( \displaystyle S=\frac{1}{2}AB\cdot AC\sin\frac{\pi}{4} \)
ここでAB=|2i|=2, AC=2× \( \displaystyle 2\sqrt{2}=4\sqrt{2} \)だから \( \displaystyle 2\sqrt{2}=4\sqrt{2} \)だから
 \( \displaystyle S=\frac{1}{2}\times 2\times 4\sqrt{2}\times\frac{1}{\sqrt{2}}=4 \) \( \displaystyle S=\frac{1}{2}\times 2\times 4\sqrt{2}\times\frac{1}{\sqrt{2}}=4 \)
【問題2】
(1)
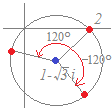
複素数 zが |z|=2を満たすとき,複素数平面上の4点 0, z, (1+i)z, 2izを頂点とする四角形の面積を求めよ.ただし, iは虚数単位とする.
(武蔵工業大2005年)

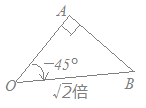
&chco=aa4422) \( \displaystyle 1+ i=\sqrt{2}(\cos \frac{\pi}{4}+ i\sin\frac{\pi}{4}) \) \( \displaystyle 1+ i=\sqrt{2}(\cos \frac{\pi}{4}+ i\sin\frac{\pi}{4}) \)だから, (1+i)zは zの大きさを  \( \displaystyle \sqrt{2} \) \( \displaystyle \sqrt{2} \)倍して  \( \displaystyle \frac{\pi}{4} \) \( \displaystyle \frac{\pi}{4} \)回転したものになる.
右図の △OABの面積は
 \( \displaystyle S_1=\frac{1}{2}\times OA\times OB\times \sin\frac{\pi}{4} \) \( \displaystyle S_1=\frac{1}{2}\times OA\times OB\times \sin\frac{\pi}{4} \)
 \( \displaystyle =\frac{1}{2}\times 2\times 2\sqrt{2}\times\frac{1}{\sqrt{2}}=2 \) \( \displaystyle =\frac{1}{2}\times 2\times 2\sqrt{2}\times\frac{1}{\sqrt{2}}=2 \)
&chco=aa4422) \( \displaystyle 2i=2(\cos \frac{\pi}{2}+ i\sin\frac{\pi}{2}) \) \( \displaystyle 2i=2(\cos \frac{\pi}{2}+ i\sin\frac{\pi}{2}) \)だから, 2izは zの大きさを  \( \displaystyle 2 \) \( \displaystyle 2 \)倍して  \( \displaystyle \frac{\pi}{2} \) \( \displaystyle \frac{\pi}{2} \)回転したものになる.
右図の △OBCの面積は
 \( \displaystyle S_2=\frac{1}{2}\times OB\times OC\times \sin\frac{\pi}{4} \) \( \displaystyle S_2=\frac{1}{2}\times OB\times OC\times \sin\frac{\pi}{4} \)
 \( \displaystyle =\frac{1}{2}\times 2\sqrt{2}\times 4\times\frac{1}{\sqrt{2}}=4 \) \( \displaystyle =\frac{1}{2}\times 2\sqrt{2}\times 4\times\frac{1}{\sqrt{2}}=4 \)
合計で 2+4=6
|
 (解答)
(解答)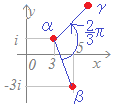 点
点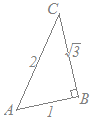
 点
点
 (解答)
(解答)