|
【要点1】
(解説)異なる2つの複素数z1 , z2が与えられていて,実数p, qが p+q=1, p≧0, q≧0 の条件を満たしながら変化するとき, z=pz1+qz2 で示される点は,2点z1 , z2を結ぶ線分になる. 
図1
図1のように,複素数z1に実数pを掛けたものpz1は,z1を同じ方向にp倍した点になります.
 p>0のときは同じ向きに,p<0のときは逆向きになります.また,p>1ならば拡大,0<p<1ならば縮小になります.
図2
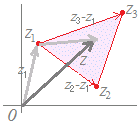
図2のように,2つの複素数z1 , z2の和z1+z2は,ベクトルの和と同様に図示することができます.すなわち,
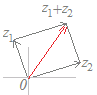 1) 平行四辺形の対角線で考える方法
原点とz1 , z2から.平行四辺形を作り,その対角線が和になる. 2) 三角形で考える方法
まず,原点からz1まで移動し,z2で表される分の移動を継ぎ足す.
図3
図3のように,2つの複素数z1 , z2の差z2−z1は,ベクトルの差と同様に図示することができます.すなわち,z1からz2に向かうものとなります.
 z2−z1によってできる複素数は,「(終点)−(始点)」の形になっています.向きを逆に覚えてしまう人が結構多いので,気をつけましょう.
複素数は,ベクトルで言えば「位置ベクトル」に対応しており,得られた複素数z2−z1を表す点は,図の赤丸のように原点からz2−z1だけ移動した点になります.
≪要点1の解説≫
図4
z=pz1+qz2(p+q=1, p≧0, q≧0)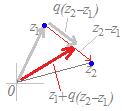 を書き換えると z=pz1+qz2(p=1−q, 0≦p≦1, 0≦q≦1) z=(1−q)z1+qz2(0≦q≦1) z=z1+q(z2−z1)(0≦q≦1) となるから,図4のように,まずz1まで進み,次にz2−z1を0≦q≦1倍だけ足したものになります.q=0のとき点z1を,q=1のとき点z2を表し,その間の値ではz1,z2の間の点を表します.
z=pz1+qz2(p+q=1, p≧0, q≧0)
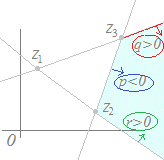
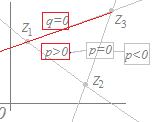
で表される複素数は,線分z1z2に埋め込まれたものを表しているのでなく,原点から線分z1,z2上の1点に向かっていることに注意 なお, z=pz1+qz2(p+q=1, p>0, q>0) となるときは,両端を含まない線分z1z2なります. z=pz1+qz2(p+q=1) だけの場合は,直線z1z2なります.(図5)
図5
(要点1の別の考え方)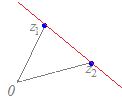 z=pz1+qz2(p+q=1, p>0, q>0) のとき,p+q=1だから, z= と書ける.これは,z1, z2をq:p=q:(1−q)に内分する点を表している.qが0<q<1の範囲で変化するとき,この値はz1z2間にある点を表す.q=0, 1のときは,元の式から線分の両端z1, z2になることがわかる. |
|
【例1】
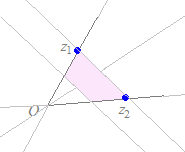
(解答)異なる2つの複素数z1 , z2が与えられていて,実数p, qが p+q=, p≧0, q≧0 の条件を満たしながら変化するとき, z=pz1+qz2 で示される点は,どのような図形を描くか? p+q= → p=−qを代入すると z=(−q)z1+qz2=z1+q(z2−z1) …(A) ただし, p=−q≧0, q≧0より0≦q≦ …(B) (A)(B)より,次の図の青で示した線分(両端を含む)  z=(p+q)=, p≧0, q≧0 と変形できるから,z1 , z2の内分点(上図の茶色の部分)の絶対値を半分にしたもの.青で示した線分(両端を含む) |
|
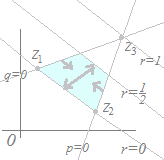
【例2】
(解答)異なる2つの複素数z1 , z2が与えられていて,実数p, qが p+q<1, p>0, q>0 の条件を満たしながら変化するとき, z=pz1+qz2 で示される点は,どのような図形を描くか? z=(p+q), p>0, q>0 と変形できるから,z1 , z2の内分点を縮小(p+q<1)したもの. すなわち,三角形O, z1 , z2の内部(周上は含まない) 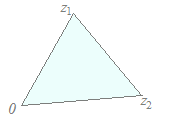 |





 ※
※ ※
※ ※
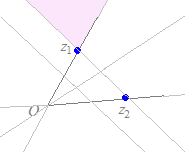
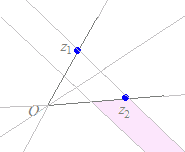
※ 上記の解説で,
上記の解説で,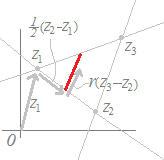






 図参照
図参照