|
���Z�`��w��b�̐��w�p��.����.��
|
�������䋉�� ��(�[�[�^)�� �_�����x�[���̔���@ �R�[�V�[�̔���@ ���[�x�̔���@ �������Ǝ������a |
|
[�d�v]
�@���������̒�`�̏��߂̕����u�O���珇�Ɂv�Əq�ׂ����Ƃɂ́C�Ӗ�������D���Ȃ킿�C�L������̘a�Ƃ͈قȂ�C���������́u�������̏���������ɕς�����v�u����Ɋ��ʂ�t���Ċ������Ɍv�Z������v����ƁC���ʂ��ς���Ă��܂��D• �L������̘a�Ƃ͈قȂ�C���������͂��̕��ѕ��ɏd�v�ȈӖ�������D • ���������̘a�����߂�Ƃ��C�������̏���������ɕς�����C����Ɋ��ʂ�t���Ċ������Ɍv�Z�����肵�Ă͂����Ȃ��D • �悎�����a�����߂Ă���C���̋Ɍ��ׂ�̂��|�C���g�D �@���̂��߁C���������̌v�Z������Ƃ��́C�����Ɂu�O���珇�Ɂv�����čs���Ȃ���Ȃ�Ȃ��D�����Ɛ��m�Ɍ����ƁC���������̌v�Z������ɂ́C�܂��u�悎�����a�v�����߂āC���̒l���ǂ̂悤�`�Ŗ����ɑ傫���Ȃ��Ă��C�u�悎�����a�v�����̒l�ɋߕt�����ǂ����ׂȂ���Ȃ�Ȃ��D �@���̂悤�ɁC ��1
�A) ���߂���Q���g�ݍ��킹�ď����� �C) ���߂�1�ȊO���Q���g�ݍ��킹�ď����� �A�j�C�j�̂ǂ��炪���������H���͗����Ƃ��Ԉ���Ă���D�A�j�C�j�Ƃ��u�O���珇�Ɂv�������ɁC�u�������̏���������ɕς��Ă���v�̂��ԈႢ�̌����ł��D �������́C���̂悤�Ɂu��n�����a�v���g���ċ��߂�D
��~�j�����ŌX�������ށ�
1) n����̂Ƃ��C��n�����a����1���܂ł̘a�F1 ��2���܂ł̘a�F1−1=0 ��3���܂ł̘a�F1−1+1=1 ��4���܂ł̘a�F1−1+1−1=0 →0��1�����ɏo�Ă��� 2) n�������̂Ƃ��C��n�����a�� n������Ȃ��傫���Ȃ�Ƃ��C�i����������ǂ��܂ł��o�ꂷ�邩��j��Ԗڂ܂ł̘a�Ƌ����Ԗڂ܂ł̘a����v���Ȃ�����C���������͎������Ȃ��D �@���̖��������̘a�͑��݂��Ȃ��D |
��2
��ʍ����A)�@�R�������Ă����� �C)�@���߂̂P�ȊO���R�������Ă����� �E�j ���߂̂Q�ȊO��3�������Ă����� �A�j�C�j�E�j�̂ǂ��炪���������H�������C�S���Ԉ���Ă���D�u�O���珇�Ɂv�������ɁC�u�������̏���������ɕς��Ă���v�̂��ԈႢ�̌����ł��D �������́C���̂悤�Ɂu��n�����a�v���g���ċ��߂�D 1) n=3k+1(k��0�ȏ�̐���)�̂Ƃ��C�m��L�̃C�j���n��n�����a�� 2) n=3k+2(k��0�ȏ�̐���)�̂Ƃ��C�m��L�̃E�j���n��n�����a�� 3) n=3k(k�͐��̐���)�̂Ƃ��C�m��L�̃A�j���n��n�����a�� n������Ȃ��傫���Ȃ�Ƃ��Cn��3�Ŋ������]��ɂ���ĈقȂ�l�ɂȂ邩��C���������͎������Ȃ��D |
|
�y��1.1�z
�i�j�@�������� |
�y��1.2�z
�i�j�@�������� ���������āC���̖��������͔��U���� �y��2.3�z�̂悤�ɃĊ��Ɣ�r���Ă��悢�D |
|
�y��2.1�z
�@��������
�������邱�Ƃ������ɂ́C|����|��1���������Ȗ������䋉���Ɣ�r�ł�����悢�D
�i�j���U���邱�Ƃ������ɂ́C|����|��1�����傫�Ȗ������䋉���Ɣ�r�ł�����悢�D �E�ӂ̑�1���͒萔�ŁC��2���͎������邩��C���ӂ��������� �y��4.2�z�̂悤�ɃR�[�V�[�̔���@��p���Ă������� |
�y��2.2�z
�@��������
�Ċ�(s=2)�Ɣ�r�ł����玦����
�i�j�E�ӂ̑�1���͒萔�ŁC��2���͎������邩��C���ӂ��������� |
|
�y��2.3�z
�@��������
�Ċ�(s=1)�Ɣ�r�ł����玦����
�i�j�E�ӂ͔��U���邩��C���ӂ����U���� �y��1.2�z�̂悤�Ɏ����Ă��悢�D
�y��2.4�z
�@�������� 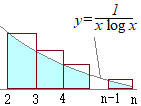 �E�}�Œ��F�̊K�i��}�`�̖ʐς͐��F�̖ʐς����傫������
�E�}�Œ��F�̊K�i��}�`�̖ʐς͐��F�̖ʐς����傫������������ �����疳�����������U���� |
�y��2.5�z
�@��������  �E�}�Ő��F�̖ʐς͔Z�����F�̊K�i��}�`�̖ʐςƔ������F�̊K�i��}�`�̊Ԃɂ��邩��
�E�}�Ő��F�̖ʐς͔Z�����F�̊K�i��}�`�̖ʐςƔ������F�̊K�i��}�`�̊Ԃɂ��邩�������� �ik=1�̂Ƃ��́y��2.4�z�̒ʂ�Dk��1�̂Ƃ��͈ȉ��̂悤�ɂȂ�j ���������� �A) 0<k<1�̂Ƃ��C �C) k>1�̂Ƃ��C �ȏ���܂Ƃ߂�ƁC�A)����сy��2.4�z����C0<k��1�̂Ƃ��C���U����D�C)����Ck>1�̂Ƃ���������D |
|
�y��3.1�z
�i�j�@�������� �_�����x�[���̔���@(2)�ɂ���������
�y��3.2�z
�i�j�@ �_�����x�[���̔���@(2)�ɂ��C
�y��3.3�z
�i�j�@�������� �_�����x�[���̔���@(2)�ɂ��C���̖��������͎�������D |
�y��3.4�z
�i�j�@�������� �_�����x�[���̔���@(2)�ɂ��C���̖��������͎�������D
�y��3.5�z
�i�j�@�������� �_�����x�[���̔���@(2)�ɂ��C���̖��������͎�������D
�y��3.6�z
�i�j�@�������� �_�����x�[���̔���@(2)�ɂ��C���̖��������͎�������D |
|
�y��4.1�z
�i�j�@�������� �R�[�V�[�̔���@(2)�ɂ���������D |
�y��4.2�z
�i�j�@�������� �R�[�V�[�̔���@(2)�ɂ���������D |
|
�y��5.3�z
�i�j�@�������� �_�����x�[���̔���@�ɂ�� ������
���̋����́C
��
�y��5.4�z
�i�j�@�������� �_�����x�[���̔���@�ɂ�� ������ |
�y��5.5�z
�i�j�@�������� �_�����x�[���̔���@�ɂ�� ������ |