|
���Z�`��w��b�̐��w�p��.����.��
=== ���̃y�[�W�̖ڎ� ===
��������(series)�������� �����������������邽�߂̕K�v���� ��r����@ ��r�ɂ悭�p�����鐳������ �������䋉�� ��(�[�[�^)�� �_�����x�[���̔���@ �R�[�V�[�̔���@ ���[�x�̔���@ �������Ǝ������a ��������
�@���������������Ƃ����D�������������L����p���� �Ƃ��������D �G�k
�@���Z�̐��w�̋��ȏ��ł́C��������̘a�̂��Ƃ��u���������v�Ƃ����D����ɑ��āC��w�̋��ȏ��ł́C���������̂��Ƃ�P�Ɂu�����v�Ƃ������Ƃ�����D�����ƌ����Ζ��������̏ȗ��Ȃ̂ŁC�w�L�������x�Ƃ������̂͂Ȃ��D����̑�n���܂ł̗L�����̘a�Ƃ������̂�\���ɂ́C���ɏq�ׂ�u��n�����a�v�Ƃ����p����g���D
��n�����a
�@�������������ƁC�����P�̐��� ��������D���̂Ƃ��C ���������̘a
�@��n�����a�̐����@��n�����a�̐��� �G�k
�@�u�����v�Ɓu�����̘a�v�̊W�́C�u����v�Ɓu����̘a�v�̊W�ƑS�R�Ⴄ���Ƃɒ��ӁI
�@���Ȃ킿�C����̘a�͊���̍��̘a |
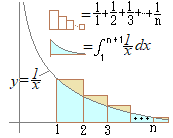 2)
2) s>0, ≠1�̑��̒l�̏ꍇ���C���l�ɂ��Ē�ϕ��Ƃ̔�r�ɂ���Ď�����D
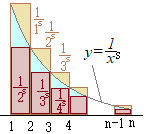
s>0, ≠1�̑��̒l�̏ꍇ���C���l�ɂ��Ē�ϕ��Ƃ̔�r�ɂ���Ď�����D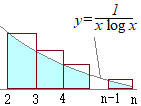 �E�}�Œ��F�̊K�i��}�`�̖ʐς͐��F�̖ʐς����傫������
�E�}�Œ��F�̊K�i��}�`�̖ʐς͐��F�̖ʐς����傫������ �E�}�Ő��F�̖ʐς͔Z�����F�̊K�i��}�`�̖ʐςƔ������F�̊K�i��}�`�̊Ԃɂ��邩��
�E�}�Ő��F�̖ʐς͔Z�����F�̊K�i��}�`�̖ʐςƔ������F�̊K�i��}�`�̊Ԃɂ��邩��