|
�����̘A����
�y�A���̒�`�z
�@ �P�ϐ�x�̊�y=f(x)���Cx=a�ɂ����ĘA���ł���Ƃ́C���̂R�̏�������������邱�Ƃ������܂�
(1)�@���lf(a)�����݂��邱��
(2)�@�Ɍ��lf(x)�����݂��邱�� (3)�@(1)(2)������������ 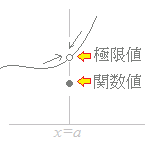 �E�}�́��Ŏ������Ɍ��l
�E�}�́��Ŏ������Ɍ��lf(x)�́C���m�ɂ�x�� a�łȂ��l���Ƃ�Ȃ���a�Ɍ���Ȃ��߂Â��Ƃ��̖ڕW�l��\���Ă���Ca�̎��ӂł̊��̃O���t�̗l�q�ɑΉ����Ă��܂��D���̋Ɍ��l�́C���lf(a)�Ƃ͖��W�ɒ�`�����Ƃ��낪�d�v�ł��D �E�}�́��Ŏ��������lf(a)�́Cx��a���������Ƃ��̒l�ł��D �����́C���Ɓ�����v����Ƃ��ɁCx=a�ɂ����ăO���t���u�Ȃ���v���ƂɂȂ�C�u�A���v�ł���Ƃ����܂��D
�y��z
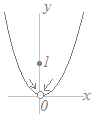 �ɂ���Ē�`������f(x)�ɂ��ẮC
�ɂ���Ē�`������f(x)�ɂ��ẮC
(1)�@���l��f(0)=1
(2)�@�Ɍ��l��f(x)=x2=0 �ł��邪�C(1)(2)���������Ȃ��̂�x=0�ɂ����ĕs�A���ł��D
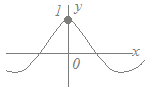 �ɂ���Ē�`������f(x)�ɂ��ẮC
�ɂ���Ē�`������f(x)�ɂ��ẮC
(1)�@���l��f(0)=1
(2)�@�Ɍ��l��f(x) ==1 �ƂȂ�C(1)(2)����v����̂�x=0�ɂ����ĘA���ł��D
����16�N�x�Z�p�m��ꎟ�������m���ʖ��n
�y���w�z�V-3
2a=1�̂Ƃ��Cf(x)�͘A���ƂȂ�D 3a�̒l�ɂ�����炸�Cf(x)�͘A���ƂȂ�D 4a�̒l�ɂ�����炸�Cf(x)�͘A���łȂ��D 5a�̒l�ɂ�����炸�Cf(x)�̘A�����̔���͂ł��Ȃ��D HELP
x��0�̂Ƃ��C����C���q�Ƃ��A�����ŕ����0�ɂȂ�Ȃ�����C�A���������ɂȂ�̂�x=0�ɂ��Ă���
=1������ a=1�̂Ƃ��C�����̏ꍇ�����A���ƂȂ� → 2 |
�����̕łɓo�ꂷ��y���z�́C���v�Вc�@�l���{�Z�p�m��̃z�[���y�[�W�Ɍf�ڂ���Ă���u�Z�p�m��ꎟ�����ߋ���� ���ʉȖ�A ���w�v�̈��p�ł��D�i=���\���ꂽ���앨�̈��p�j
���y����z�͌l�̎��Ăł����C�v�������މ��ɂ������āu���̓]�L�~�X�v�u�l�����̊ԈႢ�v�u�v���O�����̍쓮�~�X�v�Ȃǂ��܂܂��ꍇ�����蓾�܂��D �@�������ɂ��Ă̎��ⓙ�́C������҂�ς킹�邱�ƂȂ��C���v�������ނ̍쐬�ҁi<���>�j�ɑ��čs���Ă��������D
�y�Q�ϐ����ɂ�����A���̒�`�z
�@ �Q�ϐ�x, y�̊�z=f(x, y)���C(x,y)=(a,b)�ɂ����ĘA���ł���Ƃ́C���̂R�̏�������������邱�Ƃ������܂�
(1)�@���lf(a,b)�����݂��邱��
�������C(2)�ɂ�����f(x,y)��(x,y)��(a,b)�Ԃ̋�����0(2)�@�Ɍ��lf(x,y)�����݂��邱�� (3)�@(1)(2)������������ �ɋ߂Â��Ƃ��̋Ɍ���\�����̂Ƃ��܂��D
�߂Â����ɂ���ẮC�Ɍ����K��������v���Ȃ��̂ŁC�ǂ�ȋ߂Â��������Ă���̒l�ɋ߂Â��Ƃ��ɋɌ��l������Ƃ����D���̔��f�͂Q�_�Ԃ̋�����0�ɋ߂Â��ꍇ�ɂǂ��Ȃ邩�ōs���悢�D
�y��z
f(x,y)=�ɂ���Ē�`������f(x,y)�ɂ��� (x,y)��(0,0)�ɋ߂Â��Ƃ��̋Ɍ��l�ׂ�D
(x,y)��(0,0)�̋�����r�Ƃ�����
x=r cos��, y=r sin�� f(x,y)==2cos2�� (1) ��=0�̂Ƃ��iy=0, x=t�̂Ƃ��jf(x,y)→2 (2) ��=�̂Ƃ��iy=x=t�̂Ƃ��jf(x,y)→1 (3) ��=�̂Ƃ��ix=0, y=t�̂Ƃ��jf(x,y)→0  �ƂȂ邩��C�i�߂Â����̊p�x���ɂ���ċɌ����ς��̂Łj
�ƂȂ邩��C�i�߂Â����̊p�x���ɂ���ċɌ����ς��̂Łj�Ɍ��lf(x,y)�����݂����C f(0,0)�̒l���ǂ̂悤�� ��`����Ă��Ă��C��(x,y)��(0,0)�ɂ����ĕs�A���ƂȂ�܂��D
����17�N�x�Z�p�m��ꎟ�������m���ʖ��n
�y���w�z�V-8 �@���̂Q�ϐ���f(x,y)�ɑ��āCf(0,0)=0�ƒ�`����D���̂Ƃ��C�_(0,0)�ŘA���ƂȂ�Ȃ����̂͂ǂꂩ�D 1f(x,y)= 2f(x,y)= 3f(x,y)= 4f(x,y)= 5f(x,y)= HELP
(x,y)��(0,0)�̋�����r�Ƃ�����
x=r cos��, y=r sin�� 1 f(x,y)==sin��cos��=sin2�� �͋߂Â��p�x���ɂ���Č��ʂ��ς��̂ŁCr→0�̂Ƃ��Ɍ��l�͑��݂��Ȃ��D���������āC�s�A�� 2 f(x,y)==r cos2��sin��→0 (r→0�̂Ƃ�) �Ɍ��l�Ɗ��l����v���邩��A�� 3 f(x,y)==r cos��sin2��→0 (r→0�̂Ƃ�) �Ɍ��l�Ɗ��l����v���邩��A�� 4 f(x,y)==r cos��(cos2��−sin2��)→0 (r→0�̂Ƃ�) �Ɍ��l�Ɗ��l����v���邩��A�� 5 f(x,y)==r sin��(cos2��−sin2��)→0 (r→0�̂Ƃ�) �Ɍ��l�Ɗ��l����v���邩��A�� |
|||||||||||
|
(x,y)��(0,0)�̋�����r�Ƃ�����
x=r cos��, y=r sin�� =× =×=1×0=0(r→0�̂Ƃ�) → 1 |
(x,y)��(0,0)�̋�����r�Ƃ�����
x=r cos��, y=r sin�� === → (r→0�̂Ƃ�) |

 �@�F
�@�F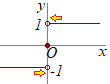 �i��1�j������Ɍ��l�ƉE�Ɍ��l����v���Ȃ��F�Ɍ��l�����݂��Ȃ����Ƃ�����
�i��1�j������Ɍ��l�ƉE�Ɍ��l����v���Ȃ��F�Ɍ��l�����݂��Ȃ����Ƃ�����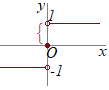 �i��2�j������������O���t�ɒi��������ΘA���ɂȂ�Ȃ�
�i��2�j������������O���t�ɒi��������ΘA���ɂȂ�Ȃ�