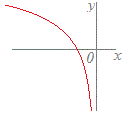|
■逆関数 【はじめに】 (1) 関数と関数でないものの違い
 「定義域の各々の実数xの値に対して,実数yの値が,1つ,しかも唯1つだけ定まる対応関係があるとき,この対応f:x→yを関数といい,y=f(x)などと表します. 「定義域の各々の実数xの値に対して,実数yの値が,1つ,しかも唯1つだけ定まる対応関係があるとき,この対応f:x→yを関数といい,y=f(x)などと表します.
1つのxの値に対して,2つ以上のyの値が対応するような場合(多価関数)は,この頁では関数に含めません.だから,関数と呼ばれるものでは1対多対応のようなものは考えず,1つのxの値に対しては,1つのyだけが対応するものを考えます.
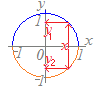
厳密に言えば,あるxの値に対して,対応するyの値が「ない場合=0個の場合」も関数の定義に合わないことになりますが,定義域を絞ることにより,各々のxに対して唯1つのyができる場合は,関数として扱います.例えば,上図のような円のグラフは1つの関数y=f(x)の形には表せず,y=±というように2つの関数で表します.(青で示した上半円がy=,オレンジで示した下半分がy=−)
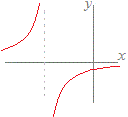
例えば,y=は,x<0のとき対応する実数yがないので,すべての実数xに対しては関数とは言えませんが,定義域をx≧0とかx>1とすると,実数yが唯1つ定まるので,その定義域では関数になります.
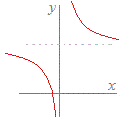
また,y=は,x=1のとき定義されないので すべての実数xに対しては関数とは言えませんが,定義域をx≠1とすると,実数yが唯1つ定まるので,その定義域では関数になります. このように,関数といえるためには,対応するyの値は1個でなければなりませんが,0個(ない)となる部分があるときは,その関数が定義される(1つは対応する値がある)範囲で考える(定義域を絞る)ことにします.
【要点】
 |
[簡単チェック問題1]
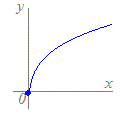
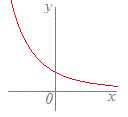
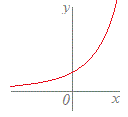
次のグラフ(青色)で表される対応f:x→yのうちで関数とはいえないものを選んでください(番号をクリック).なお,関数が定義されないxの値の範囲を除外すれば,関数とみなせるものは,関数に含めてください. 1 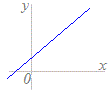 2
2 3 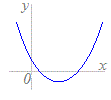 4
4
HELP
4のグラフは,1つのxに対して2つのyが対応しており,関数とはいえません.(2は定義域を0≦x≦1とすれば,各々のxに対して唯1つのyが対応します.)
[簡単チェック問題2]
次のグラフ(青色)で表される対応f:x→yのうちで関数とはいえないものを選んでください(番号をクリック).なお,関数が定義されないxの値の範囲を除外すれば,関数とみなせるものは,関数に含めてください. 1  2
2 3  4
4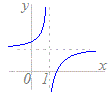
HELP
2のグラフは,1つのxに対して3つ(あるいは2つ)のyが対応しているところがあり,関数とはいえません.(1は,1つのyに3つ(あるいは2つのxが対応するところがありますが,これは関数の定義には影響しません.3, 4は定義域をx≠1とすれば,各々のxに対して唯1つのyが対応します.)
|
|
(2) 1対1の関数
関数のうちで,異なるxには異なるyが対応しているものを,1対1の関数といいます.
「1対1の関数」 ⇔ 「x1≠x2 → f(x1)≠f(x2)」
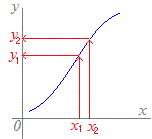
「x1=x2 ← f(x1)=f(x2)」
あるいは 「x1=x2 ← y1=y2」 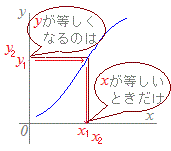 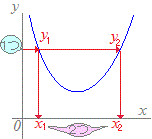
【要点】
1対1の関数であるかどうかを
○ 式で調べるには 「y1=y2 → x1=x2」のとき1対1といえる ○ 連続関数について,グラフで調べるには 「単調増加」または「単調減少」のとき,1対1といえる ※ 1対1の関数であるかどうかは,各々のyに対するxの個数の性質
◎すべてのyに対してxは1個→1対1
○あるyに対してxは0個(なし)→値域に属するyだけを考えればよいことにすると,この場合は考えなくてもよい ○あるyに対してxが2個(またはそれ以上)→1対1でない
1
y=2x−1よりx=だから
2「y1=y2 → x1=x2」(yが等しければxも等しい)といえる →1対1
y=よりx=−1+だから
「y1=y2 → x1=x2」(yが等しければxも等しい)といえる →1対1  3
3
y=x2−1よりx=±(2つある)から
「y1=y2 → x1=x2」(yが等しければxも等しい)とはいえない →1対1ではない 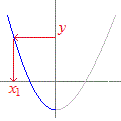 4
4
y=x2−1 (x≦0)よりx=−(1つに決まる)から
「y1=y2 → x1=x2」(yが等しければxも等しい)といえる →1対1 |
《参考》
連続な関数で1対1の関数となるのは,単調増加関数と単調減少関数だけ 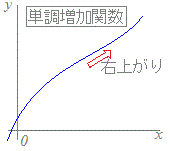  ⇒次のようなものは1対1の関数ではない  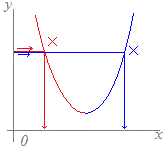 
4は増加の区間と減少の区間があり,1対1ではない.
|
|
《ここまでのまとめ》
○ 「関数である」ことによって,どのxにも,1つのyが対応することになります.  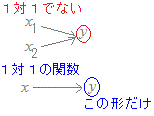 |
○ 「1対1の関数」であれば,yからxへの「逆向きの対応」を唯1通りに定めることができます.
 もし,元の関数が1対1の関数でなければ,逆向きの対応を考えようとすると,1つのyに対して,2つ(またはそれ以上の)xがあることになり,逆向きの対応が関数ではなくなります.
もし,元の関数が1対1の関数でなければ,逆向きの対応を考えようとすると,1つのyに対して,2つ(またはそれ以上の)xがあることになり,逆向きの対応が関数ではなくなります.
1対1の関数であるかどうかを
○ 式で調べる:「y1=y2 → x1=x2」 ○ (連続関数の場合に)グラフで調べる:「単調増加」または「単調減少」 |
|
(3) 定義域と値域
関数y=f(x)が定義されるxの値の範囲を定義域といいます.また,独立変数xが定義域のすべての値をとって変化するとき,従属変数yの取り得る値の範囲を値域といいます.  【例】
【例】y=f(x)=x2−2x (x≧1)のとき, xの値の範囲を指定しているx≧1が定義域です. このとき,y=f(x)=(−1)x2−1となることに注意すると,右図のグラフの青で示した部分になり,yの値の範囲はy≧−1となり,これが値域です. この同じ関数y=f(x)=x2−2xでも,定義域をx≦0とすると,値域はy≧0になります.
【例】
上記の関数y=f(x)=x2−2xについて 定義域をx≧1とすれば,1対1の関数となります. 定義域をx≧2, x≧3, x≧4, ...あるいはx≦1, x≦0, x≦−1, ...としても1対1の関数となりますが,定義域をx≧0, −1≦x, 0≦x≦2などとすると1対1の関数にはなりません.また,定義域を指定しない場合(これは−∞<x<∞の略と解される)も1対1の関数にはなりません.上のグラフを見ると,谷の右側か左側(の一部)だけからなる区間を定義域とすると1対1の関数になることがわかります. |
 右図の青線で示したグラフになるから,
右図の青線で示したグラフになるから,2
[簡単チェック問題6]
次うちで1対1の関数でないものを選んでください(番号をクリック). 1y=(x−1)2+2 (x≦0) 2y= (x≧0) 3y= (x≦1) 4y= (−1≦x≦1) HELP  各々,右図の青線で示したグラフになり,4だけは単調減少関数でなく,増加の区間と減少の区間がある
各々,右図の青線で示したグラフになり,4だけは単調減少関数でなく,増加の区間と減少の区間がある |
|
(1) 逆関数の定義
 関数y=f(x)によって,xの値にyの値が対応しているときに,その逆の対応をf(x)の逆関数といいy=f−1(x)で表します. 関数y=f(x)によって,xの値にyの値が対応しているときに,その逆の対応をf(x)の逆関数といいy=f−1(x)で表します.
【例】
y=f(x)=2xのとき, これに対する逆の対応はx= となります.対応関係としてはこれでもわかります(2を掛けるという操作の逆は,2で割るということ)が, 「通常,独立変数をxで表し,従属変数をyで表す習慣に従って、文字を入れ替えて」 y=f−1(x)=を逆関数とします. ○ 上の解説で,関数y=f(x)に対して逆関数が定義されるためには,元の関数の段階でyからxへの対応が唯1通りに定まらなければなりません.したがって,元の関数y=f(x)が1対1の関数である場合だけ,逆関数が定義できるということになります. 
【例】
元の関数,定義域,値域がf(x)=x2 (x≧2, y≧4)のとき (*) 準備:f(x)をyとする y=x2 (x≧2, y≧4)
(1) 文字xとyを入れ替えると,その文字に付着してる値の範囲,すなわち,定義域と値域も入れ替わります.
(*) 後始末:yをf−1(x)とする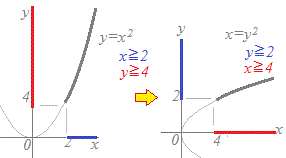 y2=x (y≧2, x≧4) y=± (y≧2, x≧4) y≧2>0により y= (y≧2, x≧4) f−1(x)= (y≧2, x≧4) ※ 逆関数を求める手順は,「逆に解くこと」と「習慣に従って文字を入れ替えること」の2つから成り立っています.どちらを先に行っても同じ結果が出ますが,「定義域」や「値域」も考えるときは,先に文字を入れ替える方がわかりやすいようです.
【逆関数の求め方(まとめ)】
 ○ 逆関数の定義域と値域は,元の関数の定義域と値域を入れ替えたものになる. |
[例題1]
(解説)f(x)=−x+3の逆関数f−1(x)を求めてください. (*) 準備:f(x)をyとする y=−x+3 (1) 文字xとyを入れ替える. x=−y+3 (2) yについて解く. 4x=−3y+12 3y=−4x+12 y=−x+4 (*) 後始末:yをf−1(x)とする f−1(x)=−x+4
[例題2]
(解説)f(x)=1− (1≦x≦9)の逆関数f−1(x)を求めてください. 元の関数,定義域,値域は f(x)=1− (1≦x≦9, −2≦f(x)≦0) (*) 準備:f(x)をyとする y=1− (1≦x≦9, −2≦y≦0) (1) 文字xとyを入れ替える.そのとき,定義域と値域も入れ替える. x=1− (1≦y≦9, −2≦x≦0) (2) yについて解く. =1−x (1≦y≦9, −2≦x≦0) y=(1−x)2=(x−1)2 (1≦y≦9, −2≦x≦0) (*) 後始末:yをf−1(x)とする f−1(x)=(1−x)2=(x−1)2 (−2≦x≦0)
[例題3]
f(x)=x2+2x−1 (x≦−2)の逆関数f−1(x)を求めてください.  (解説)
(解説)元の関数,定義域は f(x)=x2+2x−1 (x≦−2) f(x)をyとする y=x2+2x−2=(x+1)2−2 (x≦−2) 右図のように,頂点の左側の区間になるから y=(x+1)2−2 (x≦−2, y≧−1) 文字xとyを入れ替える. x=(y+1)2−2 (y≦−2, x≧−1) yについて解く. (y+1)2=x+2 (y≦−2, x≧−1) y+1=± (y≦−2, x≧−1) y=−1± (y≦−2, x≧−1) …(*) y≦−2<(−1)だから y=−1− (y≦−2, x≧−1) yをf−1(x)で表すと f−1(x)=−1− (x≧−1)
(*) の部分は,y2+2y−2=xより,「解の公式を用いて解く」と考えると,もっと多くの問題に対応できる.
y2+2y−(x+2)=0 y=−1±
[例題4]
f(x)= (x≧0)の逆関数f−1(x)を求めてください. 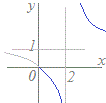 (解説)
(解説)f(x)をyで表すと y==1+ 右図のように漸近線がx=2, y=1の直角双曲線になる.(x≧0の区間のうち,実際にはx=2では定義されない) 定義域は0≦x<2, 2<x 値域はy≦0, 1<y 文字xとyを入れ替える. x= (0≦y<2, 2<y, x≦0, 1<x) yについて解く. yx−2x=y (0≦y<2, 2<y, x≦0, 1<x) (x−1)y=2x (0≦y<2, 2<y, x≦0, 1<x) y= (0≦y<2, 2<y, x≦0, 1<x) したがって f−1(x)= (x≦0, 1<x) |
|
f(x)をyとする
y=2x+1 文字xとyを入れ替える. x=2y+1 yについて解く. 2y=x−1 y= yをf−1(x)で表すと f−1(x)= →1
|
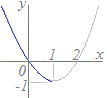 f(x)をyとする.
f(x)をyとする.y=x2−2x=(x−1)2−1 グラフは右図のようになるから,定義域がx≦1のとき,値域はy≧−1 文字xとyを入れ替える. x=y2−2y (y≦1, x≧−1) yについて解く. y2−2y−x=0より,解の公式を用いると y=1± (y≦1, x≧−1) ここで,y≦1だから y=1− (y≦1, x≧−1) yをf−1(x)で表すと f−1(x)=1− (x≧−1) →4
|
|
[問題3]
f(x)=ex−1+2 (x≧1)の逆関数f−1(x)とその定義域,値域を求めてください. 12+log(x−1) (x≧3, y≧1) 22+log(x−1) (x≧1, y≧3) 31+log(x−2) (x≧3, y≧1) 41+log(x−2) (x≧1, y≧3) HELP
f(x)をyとする
y=ex−1+2 (x≧1, y≧3) 文字xとyを入れ替える. x=ey−1+2 (y≧1, x≧3) yについて解く. ey−1=x−2 (y≧1, x≧3) y−1=log(x−2) (y≧1, x≧3) y=1+log(x−2) (y≧1, x≧3) yをf−1(x)で表すと f−1(x)=1+log(x−2) (x≧3, y≧1) →3
|
 f(x)をyとする.
f(x)をyとする.y= (x≧0) グラフは右図のようになるから,定義域がx≧0のとき,値域は−1≦y<2
グラフを使わずに,数式変形だけで値域を求めたいときは,次の分数不等式を解く.
文字xとyを入れ替える.y= (x≧0) x=−≧0 一般に,分数不等式 ≦0の解は f(x)g(x)≦0, g(x)≠0を解けば得られるから ≦0より −1≦y<2 x= (y≧0, −1≦x<2) yについて解く. xy+x=2y−1 (y≧0, −1≦x<2) (x−2)y=−(x+1) (y≧0, −1≦x<2) y=− (y≧0, −1≦x<2) yをf−1(x)で表すと f−1(x)=− (−1≦x<2) →4
|
|
(2) 逆関数の性質
(1) ある関数f(x)とその逆関数f−1(x)のグラフとは,y=xの直線に関して対称に折り曲げたものになる.
(解説)(2) ある関数f(x)とその逆関数f−1(x)のグラフとは,増加,減少が一致する. (1) y=xということにこだわり過ぎると難しく見えますが,次のように簡単な話です. 逆関数を求めるときに,文字xとyを入れ替えますが,このときに縦と横が逆になります.だから,45°の線を折り目として折り返したものになります.(なお,方程式を逆に解く変形をしても,グラフには何も影響なく,全く同じグラフです.グラフが変わるのは,文字を入れ替えたためです.)  関数f(x)について,xが増えればyが増えるとき,その逆関数f−1(x)ではyが増えればxが増えることになり,増加関数⇒増加関数となります.減少関数のときも同様です. |
y=xの直線に関して対称に折り曲げるとわかります.
 →1
y=xの直線に関して対称に折り曲げるとわかります.
 →2
|