|
【はじめに】 (1) 関数と関数でないものの違い
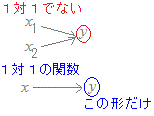
 「定義域の各々の実数xの値に対して,実数yの値が,1つ,しかも唯1つだけ定まる対応関係があるとき,この対応f:x→yを関数といい,y=f(x)などと表します. 「定義域の各々の実数xの値に対して,実数yの値が,1つ,しかも唯1つだけ定まる対応関係があるとき,この対応f:x→yを関数といい,y=f(x)などと表します.
1つのxの値に対して,2つ以上のyの値が対応するような場合(多価関数)は,この頁では関数に含めません.だから,関数と呼ばれるものでは1対多対応のようなものは考えず,1つのxの値に対しては,1つのyだけが対応するものを考えます.
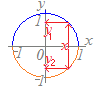
厳密に言えば,あるxの値に対して,対応するyの値が「ない場合=0個の場合」も関数の定義に合わないことになりますが,定義域を絞ることにより,各々のxに対して唯1つのyができる場合は,関数として扱います.例えば,上図のような円のグラフは1つの関数y=f(x)の形には表せず,y=±というように2つの関数で表します.(青で示した上半円がy=,オレンジで示した下半分がy=−)
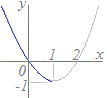
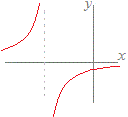
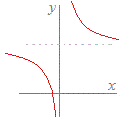
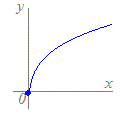
例えば,y=は,x<0のとき対応する実数yがないので,すべての実数xに対しては関数とは言えませんが,定義域をx≧0とかx>1とすると,実数yが唯1つ定まるので,その定義域では関数になります.
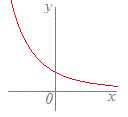
また,y=は,x=1のとき定義されないので すべての実数xに対しては関数とは言えませんが,定義域をx≠1とすると,実数yが唯1つ定まるので,その定義域では関数になります. このように,関数といえるためには,対応するyの値は1個でなければなりませんが,0個(ない)となる部分があるときは,その関数が定義される(1つは対応する値がある)範囲で考える(定義域を絞る)ことにします.
【要点】
 |
|
[簡単チェック問題1]
次のグラフ(青色)で表される対応f:x→yのうちで関数とはいえないものを選んでください(番号をクリック).なお,関数が定義されないxの値の範囲を除外すれば,関数とみなせるものは,関数に含めてください. 1 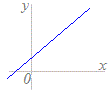 2
2 3 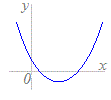 4
4
解説
4のグラフは,1つのxに対して2つのyが対応しており,関数とはいえません.(2は定義域を0≦x≦1とすれば,各々のxに対して唯1つのyが対応します.)
[簡単チェック問題2]
次のグラフ(青色)で表される対応f:x→yのうちで関数とはいえないものを選んでください(番号をクリック).なお,関数が定義されないxの値の範囲を除外すれば,関数とみなせるものは,関数に含めてください. 1  2
2 3  4
4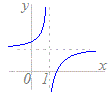
解説
2のグラフは,1つのxに対して3つ(あるいは2つ)のyが対応しているところがあり,関数とはいえません.(1は,1つのyに3つ(あるいは2つのxが対応するところがありますが,これは関数の定義には影響しません.3, 4は定義域をx≠1とすれば,各々のxに対して唯1つのyが対応します.)
|
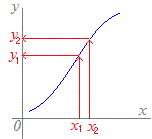
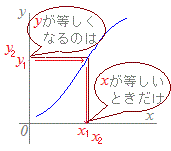








 【例】
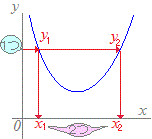
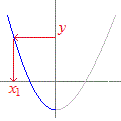
【例】 右図の青線で示したグラフになるから,
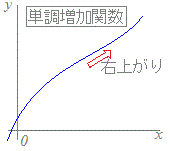
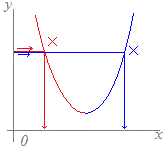
右図の青線で示したグラフになるから, 各々,右図の青線で示したグラフになり,
各々,右図の青線で示したグラフになり, 関数
関数
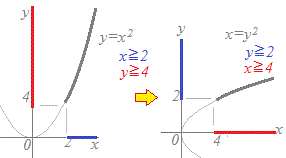

 (解説)
(解説)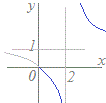 (解説)
(解説)