(3.4)����������
 \( \displaystyle \frac{d^2y}{dx^2}-3\frac{dy}{dx}+2y=2\cos x \) \( \displaystyle \frac{d^2y}{dx^2}-3\frac{dy}{dx}+2y=2\cos x \)
�@��������
=y\apos(0)=1&chf=bg,s,ffffdd) \( \displaystyle y(0)=y'(0)=1 \) \( \displaystyle y(0)=y'(0)=1 \)
����  \( \displaystyle x \) \( \displaystyle x \)�̊�
 \( \displaystyle y \) \( \displaystyle y \)�����߂Ă��������D
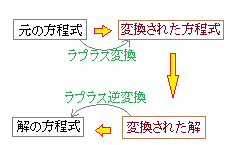
��A:���v���X�ϊ��ɂ���������
�@���ӂ����v���X�ϊ�����
-sy(0)-y\apos(0)-3(s\mathcal{L}(y)-y(0))%2B 2\mathcal{L}(y)) \( \displaystyle s^2\mathcal{L}(y)-sy(0)-y'(0)-3(s\mathcal{L}(y)-y(0))+ 2\mathcal{L}(y) \) \( \displaystyle s^2\mathcal{L}(y)-sy(0)-y'(0)-3(s\mathcal{L}(y)-y(0))+ 2\mathcal{L}(y) \)
 \( \displaystyle =2\frac{s}{s^2+1} \) \( \displaystyle =2\frac{s}{s^2+1} \)
���������������
-s-1-3(s\mathcal{L}(y)-1)%2B 2\mathcal{L}(y)=\frac{2s}{s^2%2B 1}) \( \displaystyle s^2\mathcal{L}(y)-s-1-3(s\mathcal{L}(y)-1)+ 2\mathcal{L}(y)=\frac{2s}{s^2+ 1} \) \( \displaystyle s^2\mathcal{L}(y)-s-1-3(s\mathcal{L}(y)-1)+ 2\mathcal{L}(y)=\frac{2s}{s^2+ 1} \)
\mathcal{L}(y)=\frac{2s}{s^2%2B 1}%2B s-2) \( \displaystyle (s^2-3s+ 2)\mathcal{L}(y)=\frac{2s}{s^2+ 1}+ s-2 \) \( \displaystyle (s^2-3s+ 2)\mathcal{L}(y)=\frac{2s}{s^2+ 1}+ s-2 \)
(s-2)\mathcal{L}(y)=\frac{2s}{s^2%2B 1}%2B s-2) \( \displaystyle (s-1)(s-2)\mathcal{L}(y)=\frac{2s}{s^2+ 1}+ s-2 \) \( \displaystyle (s-1)(s-2)\mathcal{L}(y)=\frac{2s}{s^2+ 1}+ s-2 \)
=\frac{2s}{(s^2%2B 1)(s-1)(s-2)}%2B\frac{1}{s-1}) \( \displaystyle \mathcal{L}(y)=\frac{2s}{(s^2+ 1)(s-1)(s-2)}+\frac{1}{s-1} \) \( \displaystyle \mathcal{L}(y)=\frac{2s}{(s^2+ 1)(s-1)(s-2)}+\frac{1}{s-1} \)
�E�ӂ������ɕ�������D
(s-1)(s-2)}=\frac{as%2B b}{s^2%2B 1}%2B\frac{c}{s-1}%2B\frac{d}{s-2}&chco=aa4422) \( \displaystyle \frac{2s}{(s^2+ 1)(s-1)(s-2)}=\frac{as+ b}{s^2+ 1}+\frac{c}{s-1}+\frac{d}{s-2} \) \( \displaystyle \frac{2s}{(s^2+ 1)(s-1)(s-2)}=\frac{as+ b}{s^2+ 1}+\frac{c}{s-1}+\frac{d}{s-2} \)
�Ƃ����āC���ӂ̌W�����r�����
3���F  \( \displaystyle a+ c+ d=0 \) \( \displaystyle a+ c+ d=0 \)
2���F  \( \displaystyle -3a+ b-2c-d=0 \) \( \displaystyle -3a+ b-2c-d=0 \)
1���F  \( \displaystyle 2a-3b+ c+ d=2 \) \( \displaystyle 2a-3b+ c+ d=2 \)
�萔���F  \( \displaystyle 2b-2c-d=0 \) \( \displaystyle 2b-2c-d=0 \)
���̘A����������������
 \( \displaystyle a=\frac{1}{5},\hspace{3px}b=-\frac{3}{5},\hspace{3px}c=-1,\hspace{3px}d=\frac{4}{5} \) \( \displaystyle a=\frac{1}{5},\hspace{3px}b=-\frac{3}{5},\hspace{3px}c=-1,\hspace{3px}d=\frac{4}{5} \)
=\frac{\frac{1}{5}s-\frac{3}{5}}{s^2%2B 1}-\frac{1}{s-1}%2B\frac{4}{5}\cdot\frac{1}{s-2}%2B\frac{1}{s-1}) \( \displaystyle \mathcal{L}(y)=\frac{\dfrac{1}{5}s-\dfrac{3}{5}}{s^2+ 1}-\frac{1}{s-1}+\frac{4}{5}\cdot\frac{1}{s-2}+\frac{1}{s-1} \) \( \displaystyle \mathcal{L}(y)=\frac{\dfrac{1}{5}s-\dfrac{3}{5}}{s^2+ 1}-\frac{1}{s-1}+\frac{4}{5}\cdot\frac{1}{s-2}+\frac{1}{s-1} \)
 \( \displaystyle =\frac{1}{5}\cdot\frac{s}{s^2+ 1}-\frac{3}{5}\cdot\frac{1}{s^2+ 1}+\frac{4}{5}\cdot\frac{1}{s-2} \) \( \displaystyle =\frac{1}{5}\cdot\frac{s}{s^2+ 1}-\frac{3}{5}\cdot\frac{1}{s^2+ 1}+\frac{4}{5}\cdot\frac{1}{s-2} \)
 \( \displaystyle y=\frac{1}{5}\cos x-\frac{3}{5}\sin x+\frac{4}{5}e^{2x} \)
…�i���j \( \displaystyle y=\frac{1}{5}\cos x-\frac{3}{5}\sin x+\frac{4}{5}e^{2x} \)
…�i���j
��B:2�K���`�����������̕M�Z�ɂ���������
�������� &chco=aa4422) \( \displaystyle y''+ ay'+ by=R(x) \) \( \displaystyle y''+ ay'+ by=R(x) \)�̓�����ɁC
����������  \( \displaystyle y''+ ay'+ by=0 \) \( \displaystyle y''+ ay'+ by=0 \)�̈�ʉ����������
�������� &chco=aa4422) \( \displaystyle y''+ ay'+ by=R(x) \) \( \displaystyle y''+ ay'+ by=R(x) \)�̈�ʉ���������
|
�������� \( \displaystyle y''-3y'+2y=2\cos x \)�̂P�̓�����́C \( \displaystyle y''-3y'+2y=2\cos x \)�̂P�̓�����́C
 \( \displaystyle y=-\frac{3}{5}\sin x+\frac{1}{5}\cos x \) \( \displaystyle y=-\frac{3}{5}\sin x+\frac{1}{5}\cos x \)
�i \( \displaystyle y=A\sin x+ B\cos x \)�Ƃ����āC \( \displaystyle y=A\sin x+ B\cos x \)�Ƃ����āC \( \displaystyle y''-3y'+ 2y=2\cos x \)�ƂȂ�A, B�����߂���悢�j \( \displaystyle y''-3y'+ 2y=2\cos x \)�ƂȂ�A, B�����߂���悢�j
����������
 \( \displaystyle y''-3y'+ 2y=0 \) \( \displaystyle y''-3y'+ 2y=0 \)
�̓��������� \( \displaystyle r^2-3r+ 2=0 \)�͈قȂ�2�̎����� \( \displaystyle r^2-3r+ 2=0 \)�͈قȂ�2�̎�����
 \( \displaystyle r=1,\hspace{2px}2 \)��������C�����������̈�ʉ��� \( \displaystyle r=1,\hspace{2px}2 \)��������C�����������̈�ʉ���
 \( \displaystyle C_1e^x+ C_2e^{2x} \) \( \displaystyle C_1e^x+ C_2e^{2x} \)
���̔����������̈�ʉ���
 \( \displaystyle y=C_1e^x+ C_2e^{2x}-\frac{3}{5}\sin x+\frac{1}{5}\cos x \) \( \displaystyle y=C_1e^x+ C_2e^{2x}-\frac{3}{5}\sin x+\frac{1}{5}\cos x \)
=y\apos(0)=1) \( \displaystyle y(0)=y'(0)=1 \)�ɂ�� \( \displaystyle y(0)=y'(0)=1 \)�ɂ��
 \( \displaystyle C_1=0,\hspace{3px}C_2=\frac{4}{5} \) \( \displaystyle C_1=0,\hspace{3px}C_2=\frac{4}{5} \)
 \( \displaystyle y=\frac{4}{5}e^{2x}-\frac{3}{5}\sin x+\frac{1}{5}\cos x \)
…�i���j \( \displaystyle y=\frac{4}{5}e^{2x}-\frac{3}{5}\sin x+\frac{1}{5}\cos x \)
…�i���j
��C:�t���[�\�t�gwxMaxima�ɂ���������
�@���j���[�����ǂ��āC�u�������v→�u�����������������v
siki1:ode2('diff(y,x,2)-3*'diff(y,x,1)+2*y
=2*cos(x), y, x);
�̂悤�ɕ������ɖ��O��t���Ă���
��2�K������\������ɂ́C'diff(y,x, 2)�Ƃ���Ƃ悢
 \( \displaystyle y=-\frac{3\sin x-\cos x}{5}+ \%k1 \%e^{2x}+ \%k2\%e^{x} \) \( \displaystyle y=-\frac{3\sin x-\cos x}{5}+ \%k1 \%e^{2x}+ \%k2\%e^{x} \)
�Ƃ����`�ň�ʉ���������
ic2( siki1,x=0,y=1,'diff(y,x)=1);
�Ƃ����`�ŏ�������������
�i�Q�K�����������ŏ��������ɑΉ��������������߂�ɂ́c initial value problems for 2nd order differential equations���ic2( )�����g����Dy'=1�Ƃ��������́C'diff(y,x)=1�ŏ�������擪�̃A�|�X�g���t�B�[�ɒ��Ӂj
 \( \displaystyle y=\frac{4}{5}e^{2x}-\frac{3}{5}\sin x+\frac{1}{5}\cos x \)
…�i���j \( \displaystyle y=\frac{4}{5}e^{2x}-\frac{3}{5}\sin x+\frac{1}{5}\cos x \)
…�i���j
|