平方数の逆数の和

大きな区分

現在地と前後の項目（サブメニュー）

数列,関数の極限
合成関数
逆関数
逆三角関数
双曲線関数
関数の連続性
εδ論法
フーリエ係数,自然数の累乗の逆数の和

無限級数
収束半径，テイラー展開，マクローリン展開
テイラーの定理，マクローリンの定理
マクローリン展開
逆三角関数の微分法
偏微分
2変数関数の極値,ラグランジュの未定乗数法
ラプラス変換の基本
連分数
ガンマ関数,ベータ関数
ベクトル解析の公式

→ 携帯版は別頁

== 自然数の累乗の逆数の和 ==

（リーマンのゼータ関数，バーゼル問題，フーリエ級数）

　このページでは，次のような級数の和を扱う．
（その内容が書かれた場所に直接ジャンプするには，太字青の記号をクリック）

$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots=\infty$ …①
$1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots=\frac{\pi}{4}$ …②
$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots=\log 2$ …(*1)

$1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots=\frac{\pi^2}{6}$ …③
$1-\frac{1}{2^2}+\frac{1}{3^2}-\frac{1}{4^2}+\cdots=\frac{\pi^2}{12}$ …④
$1+\frac{1}{3^2}+\frac{1}{5^2}+\frac{1}{7^2}+\cdots=\frac{\pi^2}{8}$ …⑤
$\frac{1}{2^2}+\frac{1}{4^2}+\frac{1}{6^2}+\frac{1}{8^2}+\cdots=\frac{\pi^2}{24}$ …⑥

$1+\frac{1}{2^3}+\frac{1}{3^3}+\frac{1}{4^3}+\cdots=?$ …⑦
$1-\frac{1}{3^3}+\frac{1}{5^3}-\frac{1}{7^3}+\cdots=\frac{\pi^3}{32}$ …⑧

$1+\frac{1}{2^4}+\frac{1}{3^4}+\frac{1}{4^4}+\cdots=\frac{\pi^4}{90}$ …⑨
$1-\frac{1}{2^4}+\frac{1}{3^4}-\frac{1}{4^4}+\cdots=\frac{7}{720}\pi^4$ …⑩

　これらを求めるために，次のフーリエ級数展開を利用する．

$x=-2\sum_{n=1}^{\infty}\frac{\cos n\pi}{n}\sin nx$ …[1]

鋸歯状波（三角波）

$|x|=\frac{\pi}{2}+\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{\cos n\pi-1}{n^2}\cos nx$ …[2]

方形波をf(x)とすると

$f(x)=\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{1-\cos n\pi}{n}\sin nx$ …[3]

$x^2=\frac{\pi^2}{3}+ 4\sum_{n=1}^{\infty}\frac{\cos n\pi}{n^2}\cos nx$ …[4]
$x^3=\sum_{n=1}^{\infty}\left(-\frac{2\pi^2\cos n\pi}{n}+\frac{12\cos n\pi}{n^3}\right)\sin nx$ …[5]
$x^4=\frac{\pi^4}{5}+\sum_{n=1}^{\infty}\frac{8}{n^2}\left(\pi^2-\frac{6}{n^2}\right)\cos n\pi\cos nx$ …[6]

（参考１）
これらは，リーマンのゼータ関数
$\zeta(s)=\frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\cdots$
において，sが正の整数であるときの値となっている．
$\zeta(1)=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots$
$\zeta(2)=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots$
$\zeta(4)=\frac{1}{1^4}+\frac{1}{2^4}+\frac{1}{3^4}+\frac{1}{4^4}+\cdots$
（参考２）
　s=１のとき，級数の和（調和級数と呼ばれるもの）が無限大に発散することは，積分を用いて示すことができる．

　図のように， $y=\frac{1}{x}$ のグラフと柱状グラフを重ねて描くと，曲線の下にできる図形の面積よりも柱状図形の面積の方が大きくなります．
$\int_1^2\frac{1}{x}dx\lt 1$
$\int_2^3\frac{1}{x}dx\lt\frac{1}{2}$
$\int_3^4\frac{1}{x}dx\lt\frac{1}{3}\hspace{10}\cdots\hspace{2}\cdots$
$\int_n^{n+ 1}\frac{1}{x}dx\lt\frac{1}{n}$
辺々加えたとき，左辺は1からn+1までの定積分でつながるから
$\int_1^{n+ 1}\frac{1}{x}dx\lt 1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$
$\left[\log x\right]_1^{n+ 1}\lt 1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$
$\log(n+ 1)\lt 1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}$
ここで $n\rightarrow\infty$ の極限をとると
$\lim_{n\rightarrow\infty}\log(n+ 1)=\infty$
だから
$1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}\rightarrow\infty$ →①

　s>1のとき， $y=\frac{1}{x^s}$ のグラフの下に柱状グラフを描くと（0<x<1の部分の1だけは別に加える），有限の積分値よりも級数の和が小さく，級数は単調増加かつ上に有界となって，収束することが言える．

$1+\frac{1}{2^s}+\frac{1}{3^s}+\cdots+\frac{1}{n^s}$
$\lt 1+\int_1^n\frac{1}{x^s}dx$
$=1+\frac{1}{1-s}\left[x^{1-s}\right]_1^n$
$=1+\frac{1}{1-s}(n^{1-s}-1)$
$=1+\frac{1}{1-s}(\frac{1}{n^{s-1}}-1)$
$\rightarrow 1+\frac{1}{1-s}(0-1)$
$=\frac{s}{s-1}$
例えばs=2のとき
$1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots+\frac{1}{n^2}+\cdots\lt 2$
s=3のとき
$1+\frac{1}{2^3}+\frac{1}{3^3}+\cdots+\frac{1}{n^3}+\cdots\lt\frac{3}{2}$

　s>1のとき，このように収束することが示せるが，具体的にどのような値になるかということは，なかなか難しい.17世紀から18世紀に最初に研究された平方数の逆数の和
$1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots=\frac{\pi^2}{6}$
を求める問題は，これを研究したベルヌーイやオイラーが住んでいたスイスの都市バーゼルの名をとって「バーゼル問題」と呼ばれることがある．
（分数を足しているだけなのに，なぜ $\pi$ が出てくるのか，とても不思議な結果になっており興味を持ってもらえるかもしれない）

１．三角関数の定積分（復習）

まず，三角関数の定積分について，次の式を確認しておきます．（m, nは正の整数）
$\int_{-\pi}^{\pi}kdx$ $=\left[kx\right]_{-\pi}^{\pi}$ $=2k\pi$ …(1.1)
$\int_{-\pi}^{\pi}\sin nxdx$ $=\left[-\frac{\cos nx}{n}\right]_{-\pi}^{\pi}$ $=0$ …(1.2)
$\int_{-\pi}^{\pi}\cos nxdx$ $=\left[\frac{\sin nx}{n}\right]_{-\pi}^{\pi}$ $=0$ …(1.3)

m≠nのとき
$\int_{-\pi}^{\pi}\cos mx\sin nxdx=0$ …(2.1)
$=\frac{1}{2}\int_{-\pi}^{\pi}\{\sin(m+ n)x-\sin(m-n)x\}dx=0$

←(1.2)から言える

m=nのとき
$\int_{-\pi}^{\pi}\cos mx\sin nxdx=0$ …(2.2)
$=\frac{1}{2}\int_{-\pi}^{\pi}\{\sin 2mx-0\}dx=0$

←(1.2)から言える

m≠nのとき
$\int_{-\pi}^{\pi}\cos mx\cos nxdx=0$ …(2.3)
$=\frac{1}{2}\int_{-\pi}^{\pi}\{\cos(m+ n)x+\cos(m-n)x\}dx=0$

←(1.3)から言える

m=nのとき
$\int_{-\pi}^{\pi}\cos mx\cos nxdx=\pi$ …(2.4)
$=\frac{1}{2}\int_{-\pi}^{\pi}\{\cos 2mx+ 1\}dx=\frac{1}{2}\left[0+ x\right]_{-\pi}^{\pi}=\pi$

m≠nのとき
$\int_{-\pi}^{\pi}\sin mx\sin nxdx=0$ …(2.5)
$=\frac{1}{2}\int_{-\pi}^{\pi}\{\cos(m-n)x-\cos(m+ n)x\}dx=0$

←(1.3)から言える

m=nのとき
$\int_{-\pi}^{\pi}\sin mx\sin nxdx=\pi$ …(2.6)
$=\frac{1}{2}\int_{-\pi}^{\pi}\{1-\cos 2nx\}dx=\frac{1}{2}\left[x-0\right]_{-\pi}^{\pi}=\pi$

【まとめ】
$\int_{-\pi}^{\pi}\cos mx\sin nxdx=0$ …(3.1)
m≠nのとき
$\int_{-\pi}^{\pi}\cos mx\cos nxdx=0$ …(3.2)
$\int_{-\pi}^{\pi}\sin mx\sin nxdx=0$ …(3.3)
m=nのとき
$\int_{-\pi}^{\pi}\cos mx\cos nxdx=\pi$ …(3.4)
$\int_{-\pi}^{\pi}\sin mx\sin nxdx=\pi$ …(3.5)

※覚え方は簡単：同じ関数の組合せ（次の図の対角成分）だけ残る．他は全部０

	cos x	cos 2x	cos 3x	…	sin x	sin 2x	sin 3x
cos x	π	0	0	0	0	0	0	0
cos 2x	0	π	0	0	0	0	0	0
cos 3x	0	0	π	0	0	0	0	0
…	0	0	0	…	0	0	0	0
sin x	0	0	0	0	π	0	0	0
sin 2x	0	0	0	0	0	π	0	0
sin 3x	0	0	0	0	0	0	π	0
…	0	0	0	0	0	0	0	…

２．フーリエ係数の公式

$f(x)=\frac{a_0}{2}+ (a_1\cos x+ b_1\sin x)+(a_2\cos 2x+ b_2\sin 2x)\cdots$
$=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos nx+ b_n\sin nx)$
のとき
$a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx$ …(4.1)
$a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nxdx$ …(4.2)
$b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nxdx$ …(4.3)

（証明）
(4.1)←
$f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos nx+ b_n\sin nx)$
の両辺を $-\pi\underline{\le}x\underline{\le}\pi$ の区間で積分すると
（左辺）= $\int_{-\pi}^{\pi}f(x)dx$

（右辺）=
$\int_{-\pi}^{\pi}\frac{a_0}{2}dx+\sum_{n=1}^{\infty}\{a_n\int_{-\pi}^{\pi}\cos nxdx+ b_n\int_{-\pi}^{\pi}\sin nxdx\}$
(1.1)により
$\int_{-\pi}^{\pi}\frac{a_0}{2}dx=a_0\pi$
(1.2)により
$\int_{-\pi}^{\pi}\sin nxdx=0$
(1.3)により
$\int_{-\pi}^{\pi}\cos nxdx=0$
だから，（右辺）= $a_0\pi$
これらが等しくなるためには，
$a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx$
※ただし，初めの定義で定数項を $\frac{a_0}{2}$ とおいていることに注意

(4.2)←
$f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos nx+ b_n\sin nx)$
の両辺に $\cos mx$ を掛けて $-\pi\underline{\le}x\underline{\le}\pi$ の区間で積分すると
（左辺）= $\int_{-\pi}^{\pi}f(x)\cos mxdx$
（右辺）= $\int_{-\pi}^{\pi}\frac{a_0}{2}\cos mxdx$
$+\sum_{n=1}^{\infty}\{a_n\int_{-\pi}^{\pi}\cos mx\cos nxdx+ b_n\int_{-\pi}^{\pi}\cos mx\sin nxdx\}$
ここで，(1.3)により
$\int_{-\pi}^{\pi}\frac{a_0}{2}\cos mxdx=0$
(3.2)(3.4)により，m≠nのときは消えるから
$\sum_{n=1}^{\infty}a_n\int_{-\pi}^{\pi}\cos mx\cos nxdx=a_m\pi$
(3.1)により
$\sum_{n=1}^{\infty}b_n\int_{-\pi}^{\pi}\cos mx\sin nxdx=0$
以上から，（右辺）= $a_m\pi$
（左辺）と（右辺）が等しくなるためには
$\int_{-\pi}^{\pi}f(x)\cos mxdx=a_m\pi$
$a_m=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos mxdx$

(4.3)←
$f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos nx+ b_n\sin nx)$
の両辺に $\sin mx$ を掛けて $-\pi\underline{\le}x\underline{\le}\pi$ の区間で積分すると
（左辺）= $\int_{-\pi}^{\pi}f(x)\sin mxdx$
（右辺）= $\int_{-\pi}^{\pi}\frac{a_0}{2}\sin mxdx$
$+\sum_{n=1}^{\infty}\{a_n\int_{-\pi}^{\pi}\sin mx\cos nxdx+ b_n\int_{-\pi}^{\pi}\sin mx\sin nxdx\}$
ここで，(1.2)により
$\int_{-\pi}^{\pi}\frac{a_0}{2}\sin mxdx=0$
(3.3)(3.5)により，m≠nのときは消えるから
$\sum_{n=1}^{\infty}b_n\int_{-\pi}^{\pi}\sin mx\sin nxdx=b_m\pi$
(3.1)により
$\sum_{n=1}^{\infty}b_n\int_{-\pi}^{\pi}\sin mx\cos nxdx=0$
以上から，（右辺）= $b_m\pi$
（左辺）と（右辺）が等しくなるためには
$\int_{-\pi}^{\pi}f(x)\sin mxdx=b_m\pi$
$b_m=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin mxdx$

※上記のようにして求めた(4.1)(4.2)(4.3)は
$f(x)=\frac{a_0}{2}+ (a_1\cos x+ b_1\sin x)+(a_2\cos 2x+ b_2\sin 2x)\cdots$
となるために係数が満たすべき必要条件となっています．一定の条件を満たす関数については，このようにして求めた係数により，実際に
$f(x)=\frac{a_0}{2}+ (a_1\cos x+ b_1\sin x)+(a_2\cos 2x+ b_2\sin 2x)\cdots$
が成り立つこと（十分条件も満たされること）は，「ディりクレーの定理」によって示されるが，この教材ではそこまで踏み込まないことにする

３．奇関数・偶関数の積分

後の計算を行うときに，奇関数・偶関数の積分に関する次の性質を使うと，計算の見通しがよく，計算が簡単になります．

L>0とする
$\int_{-L}^{L}$ (奇関数) $dx=0$ …(5.1)
$\int_{-L}^{L}$ (偶関数) $dx=$ $2\int_{0}^{L}$ (偶関数) $dx$ …(5.2)

（5.1の例）
xは奇関数
$\int_{-1}^{1}xdx=\left[\frac{x^2}{2}\right]_{-1}^{1}=0$
sin xは奇関数
$\int_{-\pi}^{\pi}\sin xdx=\left[\frac{\cos x}{n}\right]_{-\pi}^{\pi}=0$
（5.1の図解）

奇関数のグラフは原点対称なので，−L～0までの積分と0～Lまでの積分は符号が逆になり，全部足せば0になる．

（5.1の証明）
$f(x)$ が奇関数であるとき， $f(-x)=-f(x)$ が成り立つ．
そこで

$x=-t$ とおく置換積分を行うと

$x$	$-L\rightarrow 0$
$t$	$L\rightarrow 0$

$f(x)=f(-t)=-f(t)$
$dx=-dt$

$\int_{-L}^0 f(x)dx$
$=\int_{L}^0\{-f(t)\}(-dt)$
$=-\int_{0}^L f(t)dt$
だから
$\int_{-L}^L f(x)dx=\int_{-L}^0 f(x)dx+\int_{0}^L f(x)dx$
$=-\int_{0}^L f(t)dt+\int_{0}^L f(x)dx=0$

（5.2の例）
x²は偶関数
$\int_{-1}^{1}x^2dx=\left[\frac{x^3}{3}\right]_{-1}^{1}=2\times\frac{1}{3}$
cos xは偶関数
$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos xdx=$ $\left[\sin x\right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}$ $=2\times\sin\frac{\pi}{2}=2$
（5.2の図解）

偶関数のグラフはｙ軸対称（左右対称）なので，−L～0までの積分と0～Lまでの積分は同じになり，全体は右半分の２倍になる．
（5.2の証明）
$f(x)$ が偶関数であるとき， $f(-x)=f(x)$ が成り立つ．

そこで

$x=-t$ とおく置換積分を行うと

$x$	$-L\rightarrow 0$
$t$	$L\rightarrow 0$

$f(x)=f(-t)=f(t)$
$dx=-dt$

$\int_{-L}^0 f(x)dx$
$=\int_{L}^0f(t)(-dt)$
$=\int_{0}^L f(t)dt$
だから
$\int_{-L}^L f(x)dx=\int_{-L}^0 f(x)dx+\int_{0}^L f(x)dx$
$=\int_{0}^L f(t)dt+\int_{0}^L f(x)dx=2\int_{0}^L f(x)dx$

４．偶関数と奇関数の組合せ(まとめ)

(奇関数)×(奇関数)=(偶関数)…(6.1)
(奇関数)×(偶関数)=(奇関数)…(6.2)
(偶関数)×(偶関数)=(偶関数)…(6.3)
なお，奇関数を定数倍したものは奇関数，偶関数を定数倍したものは偶関数になる…(6.4)

(奇関数)±(奇関数)=(奇関数)…(6.5)
(奇関数)±(偶関数)→奇関数でも偶関数でもない…(6.6)
(偶関数)±(偶関数)=(偶関数)…(6.7)
なお，0以外の定数項は偶関数…(6.8)

※奇数，偶数の話（奇数×奇数=奇数，奇数×偶数=偶数，偶数×偶数=偶数）と混同しないように！

（6.1の例）
$x\times x^3=x^4$ は偶関数
$x\sin x$ は偶関数
（6.1の証明）
$f_1(x)\hspace{1},\hspace{2}f_2(x)$ を奇関数とすると
$f_1(-x)=-f_1(x)\hspace{1},\hspace{2}f_2(-x)=-f_2(x)$ が成り立つ
このとき，これらの積によって定義される関数 $g(x)=f_1(x)f_2(x)$ について
$g(-x)=f_1(-x)f_2(-x)=\{-f_1(x)\}\{-f_2(x)\}$
$=f_1(x)f_2(x)=g(x)$
が成り立つから， $g(x)$ は偶関数

（6.2の例）
$x\times x^2=x^3$ は奇関数
$x\cos x$ は奇関数
（6.2の証明）
$f_1(x)$ は奇関数， $f_2(x)$ は偶関数とすると
$f_1(-x)=-f_1(x)\hspace{1},\hspace{2}f_2(-x)=f_2(x)$ が成り立つ
このとき，これらの積によって定義される関数 $g(x)=f_1(x)f_2(x)$ について
$g(-x)=f_1(-x)f_2(-x)=\{-f_1(x)\}\{f_2(x)\}$
$=-f_1(x)f_2(x)=-g(x)$
が成り立つから， $g(x)$ は奇関数

（6.3の例）
$x^2\times x^4=x^6$ は偶関数
$x^2\cos x$ は偶関数
（6.3の証明）
$f_1(x)\hspace{1},\hspace{2}f_2(x)$ は偶関数とすると
$f_1(-x)=f_1(x)\hspace{1},\hspace{2}f_2(-x)=f_2(x)$ が成り立つ
このとき，これらの積によって定義される関数 $g(x)=f_1(x)f_2(x)$ について
$g(-x)=f_1(-x)f_2(-x)=f_1(x)f_2(x)=g(x)$
が成り立つから， $g(x)$ は偶関数

（6.4の例）
$3x\hspace{2},\hspace{2}4x$ は奇関数
$3(-x)=-3x\hspace{2},\hspace{3}4(-x)=-4x$
$2\sin x\hspace{2},\hspace{2}3\sin 2x$ は奇関数
$2\sin (-x)=-2\sin x\hspace{2},\hspace{3}3\sin 2(-x)=-3\sin 2x$
（6.4の証明）
$f(x)$ を奇関数とすると $f(-x)=-f(x)$ が成り立つ． $k$ は定数とする．
$g(x)=kf(x)$ とおくと
$g(-x)=kf(-x)=-kf(x)=-g(x)$ となるから， $g(x)$ は奇関数

$f(x)$ を偶関数とすると $f(-x)=f(x)$ が成り立つ． $k$ は定数とする．
$g(x)=kf(x)$ とおくと
$g(-x)=kf(-x)=kf(x)=g(x)$ となるから， $g(x)$ は偶関数

（6.5の例）
$2\sin x+ 3\sin 2x$ は奇関数
$\sin 3x-5\sin 4x$ は奇関数
（6.5の証明）
$f_1(x)\hspace{1},\hspace{2}f_2(x)$ を奇関数とすると $f_1(-x)=-f_1(x)\hspace{1},\hspace{2}f_2(-x)=-f_2(x)$ が成り立つ．
$g(x)=f_1(x)+ f_2(x)$ とおくと
$g(-x)=f_1(-x)+ f_2(-x)$
$=-f_1(x)-f_2(x)=-g(x)$
となるから， $g(x)$ は奇関数 $f_1(x)-f_2(x)$ についても同様に示される

（6.6の例）
$f(x)=x+ x^2$ は奇関数でも偶関数でもない

$f(-x)=(-x)+ (-x)^2=-x+ x^2$ が，つねに $f(x)=x+ x^2$ または $-f(x)=-x- x^2$ に等しい訳ではない

$f(x)=\sin x+\cos x$ は奇関数でも偶関数でもない

$f(-x)=\sin(-x)+\cos(-x)=-\sin x+\cos x$ が，つねに $f(x)=\sin x+\cos x$ または $-f(x)=-\sin x-\cos x$ に等しい訳ではない

（6.7の例）
$2\cos x+ 3\cos 2x$ は偶関数
$\cos x-3\cos 2x$ は偶関数
（6.7の証明）
$f_1(x)\hspace{1},\hspace{2}f_2(x)$ を偶関数とすると $f_1(-x)=f_1(x)\hspace{1},\hspace{2}f_2(-x)=f_2(x)$ が成り立つ．
$g(x)=f_1(x)+ f_2(x)$ とおくと
$g(-x)=f_1(-x)+ f_2(-x)$
$=f_1(x)+ f_2(x)=g(x)$
となるから， $g(x)$ は偶関数 $f_1(x)-f_2(x)$ についても同様に示される

（6.8の例）
$f(x)=3$ は偶関数
$f(x)=-2$ は偶関数
（6.8の証明）
$f(x)=k\hspace{5}(k\ne 0)$ とすると， $f(-x)=k=f(x)$ が成り立つから $f(x)=k\hspace{5}(k\ne 0)$ は偶関数

５． $f(x)=x$ とおくと

(4.1)→
$a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}xdx=\left[\frac{x^2}{2}\right]_{-\pi}^{\pi}=0$
(4.2)→
$a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}x\cos nxdx$

$x=f(x)\hspace{2},\hspace{2}\cos nx=g\apos(x)$ とおいて部分積分を行う

$x=f(x)$	$1=f\apos(x)$
$\cos nx=g\apos(x)$	$\frac{\sin nx}{n}=g(x)$

$a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)g\apos(x)dx$
$=\frac{1}{\pi}\{\left[f(x)g(x)\right]_{-\pi}^{\pi}-\int_{-\pi}^{\pi}f\apos(x)g(x)dx\}$
$=\frac{1}{\pi}\{\left[x\frac{\sin nx}{n}\right]_{-\pi}^{\pi}-\int_{-\pi}^{\pi}\frac{\sin nx}{n}dx\}$
$=\frac{1}{\pi}\{0+\left[\frac{\cos nx}{n^2}\right]_{-\pi}^{\pi}\}$

$\cos\theta$ は偶関数
$\cos (-nx)=\cos nx$

$=\frac{1}{\pi}\{\frac{\cos n\pi-\cos(-n\pi)}{n^2}\}$
$=\frac{1}{\pi}\{\frac{\cos n\pi-\cos n\pi}{n^2}\}=0$
$b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nxdx$ …(5.3)
(4.3)→
$b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}x\sin nxdx$

$x=f(x)\hspace{2},\hspace{2}\sin nx=g\apos(x)$ とおいて部分積分を行う

$x=f(x)$	$1=f\apos(x)$
$\sin nx=g\apos(x)$	$-\frac{\cos nx}{n}=g(x)$

$b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)g\apos(x)dx$
$=\frac{1}{\pi}\{\left[f(x)g(x)\right]_{-\pi}^{\pi}-\int_{-\pi}^{\pi}f\apos(x)g(x)dx\}$
$=\frac{1}{\pi}\{\left[-x\frac{\cos nx}{n}\right]_{-\pi}^{\pi}+\int_{-\pi}^{\pi}\frac{\cos nx}{n}dx\}$
$=\frac{1}{\pi}\{\frac{-\pi\cos n\pi-\pi\cos(-n\pi)}{n}+\left[\frac{\sin nx}{n\2}\right]_{-\pi}^{\pi}\}$
$=\frac{1}{\pi}\{\frac{-\pi\cos n\pi-\pi\cos n\pi}{n}+ 0\}$
$=-2\frac{\cos n\pi}{n}$
これらを使うと
$x=-2\sum_{n=1}^{\infty}\frac{\cos n\pi}{n}\sin nx$ →[1]
と書けることになる．

　このフーリエ級数展開が，元の関数 y=x をどのぐらい再現しているかを調べるために，−3.1415≦x≦3.1415まで0.1刻みに点を取り，n=1～100までのフーリエ多項式でグラフをExcelで作成し，近似式を表示すると，次のようになる．

　太い方の青で示した曲線がフーリエ多項式
$x=-2\sum_{n=1}^{100}\frac{\cos n\pi}{n}\sin nx$
に対応し，黒で示した細い方の直線が近似直線．
　これによれば，y=1.0026xと近似されるのだから，ほぼy=1xが再現できていると考えられる．

この結果において， $x=\frac{\pi}{2}$ の場合を考えると

$\sin nx$ があるから，x=0ちしてしまうと右辺が全部消えてしまい何も残らないので，比較的簡単に計算できる数字として $x=\frac{\pi}{2}$ を選んだ．

$\frac{\pi}{2}=-2\{\frac{\cos \pi}{1}\sin\frac{\pi}{2}+\frac{\cos 2\pi}{2}\sin\pi$
$+\frac{\cos 3\pi}{3}\sin\frac{3\pi}{2}+\frac{\cos 4\pi}{4}\sin 2\pi\cdots\}$
$\frac{\pi}{2}=-2\{-1+ 0+\frac{1}{3}+ 0-\frac{1}{5}+\frac{1}{7}+\cdots\}$
ゆえに
$1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots=\frac{\pi}{4}$ →②

※(6.5)～(6.8)を用いると，上記の答案は格段に短縮できる．
すなわち，求める関数 $x$ は奇関数であるから，偶関数の係数 $a_0,\hspace{2}a_n$ はすべて0でなければならない．したがって， $b_n$ の計算だけを行えばよいことが分かる．

６． $f(x)=|x|$ とおくと

求める関数 $|x|$ は偶関数であるから， $b_n$ はすべて0でなければならない．また，偶関数であるから
$\int_{-\pi}^{\pi}f(x)dx=2\int_0^{\pi}f(x)dx$
を利用できる．
(4.1)→
$a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}|x|dx=\frac{2}{\pi}\int_{0}^{\pi}xdx=\frac{2}{\pi}\left[\frac{x^2}{2}\right]_0^{\pi}$
$=\frac{2}{\pi}\cdot\frac{\pi^2}{2}=\pi$
(4.2)→
$a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}|x|\cos nxdx$
被積分関数は偶関数だから，右半分の２倍で計算できる
$=\frac{2}{\pi}\int_{0}^{\pi}x\cos nxdx$

$x=f(x)\hspace{2},\hspace{2}\cos nx=g\apos(x)$ とおいて部分積分を行う

$x=f(x)$	$1=f\apos(x)$
$\cos nx=g\apos(x)$	$\frac{\sin nx}{n}=g(x)$

$=\frac{2}{\pi}\{\left[x\frac{\sin nx}{n}\right]_0^{\pi}-\int_0^{\pi}\frac{\sin nx}{n}dx\}$
$=\frac{2}{\pi}\{0+\left[\frac{\cos nx}{n^2}\right]_0^{\pi}\}$
$=\frac{2}{\pi}\cdot\frac{\cos n\pi-1}{n^2}$
結局， $|x|$ のフーリエ級数展開は，次の式になる．
$|x|=\frac{\pi}{2}+\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{\cos n\pi-1}{n^2}\cos nx$ →[2]

　このフーリエ級数展開が，元の関数 y=|x| をどのぐらい再現しているかを調べるために，−3.1415≦x≦3.1415まで0.1刻みに点を取り，n=1～100までのフーリエ多項式でグラフをExcelで作成すると，次のようになる．

　これによれば，ほぼy=|x|が再現できていると考えられる．

この式において，x=0とおくと，次の和が得られる．
$0=\frac{\pi}{2}+\frac{2}{\pi}\{\frac{-2}{1^2}+\frac{0}{2^2}+\frac{-2}{3^2}+\frac{0}{4^2}+\frac{-2}{5^2}+\cdots\}$
$-\frac{\pi}{2}=\frac{-4}{\pi}\{\frac{1}{1^2}+\frac{1}{3^2}+\frac{1}{5^2}+\cdots\}$
$\frac{1}{1^2}+\frac{1}{3^2}+\frac{1}{5^2}+\cdots=\frac{\pi^2}{8}$ →⑤

７． $f(x)=x^2$ とおくと

求める関数 $x^2$ は偶関数であるから， $b_n$ はすべて0でなければならない．また，偶関数であるから
$\int_{-\pi}^{\pi}f(x)dx=2\int_0^{\pi}f(x)dx$
を利用できる．
(4.1)→
$a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}x^2dx=\frac{2}{\pi}\int_{0}^{\pi}x^2dx=\frac{2}{\pi}\left[\frac{x^3}{3}\right]_0^{\pi}$
$=\frac{2}{\pi}\cdot\frac{\pi^3}{3}=\frac{2}{3}\pi^2$
(4.2)→
$a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}x^2\cos nxdx$
被積分関数は偶関数だから，右半分の２倍で計算できる
$=\frac{2}{\pi}\int_{0}^{\pi}x^2\cos nxdx$

$x^2=f(x)\hspace{2},\hspace{2}\cos nx=g\apos(x)$ とおいて部分積分を行う

$x^2=f(x)$	$2x=f\apos(x)$
$\cos nx=g\apos(x)$	$\frac{\sin nx}{n}=g(x)$

$=\frac{2}{\pi}\{\left[x^2\frac{\sin nx}{n}\right]_0^{\pi}-\int_0^{\pi}2x\frac{\sin nx}{n}dx\}$
$=\frac{2}{\pi}\{0-\frac{2}{n}\int_0^{\pi}x\sin nxdx\}$

$x=p(x)\hspace{2},\hspace{2}\sin nx=q\apos(x)$ とおいて部分積分を行う

$x=p(x)$	$1=p\apos(x)$
$\sin nx=q\apos(x)$	$\frac{-\cos nx}{n}=q(x)$

$=-\frac{4}{n\pi}\{\left[-x\frac{\cos nx}{n}\right]_0^{\pi}+\int_0^{\pi}\frac{\cos nx}{n}dx\}$
$=-\frac{4}{n\pi}\{-\pi\frac{\cos n\pi}{n}-0+\left[\frac{\sin nx}{n^2}\right]_0^{\pi}\}$
$=\frac{4\cos n\pi}{n^2}$
結局， $x^2$ のフーリエ級数展開は，次の式になる．
$x^2=\frac{\pi^2}{3}+ 4\sum_{n=1}^{\infty}\frac{\cos n\pi}{n^2}\cos nx$ →[4]

　このフーリエ級数展開が，元の関数 y=x² をどのぐらい再現しているかを調べるために，−3.1415≦x≦3.1415まで0.1刻みに点を取り，n=1～100までのフーリエ多項式でグラフをExcelで作成し，近似式を表示すると，次のようになる．

　太い方の青で示した曲線がフーリエ多項式
$x^2=\frac{\pi^2}{3}+ 4\sum_{n=1}^{\infty}\frac{\cos n\pi}{n^2}\cos nx$
に対応し，黒で示した細い方の直線が近似直線．
　これによれば，ほぼy=x²が再現できていると考えられる．

この式において，x=0とおくと，次の和が得られる．
$0=\frac{\pi^2}{3}+ 4\{\frac{-1}{1^2}+\frac{1}{2^2}+\frac{-1}{3^2}+\frac{1}{4^2}+\cdots\}$
$-\frac{\pi^2}{3}=4\{-\frac{1}{1^2}+\frac{1}{2^2}-\frac{1}{3^2}+\frac{1}{4^2}+\cdots\}$
$\frac{1}{1^2}-\frac{1}{2^2}+\frac{1}{3^2}-\frac{1}{4^2}+\cdots=\frac{\pi^2}{12}$ →④

6.の結果から
$S=\frac{1}{1^2}+\frac{1}{3^2}+\frac{1}{5^2}+\cdots=\frac{\pi^2}{8}$
$T=\frac{1}{2^2}+\frac{1}{4^2}+\frac{1}{6^2}+\cdots$
とおくと，7.の結果から
$S-T=\frac{1}{1^2}-\frac{1}{2^2}+\frac{1}{3^2}-\frac{1}{4^2}+\cdots=\frac{\pi^2}{12}$
したがって
$T=\frac{1}{2^2}+\frac{1}{4^2}+\frac{1}{6^2}+\cdots=\frac{\pi^2}{8}-\frac{\pi^2}{12}=\frac{\pi^2}{24}$ →⑥
$S+ T=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots=\frac{\pi^2}{6}$ →③

８．方形波（矩形波）のフーリエ級数展開

　右図のような
$f(x)=\{\begin{matrix}-1\hspace{5}(x\lt 0)\\ 0\hspace{5}(x=0)\\ 1\hspace{5}(x\gt 0)\end{matrix}$
で定義される関数は方形波（矩形波）と呼ばれる．この方形波（矩形波）のフーリエ級数展開を考えてみる．
　この関数は，奇関数だから， $a_0,\hspace{2}a_n$ はすべて0になる．
(4.3)→
$b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nxdx$
$=\frac{1}{\pi}\int_{-\pi}^{0}(-\sin nx)dx+\frac{1}{\pi}\int_{0}^{\pi}\sin nxdx$

$x=-t$ とおいて第１項を置換積分で変形する

$x$	$-\pi\rightarrow 0$
$t$	$\pi\rightarrow 0$

$dx=-dt$
$\int_{-\pi}^{0}(-\sin nx)dx=\int_{\pi}^0\{-\sin(-nt)(-dt)\}$
$=\int_{\pi}^0(-\sin ntdt)=\int_0^{\pi}\sin ntdt$

これにより，第１項と第２項は等しいことが分かるから
$b_n=\frac{2}{\pi}\int_{0}^{\pi}\sin nxdx=\frac{2}{\pi}\left[\frac{-\cos n\pi}{n}\right]_0^{\pi}=\frac{2}{\pi}\cdot\frac{-\cos nx+ 1}{n}$
結局，方形波のフーリエ級数展開は，次の式になる．
$f(x)=\frac{2}{\pi}\sum_{n=1}^{\infty}\frac{1-\cos n\pi}{n}\sin nx$ →[3]

　このフーリエ級数展開が，元の方形波（矩形波）をどのぐらい再現しているかを調べるために，−3.1415≦x≦3.1415まで0.1刻みに点を取り，n=1～100までのフーリエ多項式でグラフをExcelで作成すると，次のようになる．

　これによれば，階段の角の所にギップス現象と呼ばれる「ツノ」ができるのが特徴であるが，全体的にはよく再現できていると考えられる．

この式において， $x=\frac{\pi}{2}$ とおくと，左辺は定義により1となるから
$1=\frac{2}{\pi}\{\frac{2}{1}\times 1+ 0+\frac{2}{3}\times(-1)+ 0+\frac{2}{5}\times 1+ 0+\cdots\}$
$=\frac{4}{\pi}\{\frac{1}{1}-\frac{1}{3}+\frac{1}{5}+\cdots\}$
したがって
$\frac{1}{1}-\frac{1}{3}+\frac{1}{5}+\cdots=\frac{\pi}{4}$
となって，５．の結果と一致する

９． $f(x)=x^3$ とおくと

求める関数 $x^3$ は奇関数であるから， $a_0,\hspace{3}a_n$ はすべて0でなければならない．
(4.3)→
$b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}x^3\sin nxdx$

ここで
$\frac{1}{\pi}\int_{\pi}^{0}x^3\sin nxdx$
は置換積分により，右半分と等しいことが示せる．
　すなわち， $x=-t$ とおいて第１項を置換積分で変形すると

$x$	$-\pi\rightarrow 0$
$t$	$\pi\rightarrow 0$

$dx=-dt$
$\int_{-\pi}^{0}x^3\sin nxdx=\int_{\pi}^0(-t)^3\sin (-nt)(-dt)\}$
$=\int_{\pi}^0(-t^3\sin ntdt)=\int_0^{\pi}t^3\sin ntdt$

したがって，次の形に書ける．
$b_n=\frac{2}{\pi}\int_{0}^{\pi}x^3\sin nxdx$
部分積分を３回繰り返して， $x^3$ の次数を下げる．

$x^3=f(x)\hspace{2},\hspace{2}\sin nx=g\apos(x)$ とおいて部分積分を行う

$x^3=f(x)$	$3x^2=f\apos(x)$
$\sin nx=g\apos(x)$	$\frac{-\cos nx}{n}=g(x)$

$b_n=\frac{2}{\pi}\{\left[\frac{-x^3\cos nx}{n}\right]_0^{\pi}+\frac{3}{n}\int_0^{\pi}x^2\cos nx\}$
$=\frac{2}{\pi}\{\frac{-\pi^3\cos n\pi}{n}+\frac{3}{n}\int_0^{\pi}x^2\cos nx\}$

$x^2=p(x)\hspace{2},\hspace{2}\cos nx=q\apos(x)$ とおいて部分積分を行う

$x^2=p(x)$	$2x=p\apos(x)$
$\cos nx=q\apos(x)$	$\frac{\sin nx}{n}=q(x)$

$=\frac{2}{\pi}\{\frac{-\pi^3\cos n\pi}{n}+\frac{3}{n}\left(\left[\frac{x^2\sin nx}{n}\right]_0^{\pi}-\frac{2}{n}\int_0^{\pi}x\sin nxdx\right)\}$
$=\frac{2}{\pi}\{\frac{-\pi^3\cos n\pi}{n}+\frac{3}{n}\left(0-\frac{2}{n}\int_0^{\pi}x\sin nxdx\right)\}$
$=\frac{2}{\pi}\{\frac{-\pi^3\cos n\pi}{n}-\frac{6}{n^2}\int_0^{\pi}x\sin nxdx\}$

$x=u(x)\hspace{2},\hspace{2}\sin nx=v\apos(x)$ とおいて部分積分を行う

$x=u(x)$	$1=u\apos(x)$
$\sin nx=v\apos(x)$	$\frac{-\cos nx}{n}=v(x)$

$=\frac{2}{\pi}\{\frac{-\pi^3\cos n\pi}{n}-\frac{6}{n^2}\left(\left[\frac{-x\cos nx}{n}\right]_0^{\pi}+\int_0^{\pi}\frac{\cos nx}{n}dx\right)\}$
$=\frac{2}{\pi}\{\frac{-\pi^3\cos n\pi}{n}-\frac{6}{n^2}\left(\frac{-\pi\cos n\pi}{n}+\left[\frac{\sin nx}{n^2}\right]_0^{\pi}\right)\}$
$=\frac{2}{\pi}\{\frac{-\pi^3\cos n\pi}{n}-\frac{6}{n^2}\left(\frac{-\pi\cos n\pi}{n}+ 0\right)\}$
$=-\frac{2\pi^2\cos n\pi}{n}+\frac{12\cos n\pi}{n^3}$
したがって， $x^3\hspace{5}(-\pi\underline{\le}x\underline{\le}\pi)$ のフーリエ級数展開は次の式になる．
$x^3=\sum_{n=1}^{\infty}\left(-\frac{2\pi^2\cos n\pi}{n}+\frac{12\cos n\pi}{n^3}\right)\sin nx$ →[5]

　このフーリエ級数展開が，元の関数 y=x³ をどのぐらい再現しているかを調べるために，−3.1415≦x≦3.1415まで0.1刻みに点を取り，n=1～100までのフーリエ多項式でグラフをExcelで作成し，近似式を表示すると，次のようになる．

　太い方の青で示した曲線がフーリエ多項式
$x^3=\sum_{n=1}^{100}\left(-\frac{2\pi^2\cos n\pi}{n}+\frac{12\cos n\pi}{n^3}\right)\sin nx$
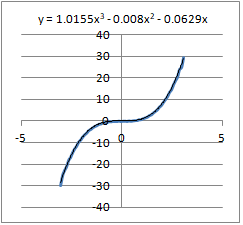に対応し，黒で示した細い方の直線が近似直線．
　これを見ると， $y=1x^3-0x^2-0x$ がほぼ再現されていると考えられる．

$x=\frac{\pi}{2}$ のときの式の値を求めると
$\frac{\pi^3}{8}=(2\pi^2-12)-(\frac{2\pi^2}{3}-\frac{12}{3^3})+(\frac{2\pi^2}{5}-\frac{12}{5^3})-\cdots$
$=2\pi^2(1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots)-12(1-\frac{1}{3^3}+\frac{1}{5^3}-\cdots)$
5.の結果から
$1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots=\frac{\pi}{4}$
だから
$\frac{\pi^3}{8}=2\pi^2\cdot\frac{\pi}{4}-12(1-\frac{1}{3^3}+\frac{1}{5^3}-\cdots)$
$-\frac{3}{8}\pi^3=-12(1-\frac{1}{3^3}+\frac{1}{5^3}-\cdots)$
$1-\frac{1}{3^3}+\frac{1}{5^3}-\cdots=\frac{\pi^3}{32}$ →⑧
一般に，sが正の奇数のとき
$1+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\cdots$
は簡単な分数では書けない．

10． $f(x)=x^4$ とおくと

求める関数 $x^4$ は偶関数であるから， $b_n$ はすべて0でなければならない．
(4.1)→
$a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}x^4 dx=\frac{2}{\pi}\int_{0}^{\pi}x^4 dx=\frac{2}{\pi}\left[\frac{x^5}{5}\right]_0^{\pi}=\frac{2}{5}\pi^4$
(4.2)→
$a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}x^4\cos nx dx=\frac{2}{\pi}\int_{0}^{\pi}x^4\cos nx dx$
部分積分を４回繰り返して， $x^4$ の次数を下げる．

$x^4=f(x)\hspace{2},\hspace{2}\cos nx=g\apos(x)$ とおいて部分積分を行う

$x^4=f(x)$	$4x^3=f\apos(x)$
$\cos nx=g\apos(x)$	$\frac{\sin nx}{n}=g(x)$

$a_n=\frac{2}{\pi}\{\left[x^4\cdot\frac{\sin nx}{n}\right]_0^{\pi}-\frac{4}{n}\int_0^{\pi}x^3\sin nxdx\}$
$=\frac{2}{\pi}\{0-\frac{4}{n}\int_0^{\pi}x^3\sin nxdx\}$
$=-\frac{8}{n\pi}\int_0^{\pi}x^3\sin nxdx$

$x^3=p(x)\hspace{2},\hspace{2}\sin nx=q\apos(x)$ とおいて部分積分を行う

$x^3=p(x)$	$3x^2=p\apos(x)$
$\sin nx=q\apos(x)$	$\frac{-\cos nx}{n}=q(x)$

$=-\frac{8}{n\pi}\{\left[-\frac{x^3\cos nx}{n}\right]_0^{\pi}+\frac{3}{n}\int_0^{\pi}x^2\cos nxdx\}$
$=-\frac{8}{n\pi}\{-\frac{\pi^3\cos n\pi}{n}+\frac{3}{n}\int_0^{\pi}x^2\cos nxdx\}$

$x^2=u(x)\hspace{2},\hspace{2}\cos nx=v\apos(x)$ とおいて部分積分を行う

$x^2=u(x)$	$2x=u\apos(x)$
$\cos nx=v\apos(x)$	$\frac{\sin nx}{n}=v(x)$

$=-\frac{8}{n\pi}\{-\frac{\pi^3\cos n\pi}{n}+\frac{3}{n}\left(\left[x^2\cdot\frac{sin nx}{n}\right]_0^{\pi}-\frac{2}{n}\int_0^{\pi}x\sin nxdx\right)\}$
$=-\frac{8}{n\pi}\{-\frac{\pi^3\cos n\pi}{n}+\frac{3}{n}\left(0-\frac{2}{n}\int_0^{\pi}x\sin nxdx\right)\}$
$=-\frac{8}{n\pi}\{-\frac{\pi^3\cos n\pi}{n}-\frac{6}{n^2}\int_0^{\pi}x\sin nxdx\}$

$x=w(x)\hspace{2},\hspace{2}\sin nx=z\apos(x)$ とおいて部分積分を行う

$x=w(x)$	$1=w\apos(x)$
$\sin nx=z\apos(x)$	$\frac{-\cos nx}{n}=z(x)$

$=-\frac{8}{n\pi}\{-\frac{\pi^3\cos n\pi}{n}-\frac{6}{n^2}\left(\left[\frac{-x\cos nx}{n}\right]_0^{\pi}-\int_0^{\pi}\frac{-\cos nx}{n}dx\right)\}$
$=-\frac{8}{n\pi}\{-\frac{\pi^3\cos n\pi}{n}-\frac{6}{n^2}\left(\frac{-\pi\cos n\pi}{n}-\int_0^{\pi}\frac{-\cos nx}{n}dx\right)\}$
$=-\frac{8}{n\pi}\{-\frac{\pi^3\cos n\pi}{n}+\frac{6\pi\cos n\pi}{n^3}-\frac{6}{n^3}\int_0^{\pi}\cos nxdx\}$
$=-\frac{8}{n\pi}\{-\frac{\pi^3\cos n\pi}{n}+\frac{6\pi\cos n\pi}{n^3}-\frac{6}{n^3}\left[\frac{\sin nx}{n}\right]_0^{\pi}\}$
$=-\frac{8}{n\pi}\{-\frac{\pi^3\cos n\pi}{n}+\frac{6\pi\cos n\pi}{n^3}-0\}$
$=\frac{8}{n^2}\left(\frac{\pi^2\cos n\pi}{n}-\frac{6\cos n\pi}{n^2}\right)$
$=\frac{8}{n^2}\left(\pi^2-\frac{6}{n^2}\right)\cos n\pi$
したがって， $x^4\hspace{5}(-\pi\underline{\le}x\underline{\le}\pi)$ のフーリエ級数展開は次の式になる．
$x^4=\frac{\pi^4}{5}+\sum_{n=1}^{\infty}\frac{8}{n^2}\left(\pi^2-\frac{6}{n^2}\right)\cos n\pi\cos nx$ →[6]

　このフーリエ級数展開が，元の関数 y=x⁴ をどのぐらい再現しているかを調べるために，−3.1415≦x≦3.1415まで0.1刻みに点を取り，n=1～100までのフーリエ多項式でグラフをExcelで作成し，近似式を表示すると，次のようになる．

　太い方の青で示した曲線がフーリエ多項式
$x^4=\frac{\pi^4}{5}+\sum_{n=1}^{100}\frac{8\pi}{n^2}\left(\pi^2-\frac{6}{n^2}\right)\cos n\pi\cos nx$
に対応し，黒で示した細い方の直線が近似直線．
　これを見ると， $y=1x^4+ 0x^3+ 0x^2-0x-0$ がほぼ再現されていると考えられる．

$x=0$ のとき
$0=\frac{\pi^4}{5}+ 8(\pi^2-6)\cdot(-1)+ \frac{8}{2^2}(\pi^2-\frac{6}{2^2})\cdot 1+\frac{8}{3^2}(\pi^2-\frac{6}{3^2})\cdot(-1)$
$+\frac{8}{4^2}(\pi^2-\frac{6}{4^2})\cdot 1+\frac{8}{5^2}(\pi^2-\frac{6}{5^2})\cdot(-1)+\cdots$
$-\frac{\pi^4}{5}=8\{(\pi^2-6)\cdot(-1)+ \frac{1}{2^2}(\pi^2-\frac{6}{2^2})\cdot 1$ $+\frac{1}{3^2}(\pi^2-\frac{6}{3^2})\cdot(-1)+\frac{1}{4^2}(\pi^2-\frac{6}{4^2})\cdot 1+\frac{1}{5^2}(\pi^2-\frac{6}{5^2})\cdot(-1)+\cdots\}$
$-\frac{\pi^4}{40}=\pi^2(-\frac{1}{1^2}+\frac{1}{2^2}-\frac{1}{3^2}+\cdots)+ 6(\frac{1}{1^4}-\frac{1}{2^4}+\frac{1}{3^4}-\cdots)$
ここで７．の結果から
$\frac{1}{1^2}-\frac{1}{2^2}+\frac{1}{3^2}-\cdots=\frac{\pi^2}{12}$ だから，
$-\frac{\pi^4}{40}=\pi^2(-\frac{\pi^2}{12})+ 6(\frac{1}{1^4}-\frac{1}{2^4}+\frac{1}{3^4}-\cdots)$
$6(\frac{1}{1^4}-\frac{1}{2^4}+\frac{1}{3^4}-\cdots)=\frac{7}{120}\pi^4$
$\frac{1}{1^4}-\frac{1}{2^4}+\frac{1}{3^4}-\frac{1}{4^4}\cdots=\frac{7}{720}\pi^4$ →⑩
ここで，
$S=\frac{1}{1^4}+\frac{1}{2^4}+\frac{1}{3^4}+\frac{1}{4^4}+\cdots$ とおくと
$\frac{1}{2^4}+\frac{1}{4^4}+\frac{1}{6^4}+\frac{1}{8^4}+\cdots=\frac{S}{16}$ だから
$S-2\times\frac{S}{16}=\frac{1}{1^4}-\frac{1}{2^4}+\frac{1}{3^4}-\frac{1}{4^4}+\cdots=\frac{7}{720}\pi^4$
$\frac{7}{8}S=\frac{7}{720}\pi^4$
$S=\frac{1}{1^4}+\frac{1}{2^4}+\frac{1}{3^4}+\frac{1}{4^4}+\cdots=\frac{\pi^4}{90}$ →⑨

$\frac{1}{1}-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots=\log 2$ →(*1)
この級数の和は，テイラー級数（マクローリン級数）で考える方が簡単になる．すなわち，
$\log(1+ x)=\frac{x}{1}-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\cdots\hspace{5}(-1\lt x\underline{\le}1)$
においてx=1を代入すると
$\frac{1}{1}-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots=\log 2$
が得られる．

11．パーセバルの等式

$f(x)=x^n$ の $n$ が大きな整数になると，次の(4.2)(4.3)によってフーリエ係数を求めようとすると，部分積分をn回繰り返さなければならず，計算が大変になる．
$a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nxdx$ …(4.2)
$b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nxdx$ …(4.3)
　このとき，フーリエ級数に関するパーセバルの等式を利用すると $f(x)=x^n$ のフーリエ係数をもっと楽に計算できる．

　まず，［無限次元空間におけるベクトル］について成り立つ関係を思い出すと
$\vec{e_m},\hspace{5}\vec{e_n}$ を互いに垂直で大きさ1の基本ベクトルとするとき
$\vec{e_m}\cdot\vec{e_n}=\{\begin{matrix}0\hspace{5}(m\ne n)\\ 1\hspace{5}(m=n)\end{matrix}$
だから
$\vec{v}=a_1\vec{e_1}+ a_2\vec{e_2}+ a_3\vec{e_3}+\cdots$
となるベクトルについて
$|\vec{v}|^2=\vec{v}\cdot\vec{v}$
$=(a_1\vec{e_1}+ a_2\vec{e_2}+ a_3\vec{e_3}+\cdots)\cdot(a_1\vec{e_1}+ a_2\vec{e_2}+ a_3\vec{e_3}+\cdots)$

$=\sum_{n=1}^{\infty}a_n^2$ …(11.1)

が成り立つ．（ピタゴラスの定理，パーセバルの等式と呼ばれる）
　また，ベクトルの内積から，
$\vec{v}=a_1\vec{e_1}+ a_2\vec{e_2}+ a_3\vec{e_3}+\cdots$
$\vec{w}=b_1\vec{e_1}+ b_2\vec{e_2}+ b_3\vec{e_3}+\cdots$
のとき

$\vec{v}\cdot\vec{w}=a_1b_1+ a_2b_2+ a_3b_3+\cdots$ …(11.2)

が成り立つ．

　フーリエ級数
$f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos nx+ b_n\sin nx)$
については，同一物との積の積分が１，異なる物との積の積分が0ということから，上と類似の次の関係が成り立つ．

$\frac{1}{\pi}\int_{-\pi}^{\pi}f^2(x)dx=\frac{a_0^2}{2}+\sum_{n=1}^{\infty}(a_n^2+ b_n^2)$ …(11.3)

(11.3)はフーリエ係数に関するパーセバルの等式と呼ばれる．

（証明）
$\frac{1}{\pi}\int_{-\pi}^{\pi}f^2(x)dx$
$=\frac{1}{\pi}\int_{-\pi}^{\pi}\{\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos nx+ b_n\sin nx)\}^2dx$
まず
$\frac{1}{\pi}\int_{-\pi}^{\pi}\frac{a_0}{2}\{\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos nx+ b_n\sin nx)\}dx$
のうちで，初めの項は
$\frac{1}{\pi}\int_{-\pi}^{\pi}\{\frac{a_0}{2}\}^2dx=\frac{2}{\pi}\int_{0}^{\pi}\{\frac{a_0}{2}\}^2dx$
$=\frac{2}{\pi}\left[\frac{a_0^2}{4}x\right]_0^{\pi}=\frac{2}{\pi}\cdot\frac{a_0^2}{4}\pi=\frac{a_0^2}{2}$
次に
$\int_{-\pi}^{\pi}\sin nxdx=0$ …(1.2)
$\int_{-\pi}^{\pi}\cos nxdx=0$ …(1.3)
だから，他の項は０になって消える．

$\frac{1}{\pi}\int_{-\pi}^{\pi}a_n\cos nx\{\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos nx+ b_n\sin nx)\}dx$
次の関係が成り立つから， $\cos nx\cos nx$ の項だけ残り，他は０になって消える．
$\int_{-\pi}^{\pi}\cos mx\sin nxdx=0$ …(3.1)
m≠nのとき
$\int_{-\pi}^{\pi}\cos mx\cos nxdx=0$ …(3.2)
$\int_{-\pi}^{\pi}\sin mx\sin nxdx=0$ …(3.3)
m=nのとき
$\int_{-\pi}^{\pi}\cos mx\cos nxdx=\pi$ …(3.4)
$\int_{-\pi}^{\pi}\sin mx\sin nxdx=\pi$ …(3.5)
$\frac{1}{\pi}\int_{-\pi}^{\pi}a_n\cos nx\cdot a_n\cos nxdx=\frac{2}{\pi}\int_{0}^{\pi}a_n^2\cos^2 nxdx$
$=\frac{2a_n^2}{\pi}\int_{0}^{\pi}\frac{\cos 2nx+ 1}{2}dx=\frac{2a_n^2}{\pi}\left[\frac{\sin 2nx}{2n}+\frac{x}{2}\right]_0^{\pi}$
$=a_n^2$

$\frac{1}{\pi}\int_{-\pi}^{\pi}b_n\sin nx\{\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos nx+ b_n\sin nx)\}dx$
も同様にして， $\sin nx\sin nx$ の項だけ残り，他は０になって消える．
$\frac{1}{\pi}\int_{-\pi}^{\pi}b_n\sin nx\{\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos nx+ b_n\sin nx)\}dx$
$=b_n^2$
以上の項を加えると
$\frac{1}{\pi}\int_{-\pi}^{\pi}f^2(x)dx=\frac{a_0^2}{2}+\sum_{n=1}^{\infty}(a_n^2+ b_n^2)$

　2つのベクトルの内積の関係に対応して
$f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n\cos nx+ b_n\sin nx)$
$g(x)=\frac{c_0}{2}+\sum_{n=1}^{\infty}(c_n\cos nx+ d_n\sin nx)$
のとき

$\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)g(x)dx=\frac{a_0c_0}{2}+\sum_{n=1}^{\infty}(a_nc_n+ b_nd_n)$ …(11.4)

も成り立つはずであるが，教科書に書かれていないのは，使える場面が少ないせいかもしれない．

【パーセバルの等式を利用した計算】
$x=-2\sum_{n=1}^{\infty}\frac{\cos n\pi}{n}\sin nx$ →[1]
に対してパーセバルの等式を適用すると
$\frac{1}{\pi}\int_{-\pi}^{\pi}x^2dx=0+ 4\sum_{n=1}^{\infty}\frac{\cos^2 n\pi}{n^2}$
$\frac{2}{\pi}\left[\frac{x^3}{3}\right]_0^{\pi}=4\{\frac{1}{1^2}+ \frac{1}{2^2}+ \frac{1}{3^2}+\cdots$
$\frac{2\pi^2}{3}=4\{\frac{1}{1^2}+ \frac{1}{2^2}+ \frac{1}{3^2}+\cdots$
$\frac{1}{1^2}+ \frac{1}{2^2}+ \frac{1}{3^2}+\cdots=\frac{\pi^2}{6}$
この結果は③と一致する．

$x^2=\frac{\pi^2}{3}+ 4\sum_{n=1}^{\infty}\frac{\cos n\pi}{n^2}$ →[4]
に対してパーセバルの等式を適用すると
$\frac{1}{\pi}\int_{-\pi}^{\pi}x^4dx=\frac{4\pi^4}{9}\cdot\frac{1}{2}+ 16\sum_{n=1}^{\infty}\frac{\cos^2 n\pi}{n^4}$
$\frac{2\pi^4}{5}=\frac{2\pi^4}{9}+ 16\{\frac{1}{1^4}+ \frac{1}{2^4}+ \frac{1}{3^4}+ \cdots\}$
$\frac{2\pi^4}{5}-\frac{2\pi^4}{9}=16\{\frac{1}{1^4}+ \frac{1}{2^4}+ \frac{1}{3^4}+ \cdots\}$
$\frac{1}{1^4}+ \frac{1}{2^4}+ \frac{1}{3^4}+ \cdots=\frac{\pi^4}{90}$
この結果は⑨と一致する．

$x=-2\sum_{n=1}^{\infty}\frac{\cos n\pi}{n}\sin nx$ →[1]
$x^3=\sum_{n=1}^{\infty}\left(-\frac{2\pi^2\cos n\pi}{n}+\frac{12\cos n\pi}{n^3}\right)\sin nx$ →[5]
$f(x)=x,\hspace{5}g(x)=x^3$ として(11.4)を適用すると
$\frac{1}{\pi}\int_{-\pi}^{\pi}x\cdot x^3dx=\sum_{n=1}^{\infty}(-2\cos n\pi)\left(-\frac{2\pi^2\cos n\pi}{n}+\frac{12\cos n\pi}{n^3}\right)$
$\frac{2\pi^4}{5}=-2\{-(2\pi^2-12)+\frac{1}{2}(-\frac{2\pi^2}{2}+\frac{12}{2^3})$
$+\frac{-1}{3}(-\frac{2\pi^2}{3}+\frac{-12}{3^3})+\frac{1}{4}(-\frac{2\pi^2}{4}+\frac{12}{4^3})+\cdots\}$
$-\frac{\pi^4}{5}=-2\pi^2(1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots)+ 12(1+\frac{1}{2^4}+\frac{1}{3^4}+\cdots)$
ここで
$\frac{1}{1^2}+ \frac{1}{2^2}+ \frac{1}{3^2}+\cdots=\frac{\pi^2}{6}$
の結果を使い，
$1+\frac{1}{2^4}+\frac{1}{3^4}+\cdots=S$
とおくと
$-\frac{\pi^4}{5}=-2\pi^2\cdot\frac{\pi^2}{6}+ 12S$
$\frac{2\pi^4}{15}=12S$
$S=\frac{\pi^4}{90}$
したがって
$\frac{1}{1^4}+ \frac{1}{2^4}+ \frac{1}{3^4}+ \cdots=\frac{\pi^4}{90}$

$x^3=\sum_{n=1}^{\infty}\left(-\frac{2\pi^2\cos n\pi}{n}+\frac{12\cos n\pi}{n^3}\right)\sin nx$ →[5]
に対してパーセバルの等式を適用すると
$\frac{1}{\pi}\int_{-\pi}^{\pi}x^6dx=(2\pi^2-12)^2+(-\frac{2\pi^2}{2}+\frac{12}{2^3})^2$
$+(\frac{2\pi^2}{3}-\frac{12}{3^3})^2+(-\frac{2\pi^2}{4}+\frac{12}{4^3})^2+\cdots$
$\frac{2\pi^6}{7}=4\pi^4(1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots)$
$+ 12^2(1+\frac{1}{2^6}+\frac{1}{3^6}+\frac{1}{4^6}+\cdots)$
$-4\pi^2\times 12(1+\frac{1}{2^4}+\frac{1}{3^4}+\frac{1}{4^4}+\cdots)$
$\frac{1}{1^2}+ \frac{1}{2^2}+ \frac{1}{3^2}+\cdots=\frac{\pi^2}{6}$
$\frac{1}{1^4}+ \frac{1}{2^4}+ \frac{1}{3^4}+\cdots=\frac{\pi^4}{90}$
の結果を使い，
$1+\frac{1}{2^6}+\frac{1}{3^6}+\cdots=S$
とおくと
$\frac{2\pi^6}{7}=4\pi^4\cdot\frac{\pi^2}{6}+ 12^2S-48\pi^2\cdot\frac{\pi^4}{90}$
$(\frac{2}{7}-\frac{2}{3}+\frac{8}{15})\pi^6=12^2S$
$S=\frac{\pi^6}{945}$
したがって
$1+\frac{1}{2^6}+\frac{1}{3^6}+\cdots=\frac{\pi^6}{945}$

$x^2=\frac{\pi^2}{3}+ 4\sum_{n=1}^{\infty}\frac{\cos n\pi}{n^2}$ →[4]
$x^4=\frac{\pi^4}{5}+\sum_{n=1}^{\infty}\frac{8}{n^2}\left(\pi^2-\frac{6}{n^2}\right)\cos n\pi\cos nx$ →[6]
$f(x)=x^2,\hspace{5}g(x)=x^4$ として(11.4)を適用すると
$\frac{a_0}{2}=\frac{pi^2}{3}\rightarrow a_0=\frac{2\pi^2}{2},\hspace{5}\frac{c_0}{2}=\frac{\pi^4}{5}\rightarrow c_0=\frac{2\pi^4}{5}$
$\frac{a_0c_0}{2}=\frac{2\pi^6}{15}$
$\frac{1}{\pi}\int_{-\pi}^{\pi}x^2\cdot x^4dx=\frac{2\pi^6}{15}+ 4\cdot\frac{1}{1}\cdot\frac{8}{1^2}(\pi^2-\frac{6}{1})$ $+ 4\cdot\frac{1}{2^1}\cdot\frac{8}{2^2}(\pi^2-\frac{6}{2^2})$
$+ 4\cdot\frac{1}{3^1}\cdot\frac{8}{3^2}(\pi^2-\frac{6}{3^2})+\cdots$
$\frac{2\pi^6}{7}=\frac{2\pi^6}{15}+ 32\pi^2(1+\frac{1}{2^4}+\frac{1}{3^4}+\cdots)$
$-36\times 6(1+\frac{1}{2^6}+\frac{1}{3^6}+\cdots)$

$\frac{1}{1^4}+ \frac{1}{2^4}+ \frac{1}{3^4}+\cdots=\frac{\pi^4}{90}$
の結果を使い，
$1+\frac{1}{2^6}+\frac{1}{3^6}+\cdots=S$
とおくと
$\frac{2\pi^6}{7}-\frac{2\pi^6}{15}=32\pi^2\cdot\frac{\pi^4}{90}-32\times 6S$
$\frac{16\pi^6}{105}-\frac{16\pi^6}{45}=-32\times 6S$
$\frac{\pi^6}{105}-\frac{\pi^6}{45}=-12S$
$-\frac{4\pi^6}{315}=-12S$
$S=\frac{\pi^6}{945}$
したがって
$1+\frac{1}{2^6}+\frac{1}{3^6}+\cdots=\frac{\pi^6}{945}$

〇== メニューに戻る　

..高卒～大学数学のメニューに戻る

■このサイト内のGoogle検索■

△このページの先頭に戻る△【アンケート送信】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．

○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）

質問に対する回答の中学版はこの頁，高校版はこの頁にあります