→ スマホ用は別頁
|
1. 1変数--高階導関数を用いた極値の判別(1)
1変数関数の場合,点(a, b)における第n次導関数の符号と極値の判別を振りかえってみると,次のようになっている.(高校数学Ⅲの内容)
ウ)については「分からない」「判断できない」と述べているのではなく「第2次導関数までの材料だけでは,判断できないということで,第3次以上の導関数も調べれば判断できます.」 |
① f’(a)=0, f”(a)=0, f(3)(a)>0のとき
次の表において,(B)(E)(H)が分かっているときに,表の残りの部分を埋めて,最終的に(J)(L)を見て,極値かどうか判断します.
下に文章で書いている考え方に慣れてください
f(x)が第3次導関数まで連続微分可能とすると,
f(3)(a)>0のとき,x=aの近傍でf(3)(a)は連続だから,急に符号が変わることはなく,(G)の符号が+だと分かる.同様にして,(I)の符号も+だと分かる. (E)においてf”(a)=0であるが,その導関数f(3)(x)の符号は,x>aのとき,(I)により正だから,f”(x)はx=aのとき0で,xが増加するとそれよりも増えるのだから,(F)の符号は正になる. 逆に,(G)によりx<aのとき,f(3)(x)の符号は正で,(E)においてf”(a)=0となるのだから「f”(x)は増えて0になる.」したがって,それまでは負だったことになり,(D)の符号は負になる. 同様にして,(B)においてf’(x)=0で,その導関数が(F)において正だから,f’(x)は0から増え,(C)の符号は正になる.逆に,(D)においてf”(x)が負で,(B)においてf’(x)=0となるのだから,f’(x)は減って0になることになり,それまでの(A)は正 (A)(C)の符号を見ると,(J)(L)において増加であることになり,x=aにおいてf(x)は極値とならない. |
||||||||||||||||||||||||||||||||
|
② f’(a)=0, f”(a)=0, f(3)(a)<0のとき
ほぼ①と同様の考え方で,次の表が埋まります.これにより,x=aにおいてf(x)は極値とならない.
|
③ f’(a)=0, f”(a)=0, f(3)(a)=0, f(4)(a)>0のとき
ほぼ同様の考え方で,次の表が埋まります.これにより,x=aにおいてf(x)は極小値となる.
|
|
④ f’(a)=0, f”(a)=0, f(3)(a)=0, f(4)(a)<0のとき
ほぼ同様の考え方で,次の表が埋まります.これにより,x=aにおいてf(x)は極大値となる.
|
さらに,第4次以上の導関数f(n)(a)=0の場合も,同様にして表を組み立てて行けば極値か否かを判断できる. 一般に次のことが言える. (1) a<xのときの導関数の符号はすべて同じになる. (2) x<aのときの導関数の符号は交互に変わる. (3) (1)(2)より,nが奇数のとき,f(k)(a)=0(1≦k<n),f(n)(a)>0, f(n)(a)<0のとき,f(a)は極値にならない. (4) (1)(2)より,nが偶数のとき,f(k)(a)=0(1≦k<n),f(n)(a)>0のとき,f(a)は極小値になり,f(k)(a)=0(1≦k<n),f(n)(a)<0のとき,f(a)は極大値になる. |
|
2. 1変数--高階導関数を用いた極値の判別(2)
高階導関数を用いて極値を判別する方法は,テイラー展開を利用して次のように書くこともできる.2回まで連続微分可能な関数f(x)があるとき,テイラーの定理により,次の形に書ける. (ただし,cはaとxの間の数)
(3.1)
(解説)(3.2) (3.1)← ここで
関数f”(x)は連続だから,連続の定義によって
以上により,どんな小さな正の値εを与えられても,適当な正の数δを選べば |c−a|<δ → |f”(c)−f”(a)|<ε が成り立つ.すなわち |c−a|<δ → f”(a)−ε<f”(c)<f”(a)+ε であるから (0<)ε<f”(a):f”(a)よりも小さな(正の数)εに対してはf”(c)>0となる (3.2)← 同様にして, においてf”(c)<0から, |
3回まで連続微分可能な関数f(x)があるとき,テイラーの定理により,次の形に書ける. (ただし,cはaとxの間の数)
(3.3)
(解説)(3.4) (3.3)← ここで
証明は(3.1)と同様
ここで,よって, (3.4)← (3.3)と同様にして示される 以下同様にして示される.(証明略)
(3.7)
(3.8) |
|
3. 2変数関数における極値の定義
2変数の関数f(x, y)について,点(a, b)の近くの任意の点(x, y)に対して
(x, y)≠(a, b)ならばf(x, y)<f(a, b)
が成り立つとき,f(x, y)は,点(a, b)で極大であるといい,f(a, b)を極大値という. 
(x, y)≠(a, b)ならばf(x, y)>f(a, b)
が成り立つとき,f(x, y)は,点(a, b)で極小であるといい,f(a, b)を極小値という.  |
道路が山脈を横切るような場合,一番低い所で越える方が楽なので,道路は次の図で「峠」と書いた場所を横切ることが多い.
道路に沿って移動する限り,峠は一番高い箇所になる. これに対して,山の稜線に沿って移動する場合,峠は一番低い場所になる.(山岳用語で,この地形を「コル」という.もっとはっきりと「サカサマ峠」という地名になっている場合もある.) 地形で峠やコルと呼ばれる形は,数学用語では  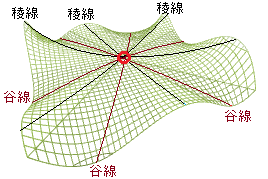 |
|
4. 2変数関数における極値の判別
【2変数関数が極値をとるための必要条件】
偏微分可能な関数  (解説)
(解説)極大値となるためには,yを固定して,xだけを変化させたときにも,点(a, b)において極大でなければならないから, 同様にして,xを固定して,yだけを変化させたときにも,点(a, b)において極大でなければならないから, 極小値についても同様
※前述の鞍点もこの条件①を満たすことから分かるように,①を満たすだけで極値になるとは言えない.①は極値をとるための必要条件であって,十分条件は別途検討しなければならない.
|
【2変数関数が極値をとるための十分条件】
関数 とおくと (1) ⅰ) ⅱ)
ⅰ)ⅱ)で
(2)(3)
判別に用いる式は,教科書によって,著者によって異なる
[A] 2次方程式の判別式に類似する形で上記のように
の2種類がある.出版物では[B]の流儀がやや多いようであるが,符号が逆になっているということに気を付ければよく,他に内容的な違いはない.で定義する教科書と [B] ヘッセ行列式[ヘッシアン]で定義する形 |
|
(解説) 2変数関数のテイラーの定理により いま, [Ⅰ] この式の右辺は,  判別式が負,すなわち
判別式が負,すなわちそのうち,2次の係数が正のものは①のグラフになるから よって (1) ⅰ)
つねに
ⅱ)すなわち となって,
つねに
すなわち となって,
ⅰ)ⅱ)で
(無理して両方使う必要はないが, |
(2) すなわち
例えば,
[Ⅱ] だから, であるから, また, だから, であるから, |
|
5. 問題
【例5.1】
(解答)より, このとき により,点 極小値は, 
(参考)
この問題を「高校数学Ⅰ」の問題として「平方完成の変形によって」解く場合の答案 (1) はじめに\(\color{red}{x}\)だけを文字として[\(y\)と数字を係数と見なして]平方完成する \( \displaystyle f(x,\hspace{2px}y)=\textcolor{red}{x^2}-\textcolor{red}{x}y+ y^2+2\textcolor{red}{x}-7y+ 5 \) \( \displaystyle =\textcolor{red}{x^2}+(-y+2)\textcolor{red}{x}-7y+ 5 \) \( \displaystyle =\{\textcolor{red}{x}+\frac{-y+2}{2}\}^2-(\frac{-y+2}{2})^2+y^2-7y+ 5 \) \( \displaystyle =\{\textcolor{red}{x}+\frac{-y+2}{2}\}^2-\frac{y^2}{4}+y-1+y^2-7y+ 5 \) \( \displaystyle =\{\textcolor{red}{x}+\frac{-y+2}{2}\}^2+\frac{3}{4}y^2-6y+ 4 \) (2) 次に,残りの項を\(y\)について平方完成する \( \displaystyle =\{\textcolor{red}{x}+\frac{-y+2}{2}\}^2+\frac{3}{4}(y^2-8y)+ 4 \) \( \displaystyle =\{\textcolor{red}{x}+\frac{-y+2}{2}\}^2+\frac{3}{4}\{(y-4)^2-16\}+ 4 \) \( \displaystyle =\{\textcolor{red}{x}+\frac{-y+2}{2}\}^2+\frac{3}{4}(y-4)^2-8 \) これより \( \displaystyle {\Bigg\lbrace}\begin{array}{l} x+\dfrac{-y+2}{2}=0\\ y-4=0 \end{array}\leftrightarrow {\Big\lbrace}\begin{array}{l} x=1\\ y=4 \end{array}\) のとき,極小値かつ最小値\(-8\)をとる |
【例5.2】
(解答)より, このとき よって,極値なし.  |
|
【例5.3】
(解答)より ① だから, ② だから,  |
【例5.4】
(解答)より ① だから, ② だから, ③ だから, ④ だから, 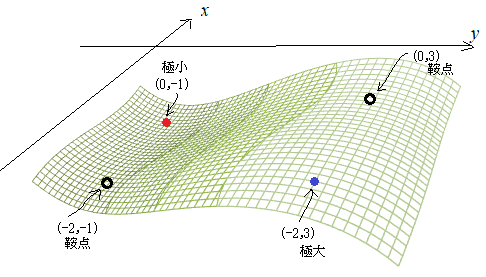 |
|
【例5.5】
(解答)より |
① だから, ② だから, ③ だから, ④ だから,  |
|
6. 条件付極値問題
ここまでに扱ったのは,次のような形で,2つの変数を高校数学に登場する簡単な例を使って,条件付の極値問題の解き方を振り返ってみる. 【例1】 |
(解き方の要点)------
①により,2変数
(答案)------そこで,この1変数になった関数
(A) (B)
 |
|
【例2】
■強いて
ここで,手順を見直して,次の表のイメージで「微分してから,代入する」ことを考える.■条件式が円を表す場合には, ■高校では,②を=kとおいて,①に代入することにより,実数条件を判別式で求めるという方法もよく用いられるが,その方法は①が2次関数である場合に限られる.だから,ここではこれも採用しない.
|
①の両辺を ②の両辺を ①’より ア) ②’に代入 ゆえに
①より
 |
|
以上の解き方を一般化すると,次のようになる. ②の両辺を
[式1]
|
①’より ①’を②’に代入すると,②が極値となる点では,次の関係が成り立つ. さらに, すなわち,次の連立方程式を満たすものが求める極値である.
[式2]
|
|
7. ラグランジュの未定乗数法
6.で述べた解き方は,さらに次の「ラグランジュの未定乗数法」と呼ばれる形にまとめられることが多い.まず,6.③の比例形条件式は1つの定数を使って2つの式に分けることができる.
[式3]
(注:さらに,これら3つの式は,次の形の1つの関数 |
この式の
[式4]
(解説)これら(ⅰ)(ⅱ)(ⅲ)が上記の(1)(2)(3)に等しいことを思いつくのは大変であるが[ラグランジュに感謝するほかない!],これらが等しいことは簡単に証明できる.
(ⅱ)⇔
※①③もしくは(1)(2)(3)が2変数の条件付き極値問題であるのに対して,ラグランジュの未定乗数法(ⅰ)(ⅱ)(ⅲ)はこれを3変数の条件なし極値問題に書き換えていると見ることもできる.
(ⅲ)⇔ (ⅰ)⇔ |
|
8. 問題
■解き方も結果も別ルートで確認できる,高校数学Ⅰレベルの問題で,解き方を確かめてみる■
【例1.1】
[式1]の方法で解いてみる(解答) ①を②に代入する を解くと,極値となるための必要条件[停留点:極値の候補]は,
このとき |
■解き方も結果も別ルートで確認できる,高校数学Ⅰレベルの問題で,解き方を確かめてみる■
【例8.1】
[式4]ラグランジュの未定乗数法で解く(解答) ア)
(1)(2)より
イ)⇒ (1)が成り立たないから,極値でない ⇒ (2)が成り立たないから,極値でない 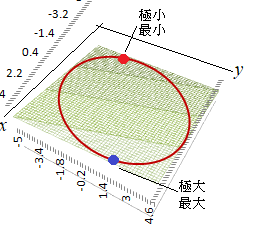 |
|
【例8.2】
[式1]の方法で解いてみる(解答) ア) ①を③に代入 1) ⇒極小かつ最小 2) ⇒極大かつ最大 ⇒極値でない(最大でも最小でもない) ※  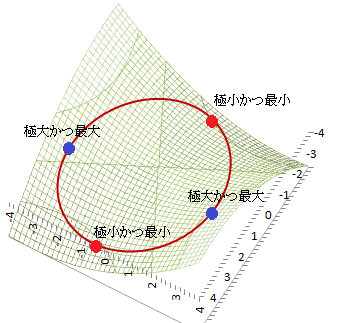 「x^2+ y^2=10 のとき, z=-4x^2+ 6xy+ 4y^2 の最大値,最小値を求めてください.」
|
【例8.3】
上記の[式4]ラグランジュの未定乗数法で解く(解答) ア)
(1)(2)より
イ)その1) その2)
上記のア)その1)と同じ結果になる
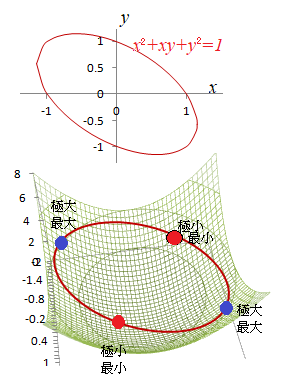 [式1]の方法で 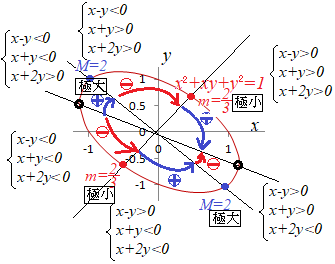 |
|
【例8.4】
[式1]の方法で解く(解答) ア) ①を③に代入 その1) ①に代入すると その2) ①に代入すると
\(x^2-xy+ y^2=1\)に代入すると
\(4y^2-2y^2+ y^2=1\) \(3y^2=1\) \(\displaystyle y=\pm\frac{1}{\sqrt{3}}\) ⇒極値でない   「x^2-xy+ y^2=1 のとき, z=x^2+ y^2 の最大値,最小値を求めてください.」
|
 ラグランジュの未定乗数法の説明をすると言いながら,[式1]の原始的な方法で説明しているじゃないか!この教材の作者は「裏切者か?」
ラグランジュの未定乗数法の説明をすると言いながら,[式1]の原始的な方法で説明しているじゃないか!この教材の作者は「裏切者か?」 増減表の説明には[式1]の原始的な方法が教えやすので,そちらでやっています.他方では,学生がラグランジュの未定乗数法の問題を出されたときに困らないように,そちらの説明もしています.
増減表の説明には[式1]の原始的な方法が教えやすので,そちらでやっています.他方では,学生がラグランジュの未定乗数法の問題を出されたときに困らないように,そちらの説明もしています.解き方は1つでなければならないなどと狭く絞るのでなく,解き方は幾つもあると考えてください.
【例8.5】
[式1]の方法で解く(解答) ア) ①を③に代入 その1) (#1)に代入すると ⇒極大かつ最大 その2) (#1)に代入すると ⇒極小かつ最小
(#1)に代入 ⇒極値でない 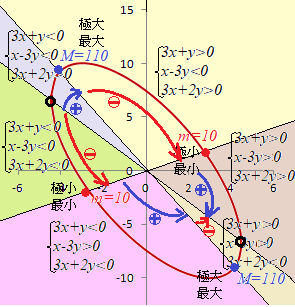  「5x^2+ 3xy+ y^2=55 のとき, z=x^2+ y^2の最大値,最小値を求めてください.」
|