�@�Ȃ��C
 \( \displaystyle e^{-st} \)
\( \displaystyle e^{-st} \)���|����̂��ɂ��ẮC���������̐����D
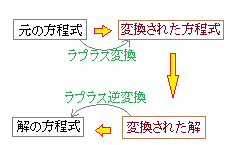
�@���v���X�ϊ�
=\int_{0}^{\infty}f(t)e^{-st}dt\]&chco=aa4422) \( \displaystyle X(s)=\int_{0}^{\infty}f(t)e^{-st}dt \)
\( \displaystyle X(s)=\int_{0}^{\infty}f(t)e^{-st}dt \)
���������邽�߂ɂ́C���̔�ϕ����̋Ɍ��l���O�łȂ���Ȃ�Ȃ��D
e^{-st}=0\]&chco=aa4422) \( \displaystyle \lim_{t\rightarrow\infty}f(t)e^{-st}=0 \)
\( \displaystyle \lim_{t\rightarrow\infty}f(t)e^{-st}=0 \)
�@���������łȂ���C���Ƃ��ΐ��̒l
&chco=aa4422) \( \displaystyle a\hspace{3px}(\gt 0) \)
\( \displaystyle a\hspace{3px}(\gt 0) \)�Ɏ�������̂Ȃ�C�\���傫��
 \( \displaystyle t=t_0 \)
\( \displaystyle t=t_0 \)�̒l�ɑ��āC��ϕ����́C�ق�
 \( \displaystyle a \)
\( \displaystyle a \)�ɓ���������C��L�̐ϕ���
&chco=aa4422) \( \displaystyle a\times(\infty-t_0) \)
\( \displaystyle a\times(\infty-t_0) \)�����傫���Ȃ��āC�������Ȃ��D��ϕ��������̒l�Ɏ�������Ƃ����C���l�ɂ��Đϕ��͕��̖�����ƂȂ�C�������Ȃ��D
�@���ǁC���v���X�ϊ����������邽�߂ɂ́C��ϕ����̋Ɍ��l���O�ɂȂ邱�Ƃ��K�v�����ł���D
�@���ϕ��łƂĂ��悢����������̂��w�����ł��邪�C���Ƃ���
=1&chco=aa4422) \( \displaystyle f(t)=1 \)
\( \displaystyle f(t)=1 \)�̂悤�ȊȒP�Ȋ����l���Ă݂�ƁC
&chco=aa4422) \( \displaystyle K(s,t) \)
\( \displaystyle K(s,t) \)�Ƃ���
 \( \displaystyle e^{st} \)
\( \displaystyle e^{st} \)���g����
=\int_{0}^{\infty}e^{st}dt\]&chco=aa4422) \( \displaystyle X(s)=\int_{0}^{\infty}e^{st}dt \)
\( \displaystyle X(s)=\int_{0}^{\infty}e^{st}dt \)
�͔��U���Ă��܂��D�w�����̓��ŁC
 \( \displaystyle t\rightarrow\infty \)
\( \displaystyle t\rightarrow\infty \)�̂Ƃ��C�O�Ɏ�������̂�
 \( \displaystyle e^{-st} \)
\( \displaystyle e^{-st} \)�ł���D
�@�܂��C���̊���
 \( \displaystyle t\lt 0 \)
\( \displaystyle t\lt 0 \)�̂Ƃ��C�}���ɑ傫���Ȃ邩��C���v���X�ϊ������������邽�߂ɂ́C�ϕ���ԂƂ���
 \( \displaystyle t\gt 0 \)
\( \displaystyle t\gt 0 \)�̋�Ԃ������g���D
�@���ǁC
 \( \displaystyle t\gt 0 \)
\( \displaystyle t\gt 0 \)�̋�ԂŃ��v���X�ϊ��̐ϕ������������邽�߂ɁC�}����0�Ɏ��������
 \( \displaystyle e^{-st} \)
\( \displaystyle e^{-st} \)���g���Ă���Ɖ��߂ł���D
5. �悭�g�����v���X�ϊ��Ƃ��̏ؖ�