 (1) �O�p��̒�`
(1) �O�p��̒�`
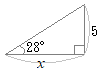
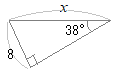
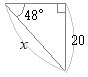
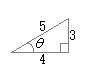
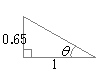
�@�E�}�̂悤�Ȓ��p�O�p�`�ł́C�ӂ̒����̔�ɂ���ĎO�p��̒l����`����Ă��܂��D
(2) ���p�O�p�`�̕ӂ̒���
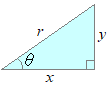
�@�t�ɏ�L�̎��@�ɂ����āCsinθ��r�̒l���������Ă���Ƃ��Cy�̒l�͎��̂悤�ɂ��ċ��߂��܂��D
y=r sinθ…�C �@���l�ɂ��āC���A�ɂ����āCcosθ��r�̒l���������Ă���Ƃ��Cx�̒l�͎��̂悤�ɂ��ċ��߂��܂��D x=r cosθ…�D �@����ɁC���B�ɂ����āCtanθ��x�̒l���������Ă���Ƃ��Cy�̒l�͎��̂悤�ɂ��ċ��߂��܂��D y=x tanθ…�E
�� ���̂悤�ɂ��āC�O�p��̒lsinθ, cosθ, tanθ�����炩���ߕ������Ă���ꍇ�ɂ́C�����C�D�E�̎����g���āC�ӂ̒��������߂邱�Ƃ��ł��܂��D
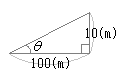
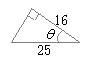
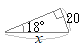
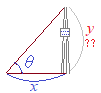 �@�Ⴆ�C�E�}�̂悤�ȍ������̍������ڑ���͓̂�����Ƃł����C�p�x�ƂƉ��̒����𑪂�C�v�Z�ɂ���ē��̍��������߂邱�Ƃ��ł��܂��D���̂悤�ȕ��@�͎O�p���ʂƌĂ�܂��D
�@�Ⴆ�C�E�}�̂悤�ȍ������̍������ڑ���͓̂�����Ƃł����C�p�x�ƂƉ��̒����𑪂�C�v�Z�ɂ���ē��̍��������߂邱�Ƃ��ł��܂��D���̂悤�ȕ��@�͎O�p���ʂƌĂ�܂��D
|
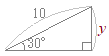
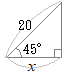
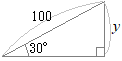
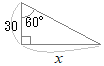
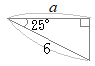
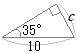
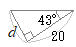
 �i�j
�i�j