第一象限や第二象限がよくわかりません。どのような時にどんな象限がきまり、それに対する答えがどうなっていくのかを教えていただきたいです
 =>[作者]:
=>[作者]:連絡ありがとう.この教材の管理人(私)は,第1象限などの用語は中学校1年生で習って,その後自由に使いこなしていると思っていましたが,今の教科書を見ると,中学校の教科書には登場しないようです.
象限という用語を使わないと,反比例のグラフが「どこ」と「どこ」にあるというようなことが言えなくなって不便だと思うのですが,そういう場所を表す用語はないらしい.
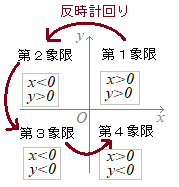
象限という用語は,高校数学Ⅰで初登場のようです.左図のように,
x, yとも正の場所を「第1象限」といい,以下反時計回り(左回りに)第2象限,第3象限,第4象限とします.ただし,座標軸上はどの象限にも入れません.
三角関数との関係で言えば,象限ということを意識しないと,符号の決め方が分からなくなるはずです.
例えば,

において
x, yは象限に応じて決まる符号が付いていて(符号付の実数),
rだけは半径(長さ,符号なしの実数)なので常に正です.
だから,第1象限では

第2象限では

のように各象限に応じて三角関数の符号が決まります.[まずこれが重要]
逆に,三角関数の符号が決まれば,象限が決まる場合と決めきれない場合があります.
例えば,

という条件だけでは,第3象限と第4象限の可能性があってどちらと決められませんが,さらに,

という条件もついていると,第3象限に決まります.
今学習しているところ、効率よく学習をする上でのポイントをしっかり書いてあって、分かりやすく説明しているのでとてもいいと思います。
問題も○×がすぐわかり、解説もしてくれるので、とてもいいです。
これからも利用させていただきます。
=>[作者]:連絡ありがとう.問題をやり,必要に応じて解説に立ち返る学習方法は,このサイトの一番良い利用方法だと考えています.
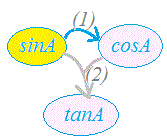 ○ 例えば、
○ 例えば、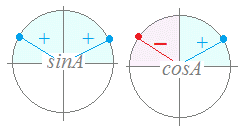
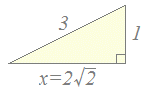 注意
注意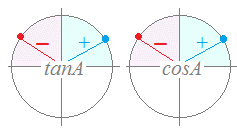
 =>[作者]:連絡ありがとう.この教材の管理人(私)は,第1象限などの用語は中学校1年生で習って,その後自由に使いこなしていると思っていましたが,今の教科書を見ると,中学校の教科書には登場しないようです.
=>[作者]:連絡ありがとう.この教材の管理人(私)は,第1象限などの用語は中学校1年生で習って,その後自由に使いこなしていると思っていましたが,今の教科書を見ると,中学校の教科書には登場しないようです.