|
■解説■
○ 高校数学Ｉで登場する「三角比の相互関係」とは、次の２つの公式のことです。 sin2A+cos2A=1 …(1) tanA = …(2)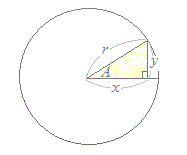 
(1)の証明：x2+y2=r2の両辺をr2で割ると ( )2+( )2=1 ここで=cosA , =sinAだから (1)が得られる。 (2)の証明： tanA = , sinA = , cosA = だから = = · = = tanA 三角比sinA , cosA , tanAのうち１つ分かれば、残りはこれらの公式を使って「芋づる式に」求まります。 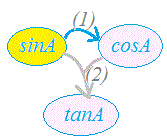 ○ 例えば、sinAが分かれば(1)を使ってcosAが求まり、さらに(2)を使ってtanAが求まります。しかし、例えばtanA = のように、三角比のうちでtanAだけが与えられて残りのsinA , cosAを求めるときは要注意です。 (2)からsinA=3 , cosA=4などと間違う生徒が多いからです。（−1≦sinA , cosA≦1を満たしていないものは、三角比になりません。ここでは、比だけが与えられている場合には、 ：、 ：、 … ： などの可能性も考えなければなりません。 正しいのは、：または：になります．） このように、tanA ⇒ cosA（またはsinA）の関係式が必要なときは、(1)の両辺をcos2A（またはsin2A）で割って次の公式(3)(4)を「その場で作ればよい」。（「公式」を覚えるのでなく、必要になったときに作るようにします･･･「公式がある」ということだけを覚えておく…覚えなければならない公式の数を減らして、公式間の関連をつかむようにする）
tan2A+1 = …(3)
1+ = …(4)
(3)の証明：
sin2A+cos2A=1の両辺をcos2Aで割ると +1= ここで(2)を用いて左辺を変形すると tan2A+1 = (4)の証明： (3)と同様にして両辺をsin2Aで割ります。 このとき、 tanA= → = = に注意します。 |
| 《問題》 次の左欄の式に等しいものを下欄の選択肢から選んでください． |
|
|
(携帯版)...メニューに戻る