|
【例1】
0°≦θ≦180°のとき,次の三角不等式を解きなさい. 2cos2θ> 1+cosθ
(解答)
2cos2θ−cosθ−1>0 この式の左辺を因数分解する
2x2−x−1>0の左辺をたすき掛け因数分解すると
(2cosθ+1)(cosθ−1)>0(2x+1)(x−1)>0となります. 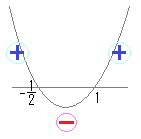 2次不等式(2x+1)(x−1)>0の解は,
2次不等式(2x+1)(x−1)>0の解は,2次方程式(2x+1)(x−1)=0の解の「両側」です. すなわち 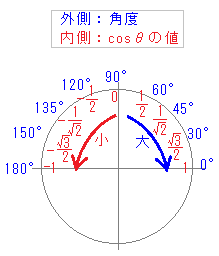
またはcosθ>1 0°≦θ≦180°のとき, (1) (2) cosθ>1を満たす角度はない. 以上より, 120°<θ≦180°…(答)
以下の問題では,各自で計算用紙を使って計算してから,下の選択肢のうちで正しいものをクリックしてください.(暗算では無理でしょう)
【問題1】
0°≦θ≦180°のとき,次の不等式を解きなさい. 2sin2θ+3sinθ−2<0
因数分解して(2sinθ−1)(sinθ+2)<0…(1)と変形します.
2次方程式
(x+2)(2x−1)=0 の解 の「間」は  (1)の解は
(1)の解は0°≦θ≦180°のとき,右図のように0≦sinθ≦1だから 実際には を解く.(sinθ=0は合格) 0°≦θ<30°, 150°<θ≦180°…(答)
【問題2】
0°≦θ≦180°のとき,次の不等式を解きなさい.
因数分解して
2次方程式
の解 の「両側」は 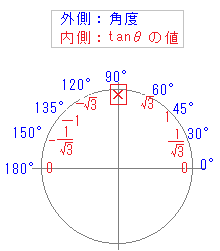 (1)の解は
(1)の解は0°≦θ≦180°のとき,右図の値をとる ※θ=90°のときtanθは定義されないので注意 ※また,90°<θ<180°のとき,tanθ<0となることに注意 (1) 60°<θ<90° (2) tanθ<0を満たす角度は 90°<θ<180° 以上より60°<θ<90°,90°<θ<180°…(答) |
