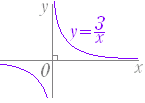
※ 双曲線の方程式は,中学校で反比例のグラフ ■ c>a>0 , b>0 のとき,方程式
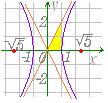
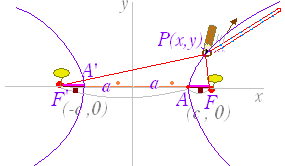
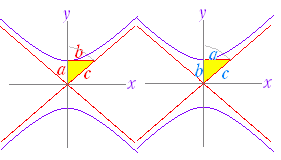
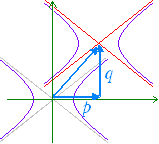
−=1 …(1) で表わされる曲線は,図1のような双曲線になる. 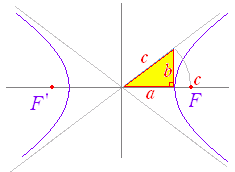 ○ この曲線は「2定点 F( , 0) , F’(− , 0) からの距離の差が一定 2a である点の軌跡」となっている.(解説は次の項目↓) ○ 2点 F( , 0) , F’(− , 0) を双曲線の焦点という. ○ 点 A(a , 0) , A’(−a, 0) を頂点という. ○ 2つの焦点の中点を双曲線の中心という.(1)の双曲線の中心は原点 O( 0 , 0 ) にある. ○ (1)の双曲線は x 軸,y 軸,中心に関して対称となっている. ○ x が限りなく大きくなるとき,双曲線は 直線 y=±x に限りなく近づく.この直線を双曲線の漸近線という.漸近線は2つある. (漸近線の方程式は(1)の右辺を 0 に変えて,左辺を因数分解したものになっている. −=0 ←→(+)(−)=0 ←→y=−x , y=x ■ −=−1 は,図2のような双曲線になる. 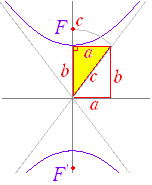 F(0 , ) , F’(0 , − ) また,主軸は y軸上にあり,頂点の座標は B(0 , b) , B’( 0 ,−b) になる. |
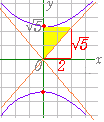
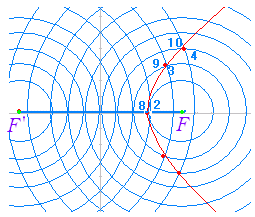
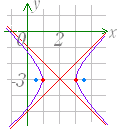
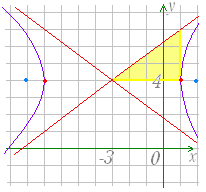
| 《基本事項のチェック》 −=1 は,図3のような形の双曲線で, 焦点の座標は F(5 , 0) , F’(−5 , 0), 頂点の座標は (4 , 0) , (−4 , 0) 中心の座標は (0 , 0) である. 双曲線の任意の1点を P とするとき,|FP−F’P|=8 となる. 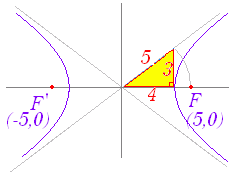 |
 移動後の方程式は
移動後の方程式は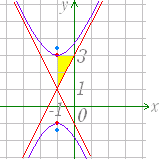
 =>[作者]:連絡ありがとう.
=>[作者]:連絡ありがとう.