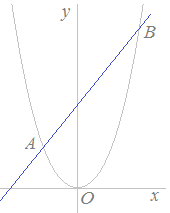
 【例1】 【例1】y=x2のグラフ上に2点A,Bがあります.A,Bのx座標がそれぞれ−1, 3であるとき,次の問いに答えなさい. (1)2点A,Bの座標を求めなさい. (2)2点A,Bを通る直線の方程式を求めなさい. (3)2点A,Bを通る直線がy軸と交わる点Pの座標を求めなさい. (4)△POBの面積を求めなさい. (1)
x=−1をy=x2に代入するとy=(−1)2=1となるから,点Aの座標は(−1, 1)…(答)
(2)x=3をy=x2に代入するとy=32=9となるから,点Bの座標は(3, 9)…(答)
求める直線の方程式をy=ax+b…(A)とおくと,
(3)点A(−1, 1)がこの直線上にあるから, 1=−a+b…(B) また,点B(3, 9)がこの直線上にあるから, 9=3a+b…(C) (B)(C)を係数a, bを求めるための連立方程式として解く. 1=−a+b…(B) −)9=3a+b…(C) −8=−4a a=2…(D) (D)を(B)に代入 b=3 (A)にこれらa, bの値を代入すると y=2x+3…(答)
y=2x+3の方程式にx=0に代入するとy=3となるから,点Pの座標は(0, 3)…(答)
(4)
△POBにおいてPOを底辺と見ると,底辺の長さは3.このとき,高さはBのx座標3になるから,△POBの面積は
(底辺)×(高さ)÷2=…(答) |
 【問1】 【問1】y=2x2のグラフ上に2点A,Bがあります.A,Bのx座標がそれぞれ−1, 2であるとき,次の問いに答えなさい. (1)2点A,Bの座標を求めなさい. (2)2点A,Bを通る直線の方程式を求めなさい. (3)2点A,Bを通る直線がy軸と交わる点Pの座標を求めなさい. (4)△AOPの面積を求めなさい. |
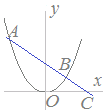 右図のように2次関数
右図のように2次関数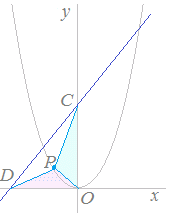 右図のように2次関数
右図のように2次関数