|
現在地と前後の項目 積の導関数/商,分数関数の導関数/合成関数の導関数/媒介変数表示の導関数/無理関数と分数指数(復習)/無理関数の導関数/陰関数の導関数/重要な極限値(sinx/x)/三角関数の導関数1/三角関数の導関数2/指数，対数関数の導関数/対数微分法/いろいろな関数の導関数/極大値，極小値/漸近線の方程式1/漸近線の方程式2/凹凸と変曲点/増減.極値/凹凸.変曲点/漸近線/グラフ(1)/分数関数の漸近線/グラフ(2)/グラフの概形と漸近線（一覧）/媒介変数表示…接線.法線.速度/媒介変数表示とx,y方向の変化/ ※この頁では漸近線の方程式の求め方を解説します．
(1)縦方向の（x軸に垂直な）漸近線
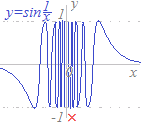
【例1-1】有限の値aに対して，x→aのときy→∞またはy→−∞になるとき，x=aが漸近線になります． y=  1x−1の関数において，x=1のときは分母が0となって関数が定義されず，x→1のときy→±∞となります．このとき，x=1が漸近線になります．（図１．ただし，図１にはもう一つ横向きの（x軸に平行な）漸近線もありますが，これについては(2)で解説します．） 【例1-2】 y=tanxにおけるx= π2，y=logxにおけるx=0のように分母が明示されていなくてもx→aのときy→∞またはy→−∞になることがあります．このとき，各々x=  π2，x=0が漸近線になります．（図２，図３）図３において，x<0のときy=logxは定義されませんが，x>0の様子からx=0が漸近線です． 【例1-*】 y=e 1xにおいてx→+0のとき1x→+∞だからy→+∞，これに対してx→−0のとき 1x→−∞だからy→e−∞=0したがって，x→+0のときは漸近線ができますが，x→−0のときは漸近線はできません．この場合でも，x→+0のときからx=0が漸近線です．（図４） 【例1-**】 y=sin 1xにおいてx→0のとき1x→±∞ですがy→±∞ではないのでx=0は漸近線ではありません．（この関数はx=0の付近で激しく震動し，x=0のとき関数が定義されません．）（図５．図５には横向きの（x軸に平行な）漸近線がありますが，これについては(2)で解説します．）
|
|
|
(2)横方向の（x軸に平行な）漸近線
x→+∞のときとx→−∞のときを各々考えることができ，
x→±∞のときy→a（aは有限確定の値）になるとき，y=aが漸近線になります．
「左右の漸近線が一致するとき」→【例2-1】
があります．ただし，高校では１つのxに対して２つ以上のyを対応させる多価関数のようなものは考えないので，右向きに１つ漸近線があれば他の漸近線はありません．左向きについても同様です．→【図10】「両方とも存在して別のものになるとき」→【例2-2】 「一方だけが存在するとき」→【例2-3】 「１つもないとき」→【例2-4】 【例2-1】 y= 1x2+1の関数ではx→∞のとき分母が∞となってy→0です． x→−∞のときも分母が∞となってy→0となり，左右の漸近線は一致します． ⇒ 漸近線の方程式はy=0（図６） 【例2-2】 y= 11+e−xの関数ではx→∞のときe−∞=0だから分母→1となってy→1です． x→−∞のときはe∞→∞だから分母が∞となってy→0となり，左右の漸近線は一致しません． ⇒ 漸近線は左右で異なり，各々y=0, y=1です．（図７） 【例2-3】 y=xexの関数では x→∞のときy→∞となって漸近線はありません． x→−∞のときはx=−sとおくとxex=−se−s=−  ses→0
となってy=0が漸近線です．⇒ 漸近線は左側だけにありy=0です．（図８） 【例2-4】 y=x2の関数では x→∞のときy→∞となって漸近線はありません． x→−∞のときもy→∞となって漸近線はありません． ⇒ 漸近線は左右いずれもありません．（図９）
|
次の極限は，すぐに使えるようにしておきましょう．（証明はロピタルの定理を使って行うとよい．）
(1)x→∞のときexはxよりも強い．
xex→0，
exx→∞(2)x→∞のときlog xはxよりも弱い． xlogx→∞，
logxx→0 |
|
(3)斜め方向の（y=ax+bの形の）漸近線
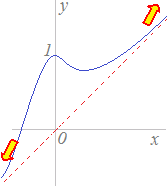
(2)のときと同様，左右各々漸近線を考えることができます．また，(2)と同様にして右向きに１つ漸近線があれば他の漸近線はありません．左向きについても同様です．x→±∞のとき|y−(ax+b)|→0になるとき，y=ax+bが漸近線になります． さらに，右向きについてy=aの形の漸近線があればy=ax+bの形の漸近線はなく，逆も言えます．左向きも同様です．  【例3-1】 y= 2x2+x−2x−1の斜め方向の漸近線を求めるには(1) yx=2x2+x−2x2−x=2+1/x−2/x21−1/x→2（最高次の項［係数は付けても付けなくてもよい］で割って極限を求めます．） (2) (1)で求めた2の値を使って y−2x= 2x2+x−2x−1−2x=2x2+x−2−2x2+2xx−1=3x−2x−1= 3−2/x1−1/x→3⇒ 漸近線の方程式はy=2x+3（図11） （なお，この曲線には縦方向の漸近線x=1もあります．） 【例3-2】 y= x3+1x2+1の斜め方向の漸近線を求めるには(1) yx=x3+1x3+x=1+2/x31+1/x2→1（最高次の項で割って極限を求めます．） (2) (1)で求めた1の値を使って y−1x= x3+1x2+1−x=x3+1−x3−xx2+1=−x+1x2+1→0⇒ 漸近線の方程式はy=1x（図12）
【全体のまとめ】
(1)縦方向の漸近線があれば求める． （分母が0になる場合が多い）
(2)横方向の漸近線があれば求める．
(3)右左各々について
横方向があれば斜め方向はない．
横方向がないとき斜め方向の可能性を考える． 斜め方向も１本あれば他の斜め方向はない． |
y=ax+bの形の漸近線を求めるためには，(1) 初めにaを求め，(2)そのaを使ってbを求めます．逆順は無理です.
(1)初めにaを求めます．
y→ax+bとなるときは，
(2)次にbを求めます．
yx→ax+bx=a+bx→aとなるはずです． そこで，まず yxの極限を求めて，極限値があればこれをaとおきます．（極限値が有限確定でなければこの形の漸近線はないということです．）
y→ax+bとなるときは，y−ax→bとなるはずです．
そこで，(1)で求めたaを使って，y−axの極限を求めて，極限値があればこれをbとおきます．（極限値が有限確定でなければこの形の漸近線はないということです．）
高校では，漸近線として直線だけを考えます．次の図13は
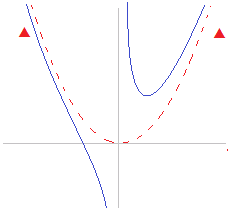
y=x2+ 1xのグラフで，y=x2に限りなく近づきますが，高校では２次式以上の漸近線は扱いません．
|
|
○次の関数を順に選んで下の問題を解いてください．（表示色⇒［現在選択されている問題］［完了した問題］）
（この頁では，コンピュータで描いたグラフをヒントとして使います．） (1)y= 1(x+1)(x−2)
(2)y=x(x+1)(x−2)
(3)y=x(x−3)(x+1)(x−2)
(4)y=(x+2)x(x−3)(x+1)(x−2)(5)y= 2x2+1
(6)y=2xx2+x+1
(7)y=2x2−3x+1x2−x+1
(8)y=2x3−3x2+x+4x2+1(9)y=tanx(−π≦x≦π) (10)y=cos 1x
(11)y=11−ex
(12)y=sinxx(13)y=2x−3ex (14)y=x+logx |
|
|
|
（y軸方向のスケールは，必要に応じて拡大縮小されています．）
 
5
−5
|