■漸近線の方程式

◇解説◇

　高校の微分積分で漸近線の問題が登場するのは，微分法の応用として，「増減，極値，凹凸，変曲点，漸近線の方程式を求めてグラフの概形を書け」という場面です。
　したがって，漸近線の方程式を単独で問うことはまれです。

　漸近線とは，一言で言えば「ある曲線が限りなく近づく相手方の線」のことですが，高校数学で漸近線と言えば「直線」に限ります(*)。したがって，高校数学の漸近線は

　(A)縦線：「ｘ軸に垂直な直線 ( x=a の形のもの)」
　(B)斜め線：「y = ax+b の形のもの (a=0の場合:横線を含む)」

の２種類だけです。
(*)　高校数学では，直線以外の漸近線は考えません。

例えば曲線y = x2+は  ｘ→±∞において y = x2 に限りなく近づきますが，高校では漸近線として y = x2 を求める必要はありません。この例では, 縦線：x = 0 だけが漸近線です。

◎(A)「縦」の漸近線の求め方

有限の値 a に対して，
f(x) = ∞ または −∞

f(x) = ∞ または −∞
となるとき(一方だけでもよい)， x = a が漸近線です．
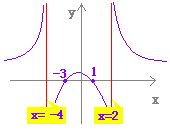
　この形の漸近線は，「分母が0となるｘの値」を探せばほとんど見つかります。(　y = tan x における x = のように「潜んでいるもの」もあります。) 		例

y =

で分母が0となるxの値は 2, -4 です。
→「縦」の漸近線の方程式は x = 2 および x = -4 です。
(x = 1 , x = -3 は漸近線ではなく，ｘ軸との交点です．)

(B)「斜め又は横」の漸近線

x → +∞ のとき y = ax+b が漸近線であるとは，
{f(x) -(ax+b)} = 0･･･(1)

となることです。この条件を満たすa, b の値は，２段階に分けて求められます．
(1)が成り立つならば当然

{−a−} = 0 ･･･(2)は必要条件

したがって，
= a ･･･(2)’


その求めた a の値を用いて，
{f(x)−ax} = b ･･･(3)


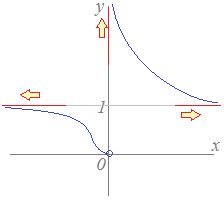
x → -∞ のときも同様にして求めます． 　|･･･(続き)･･･＞ 		◎(B)「斜め又は横」の漸近線の求め方(まとめ)

1) 　 = a　とする。(a = 0 のときはx軸に平行)
この極限がなければ，x → ∞ のとき漸近線なし。

2) 　1)の極限値が存在するとき，a の値を用いて，
{f(x)−ax} = b とする．
※　横(x軸に平行)の漸近線は，直ちに見つかることがあります。

例　y = e−x2のとき e−x2 = 0だから y = 0 は漸近線です．

上の議論で a = 0, b= 0 です。
※　(y = ±f(x) のように初めから曲線が２つあるような場合は論外として) 横の漸近線があれば斜めの漸近線はありません．


(例1)
y = 		◇x軸に垂直な漸近線◇
　x = 0, 1 のとき分母が 0 となり，分子は0とならない．

　 = ± ∞， = ± ∞　だから

　漸近線の方程式は x = 0, 1　･･･　答
◇x→±∞のときの漸近線◇
　　 = 1 　だから，漸近線の方程式は y = 1　･･･　答
(例2)
y = 		◇x軸に垂直な漸近線◇
　x = ± 1 のとき分母が 0 となり，分子は0とならない．

　 = ± ∞， = ± ∞　だから

　漸近線の方程式は x = ± 1　･･･　答
◇x→±∞のときの漸近線◇

　 = 2

　 { −2x} = = = 0

　だから，漸近線の方程式は y = 2x　･･･　答
(例3)
y = e
◇x軸に垂直な漸近線◇
　x = 0 のとき指数の分母が 0 となり，

　e = ∞　･･･　ア

　e = 0　･･･　イ

　アより漸近線の方程式は x = 0　･･･　答 　(イは漸近線とはならない)
◇x→±∞のときの漸近線◇

　e = 1

　だから，漸近線の方程式は y = 1　･･･　答

■　問題　次の曲線の漸近線の方程式を求めなさい。(なお，空欄にはスペースを使わずに半角の「アルファベット小文字または数字」だけを使用するものとします．)
問題 答案
(1)
y = x+
◇x軸に垂直な漸近線◇
　なし
◇x→±∞のときの漸近線◇
　だから，x → ∞ のとき，漸近線の方程式は y = 　･･･　答

　次に，x → －∞ のとき，漸近線の方程式を求める．
　だから，x → -∞ のとき，漸近線の方程式は y = 　･･･　答
(2)
y =
◇x軸に垂直な漸近線◇
　だから漸近線の方程式は x =−, x = 　･･･　答
◇x→±∞のときの漸近線◇

　だから，漸近線の方程式は y = 　･･･　答
(3)
y =
◇x軸に垂直な漸近線◇
だから，漸近線の方程式は x = 　･･･　答

◇x→±∞のときの漸近線◇

だから，x → +∞ のとき，漸近線の方程式は，y = 　･･･答

次に，x → −∞ のとき，漸近線の方程式を求める．


だから，x → −∞ のとき，漸近線の方程式は，y = 　･･･答
(4)
y =
◇x軸に垂直な漸近線◇

だから，漸近線の方程式は x = 　･･･　答

◇x→±∞のときの漸近線◇

だから，x → ±∞ のとき，漸近線の方程式は，y = 　･･･答

 ◇短縮答案◇

■［個別の頁からの質問に対する回答］[漸近線の方程式について／16.12.24］
わかりやすい説明で概要を掴めますがいざ実践してみるとなかなかできないものです。 なので簡単な問題がその後に付属して実戦形式で行えるのは良かったと思います。 それによって理解が深まった気がします。
＝＞［作者］：連絡ありがとう．筆者の苦労が込められているという点からいえば増減.極値.凹凸.変曲点.漸近線.グラフの方もお勧めしたいところです．
...メニューに戻る