|
■解説
(解説1) 右図(1)の対数の定義を用いた解説:   |
このページの「マイナーチェンジありカバー版」「パソコン用」ページ
(グーグルブロガー版)は,こちら⇒ ◆基本事項の確認◆ ○ 対数の定義 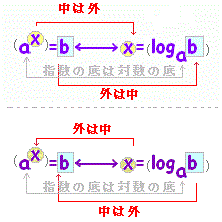 ・・・(1) ・・・(1)○ 対数の計算法則  ・・・(3) ・・・(3)
指数が対数のときに,簡単になるのは底が同じときです。  底が異なれば,このように簡単になるとは限りません。(下の例題1参照)
logaax = x |
|
■解説
(解説1) 右図(1)の対数の定義を用いた解説:   |
このページの「マイナーチェンジありカバー版」「パソコン用」ページ
(グーグルブロガー版)は,こちら⇒ ◆基本事項の確認◆ ○ 対数の定義  ・・・(1) ・・・(1)○ 対数の計算法則  ・・・(3) ・・・(3)
指数が対数のときに,簡単になるのは底が同じときです。  底が異なれば,このように簡単になるとは限りません。(下の例題1参照)
logaax = x |
| 例題1
(答案例) 両辺について底cの対数をとると 
右辺→  |
例題2 次の各式を簡単にしなさい。
(1) 10log103 (2) 5-log53 (答案例)
|
|
|
 |
上の要点参照
2log23x=3x  23+log2x=2log28+log2x=2log28x=8x
別解 23+log2x=232log2x=8・2log2x=8x 上の例題1参照
log2(xlog23)=log23・log2x log2(3log2x)=log2x・log23 これらは等しいから( )内も等しい xlog23=3log2x  |
|
■問題2 各々正しいものをクリック
(1)
解説やり直す に注意して変形することを考えます 選択肢の方は 等しいのは
(2)
解説やり直す
底の変換公式
に注意して,問題の指数を変形しておくと楽です だから |
(3)
解説やり直す
負の指数についての,次の公式
を使って,元の問題を変形しておくと楽です |
|
■[個別の頁からの質問に対する回答][指数が対数のものについて/16.11.4]
一番難しい例題1のところが見ても読んでもさっぱりわからない。どれだけ紙に書いて計算しようとしても意味がわからず筆が一切動かない
=>[作者]:連絡ありがとう.その頁は指数も対数もどちらも理解していないとできません.頁の先頭にあるサブメニューをたどって,基本の定義を理解してから読み直すとよいでしょう.・・・教材の順序から推定すれば,おそらく対数の定義がまだ十分身に付いていない可能性があります. |