maximaの初歩的な操作17･･･関数のフーリエ級数展開

== maximaの初歩的な操作17 ==
･･･関数のフーリエ級数展開･･･
○Xmaxima，wxMaxima のインストール方法，基本操作については［この頁］参照

○wxMaximaでフーリエ級数を扱うには

メニューから［数値処理］→［自動的に数値で出力］などのコマンドを１つ実行して，(%i1)という入力行，(%o1)という出力行を１つ出します．

これ以降に登場するコマンドでフーリエに対応する綴りがfourierとなるのに対して，最初にロードするパッケージの名前はfourieとなることが注意点

次に，(%i1)の行を次のように書き換えて，フーリエ級数を扱うためのパッケージをロードします．
load(fourie);
これにより，以下に述べる
totalfourier (f, x, p);
という関数が使えるようになります．

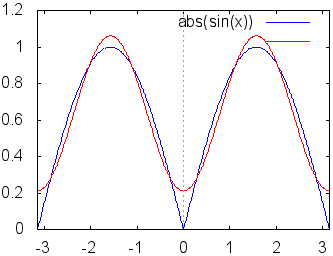
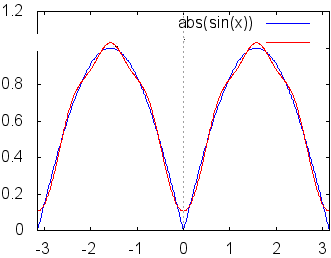
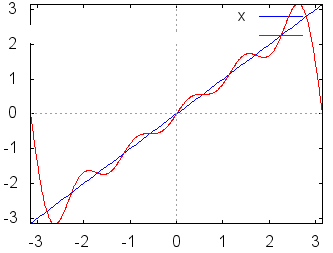
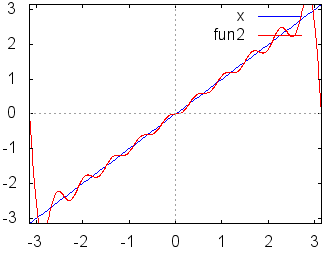
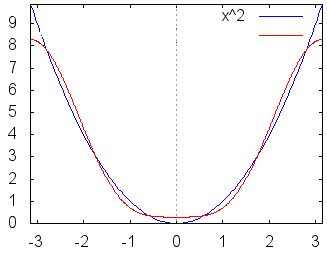
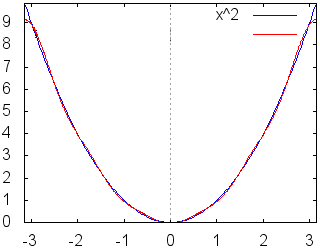
【フーリエ級数の短い解説】
○区間[ −π, π]において
$f(x)=a_0+ (a_1 \cos x + b_1 \sin x) +(a_2 \cos 2x + b_2 \sin 2x)$
$+(a_3 \cos 3x + b_3 \sin 3x) + \cdots$ …(A)

で表される関数を考えると，各々の係数 $a_n$ ， $b_n$ は
$a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nx dx$ …(B)
$b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nx dx$ …(C)
に等しい．
ただし
$a_0=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x) dx$
$b_0=0$ とする．
(A)をフーリエ級数，(B)(C)をフーリエ係数という．

他の $a_n(n\geq 1)$ との整合性を考えて $a_0$ の代わりに $\frac{a_0}{2}$ を使うことが多い． $a_0$ の値が２倍だけ合わないと思うときは，どちらの定義で書かれているかを確かめるとよい．ただし，展開式にすれば同じものになる．

○上記の性質は，区間[ −π, π]における三角関数の直交性から導かれる．

任意の正の整数nについて
$\int_{-\pi}^{\pi}\cos nx dx=0$ …(1)
$\int_{-\pi}^{\pi}\sin nx dx=0$ …(2)
つねに
$\int_{-\pi}^{\pi}\cos mx \sin nx dx=0$ …(3)
m≠nのとき
$\int_{-\pi}^{\pi}\cos mx \cos nx dx=0$ …(4)
$\int_{-\pi}^{\pi}\sin mx \sin nx dx=0$ …(5)
m=nのとき
$\int_{-\pi}^{\pi}\cos nx \cos nx dx=\pi$ …(6)
$\int_{-\pi}^{\pi}\sin nx \sin nx dx=\pi$ …(7)

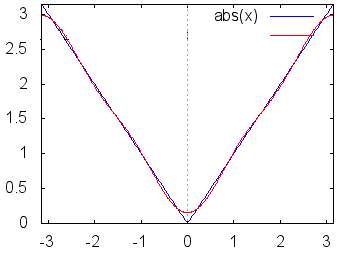
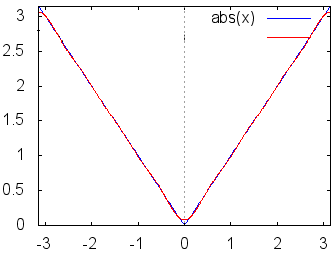
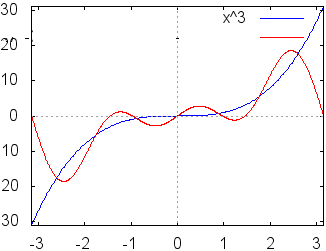
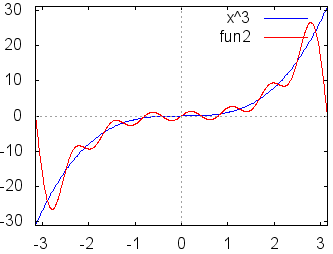
　各々簡単な定積分の計算なので，やってみればわかるがここでは証明は略する．
　これらの性質により，例えばf(x)にcosnxを掛けて区間[ −π, π]において積分すると
（左辺） $=\int_{-\pi}^{\pi}f(x)\cos nx dx$

（右辺） $=\cdots$
$+(a_n \int_{-\pi}^{\pi}\cos nx \cos nx dx$
$+ b_n \int_{-\pi}^{\pi}\sin nx \cos nxdx)+ \cdots$
$\cdots$

ここで赤で示した項は(1)(3)(4)により０となって消える．青で示した項だけが(6)により $a_n \pi$ となって残る．そこで
$a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nx dx$
が成り立つ．
$b_n$ についても同様にして示される．

○与えられた関数，例えばf(x)=x , xnあるいは，音声データや画像データに対して，上記の(B)(C)で求めたフーリエ係数を用いてフーリエ級数(A)を作ると，数学的にはこれが「元の関数f(x)に収束するかどうか」「不連続関数ならどうなるのか」「区間の端の点ではどのように接続されるのか」という難しい問題があるが，この頁ではこのような数学的に厳密な議論には深入りしない．
　むしろ，実用的には「無限」に長い級数を扱うつもりはなく，適当なところで打ち切って「フーリエ多項式」として使いたい．特に，データサイズの大きな音声や画像を完全に再現するのではなく，実用に耐え得る程度に「圧縮」して使いたい．
　このような目的から言えば，フーリエ多項式が「よい近似式」であればそれで十分だといえる．

【wxMaximaを用いて関数のフーリエ級数展開を求める】

関数 $x$ のフーリエ級数展開入力totalfourier(x,x,%pi);

※totalfourier(関数 , 変数 , 区間 )の形で使う
ただし，区間は，−π≦x≦πの場合に%piなどと指定する．（右端の正の値のみ指定）
※HELP情報を見ると，関数totalfourier( )は
fourexpand (foursimp (fourier (f, x, p)), x, p, 'inf)を組み合わせたものとされているが，便利なのでこれを使うとよい．

（結果）

奇関数なので，定数項a0およびcoskxの項はすべて消えます．

$-2\sum_{n=1}^{\infty}\frac{(-1)^{n}sin(nx)}{n}$
すなわち
$2\Bigl(\sin x -\frac{\sin 2x}{2}+ \frac{\sin 3x}{3}- \cdots \Bigr)$ …(1)

※近似の程度を調べるには，［２次元プロット］を用いて
wxplot2d([元の関数, フーリエ多項式], [x,-%pi,%pi], [y,-%pi,%pi]);
を実行すればよい．（cosnx, sinnxまでとった有限数列の和は第ｎ次のフーリエ多項式と呼ばれる．）

青が元の関数，赤がフーリエ多項式のグラフ

第５次まで使った場合第10次まで使った場合

※なお，この頁ではフーリエ級数が元の関数に収束するための条件を示していないが，(1)の無限級数はxに収束するので，例えば $x=\frac{\pi}{2}$ を代入すると
$\frac{\pi}{2}=2\Bigl(\sin \frac{\pi}{2} -\frac{\sin \pi}{2}+ \frac{\sin \frac{3\pi}{2}}{3}- \cdots \Bigr)$
すなわち
$1 - \frac{1}{3}+ \frac{1}{5} - \frac{1}{7} \cdot\cdot\cdot =\frac{\pi}{4}$ …(1’)
が示される．

関数 $x^2$ のフーリエ級数展開入力totalfourier(x^2,x,%pi);

（結果）

偶関数なので，sinkxの項はすべて消えます．

$\frac{\pi^2}{3}+ 4\Bigl(\sum_{n=1}^{\infty}\frac{(-1)^{n}cos(nx)}{n^2} \Bigr)$
すなわち
$\frac{\pi^2}{3} + 4\Bigl(-\frac{\cos x}{1^2} + \frac{\cos 2x}{2^2} - \frac{\cos 3x}{3^2}+ \frac{\cos 4x}{4^2} \cdot\cdot\cdot \Bigr)$ …(2)

青が元の関数，赤がフーリエ多項式のグラフ

第２次まで使った場合第５次まで使った場合

※(2)に $x=\frac{\pi}{2}$ を代入すると
$\frac{\pi^2}{4}=\frac{\pi^2}{3}+ 4\Bigl(-0+ \frac{-1}{2^2}-0 + \frac{1}{4^2}-0 + \frac{-1}{6^2} \cdot\cdot\cdot \Bigr)$
すなわち
$-\frac{\pi^2}{12}= 4\Bigl(- \frac{1}{2^2} + \frac{1}{4^2}- \frac{1}{6^2} \cdot\cdot\cdot \Bigr)$
$-\frac{\pi^2}{48}= - \frac{1}{2^2} + \frac{1}{4^2}- \frac{1}{6^2} \cdot\cdot\cdot$
$\frac{\pi^2}{48}= \frac{1}{4} \Bigl( \frac{1}{1^2} - \frac{1}{2^2}+ \frac{1}{3^2} -\cdot\cdot\cdot \Bigr)$
$\frac{\pi^2}{12}= \frac{1}{1^2} - \frac{1}{2^2}+ \frac{1}{3^2} -\cdot\cdot\cdot$ …(2’)
が示される．

関数 $|x|$ のフーリエ級数展開
入力totalfourier(abs(x),x,%pi);

（結果）

偶関数なので，sinkxの項はすべて消えます．

$\frac{2\Bigl(\sum_{n=1}^{\infty} \frac{((-1)^n-1)cos(nx)}{n^2}\Bigr)}{\pi}+ \frac{\pi}{2}$
すなわち
$\frac{\pi}{2} - \frac{4}{\pi}\Bigl(\frac{\cos x}{1^2} + \frac{\cos 3x}{3^2} + \frac{\cos 5x}{5^2}+ \cdot\cdot\cdot \Bigr)$ …(3)

青が元の関数，赤がフーリエ多項式のグラフ

第３次まで使った場合第７次まで使った場合

※(3)に $x=0$ を代入すると
$0=\frac{\pi}{2}- \frac{4}{\pi}\Bigl( \frac{1}{1^2} + \frac{1}{3^2}+ \frac{1}{5^2} \cdot\cdot\cdot \Bigr)$
すなわち
$\frac{\pi^2}{8}=\frac{1}{1^2} + \frac{1}{3^2}+ \frac{1}{5^2} \cdot\cdot\cdot$ …(3’)
が示される．
さらに，正項級数の和は順序を入れ替えても変わらないという性質を利用すると，次の和も求められる．
$S=\frac{1}{1^2} + \frac{1}{2^2}+ \frac{1}{3^2}+ \frac{1}{4^2} \cdot\cdot\cdot$
とおくと
$S=(\frac{1}{1^2} + \frac{1}{3^2}+ \frac{1}{5^2}+\cdot\cdot\cdot)+(\frac{1}{2^2}+\frac{1}{4^2}+\frac{1}{6^2}+ \cdot\cdot\cdot)$
$=(\frac{1}{1^2} + \frac{1}{3^2}+ \frac{1}{5^2}+\cdot\cdot\cdot)+\frac{1}{4}(\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+ \cdot\cdot\cdot)$
$=(\frac{1}{1^2} + \frac{1}{3^2}+ \frac{1}{5^2}+\cdot\cdot\cdot)+\frac{1}{4}S$
$\frac{3}{4}S=\frac{\pi^2}{8}$
$S=\frac{4\pi^2}{24}=\frac{\pi^2}{6}$ …(3”)

関数 $x^3$ のフーリエ級数展開
入力totalfourier(x^3,x,%pi);

（結果）

奇関数なので，定数項およびcoskxの項はすべて消えます．

$-2\Bigl(\sum_{n=1}^{\infty} \frac{(\pi^2n^2-6)(-1)^n \sin(nx)}{n^3}\Bigr)$
すなわち
$2\Bigl( (\pi^2-6)\sin x - (\frac{\pi^2}{2}-\frac{6}{2^3})\sin 2x + (\frac{\pi^2}{3}-\frac{6}{3^3})\sin 3x- \cdot\cdot\cdot \Bigr)$ …(4)

青が元の関数，赤がフーリエ多項式のグラフ

第３次まで使った場合第７次まで使った場合

関数 $|\sin x|$ のフーリエ級数展開
入力totalfourier(abs(sin(x)),x,%pi);

（結果）

偶関数なので，sinkxの項はすべて消えます．

$\frac{2}{\pi}-\frac{2\Bigl(\sum_{n=1}^{\infty}\frac{((-1)^n + 1)cos(nx)}{(n-1)(n+ 1)} \Bigr)}{\pi}$

　この式は数学の教科書に書かれているものと違う．すなわち，nが偶数の場合だけ上記の項が残り，奇数の場合は０となって消えるはずとなっている．（特にn=1の場合は，分母が０となるので困る．）

　次の式であるはずだと考えられる
$\frac{2}{\pi}-\frac{2\Bigl(\sum_{n=1}^{\infty}\frac{2\cos(2nx)}{(2n-1)(2n+ 1)} \Bigr)}{\pi}$
　すなわち
$\frac{2}{\pi}-\frac{4}{\pi}-4(\frac{\cos 2x}{2^2-1}+ \frac{\cos 4x}{4^2-1}+ \frac{\cos 6x}{6^2-1} \cdot\cdot\cdot)$ …(4)

(4)について青が元の関数，赤がフーリエ多項式のグラフ

第２次まで使った場合第８次まで使った場合

...（携帯版）メニューに戻る

...（PC版）メニューに戻る