絶対値記号２つの外し方

大きな区分

数と式(公式と例)/対称式の変形/実数と根号（公式と例）/根号計算1/根号計算2/分母の有理化/無理数の独立/式の値(無理数の対称式)/xⁿ+1/xⁿの値/センター試験問題平方根の計算/根号計算の入試問題/二重根号/絶対値/絶対値2つの外し方/絶対値の入試問題/文字式を含む根号計算/センター共通数と式問題/

◇絶対値記号の外し方（要点）◇

○
|a| は絶対値記号の中身a の正負によって外れ方が変る．そこで，絶対値記号の中身=0 となる値を境目として，場合分けする．
　　a<0 のとき，|a|=−a
　　0≦a のとき，|a|=a
○
|x−1| は，次のようにx の値で場合分けすれば，絶対値記号を外すことができる．
(1) x<1 のとき，|x−1| =−x+1
(2) x≧1 のとき，|x−1| = x−1
○
　２つの絶対値記号を外すには，３つの区間に場合分けする．
|x+4|+|x−1| は，次のように場合分けすれば，絶対値記号を外すことができる．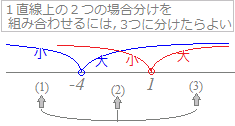

(1) x<−4 のとき，|x+4|+|x−1|=−x−4−x+1=−2x−3
(2) −4≦x<1 のとき，|x+4|+|x−1|= x+4−x+1=5
(3) 1≦x のとき，|x+4|+|x−1|= x+4+x−1=2x+3

◇（参考）２次方程式の解の公式◇

2次方程式 ax²+bx+c=0 (ただし，a≠0 )の解は，

x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}

特に，x の１次の係数が2の倍数のとき，
2次方程式 ax²+2b'x+c=0 (ただし，a≠0 )の解は，

x = \frac{- b^{'} \pm \sqrt{b^{' 2} - a c}}{a}

例えば，2x²+6x+1=0 のときは，a=2 , b'=3 , c=1 として，

x = \frac{- 3 \pm \sqrt{9 - 2}}{2} = \frac{- 3 \pm \sqrt{7}}{2}

半角数字（１バイト文字）で解答すること

ア)　x<−4 のとき，
　　−x−4−x+1=−x2+14
　　x2−2x−17=0
　　x=1±3.

√2√ni
　　x<−4 に適するものはない。 …0個
イ)　−4≦x<1 のとき，
　　x+4−x+1=−x2+14
　　x2=9
　　x=±3
　　−4≦x<1 に適するものは，x=−3 …1個
ウ)　1≦x のとき，
　　x+4+x−1=−x2+14
　　x2+2x−11=0
　　x=−1±2.

√3√ni
　　1≦x に適するものは，x=−1+2.

√3√ni …1個

■［個別の頁からの質問に対する回答］[絶対値記号2つの外し方について／17.2.11］

第5問1≦xのときx2+8x-13=0とありますがx2+9x-13=0ではないでしょうか。
＝＞［作者］：連絡ありがとう．2(3x+1)+3(x−1)=−x2+x+12においてｘの係数は左辺の9だけでなく右辺の１もあるので，これを移項すると８になります．

...メニューに戻る

■このサイト内のGoogle検索■

△このページの先頭に戻る△【アンケート送信】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．

○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）

質問に対する回答の中学版はこの頁，高校版はこの頁にあります